
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема. Численные методы решения задач линейной алгебры,
Лабораторная работа №1 Тема. Решение уравнений. Задание 1. Отделить корни графически и уточнить любой корень с точностью до 0,001 методом деления пополам. № 1. № 3. № 5. № 7. № 9. № 11. № 13. № 15. № 17. № 19. Образец выполнения задания. Найти один корень Перепишем уравнение в виде
Рис. 1 Уточним корень на отрезке [1;2]. Для этого составим таблицу:
Таблица1
Длина последнего отрезка меньше 0,001, поэтому корень приближенно равен его середине, то есть
Задание 2. Отделить корни графически и уточнить с точностью до 0,001 больший корень обоих уравнений методами хорд и Ньютона. № 1. 1) № 2. 1) № 3. 1) № 4. 1) № 5. 1) № 6. 1) № 7. 1) № 8. 1) № 9. 1) № 10. 1) № 11. 1) № 12. 1) № 13. 1) № 14. 1) № 15. 1) № 16. 1) № 17. 1) № 18. 1) № 19. 1) № 20. 1) Образец выполнения задания. Найти один корень Перепишем уравнение в виде
Рис. 2 Уточним корень на отрезке [0;1]. Определим начальную точку Метод хорд. В этом случае Таблица2
Так как | x 5 – x 4| = 0,0001 <0,001, то можно принять Метод касательных. Для этого метода справедливо Таблица 3
Так как | x 3 – x 2| = 0,0004 <0,001, то можно принять
Лабораторная работа №2 Тема. Численные методы решения задач линейной алгебры, Метод Гаусса 1. Решить систему линейных алгебраических уравнений (СЛАУ) 2. Сделать выводы о корректности задачи (существование, единственность, устойчивость решения относительно исходных данных).
Теоретические сведения 1.Система линейных алгебраических уравнений в общем случае имеет вид:
В некоторых случаях эту систему удобнее записывать в матричной форме:
где А - матрица системы,
2. Система (1.1-1.2) имеет единственное решение, если матрица А является невырожденной (detA¹0). 3. Матрицы А и В являются исходными данными и во многих случаях задаются приближенно. Встает вопрос, как погрешности исходных данных влияют на точность решения. Говорят, задача плохо обусловлена, если она чувствительна к малым изменениям входящих в нее исходных данных. В противном случае – хорошо обусловлена. Обусловленность является качественной характеристикой, хотя мы будем стараться оценить ее и количественно, используя величину меры обусловленности
4. Величина
6.Система (1.1-1.2) является хорошо обусловленной, а ее решение – устойчивым, если мера обусловленности 7. Задача решения СЛАУ является корректной, если решение существует и единственно (detA¹0) и устойчиво относительно исходных данных (А и В), т.е. малым изменениям исходных данных соответствуют малые изменения решения задачи. 8. Метод Гаусса (метод последовательного исключения). Суть метода заключается в последовательном исключении неизвестных изсистемы уравнений. Процесс состоит из двух этапов: прямого и обратного ходов. В результате прямого хода система приводится к треугольному виду, а при выполнении обратного хода вычисляются все неизвестные. Образец выполнения задания. Найти решение системы линейных алгебраических уравнений
используя алгоритм метода Гаусса. Введем расширенную матрицу системы, как показано на рис.3 в ячейки А3:D5. Первый этап, приведение матрицы системы к треугольной. 1. Поделим элементы первой строки на а11 .Для этого в ячейку А7 введем формулу А7=А3/A$3$ и скопируем ее вправо до конца строки. 2. Умножим элементы первой строки на (-а21) и прибавим ко 2-ой строке. Для этого введем формулу А8=А7(-А$4$)+А4 и скопируем ее вправо до конца строки. 3. Умножим элементы первой строки на (- а31 ) и прибавим к 3-ей строке. Для этого введем формулу А9=А7(-А$5$)+А5 и скопируем ее вправо до конца строки. Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-й шаг рис.3). 4. Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-ой и3-ей строк (смотри 2-й шаг рис.3).

На этом первый этап метода Гаусса, закончен, матрица системы приведена к треугольной. Второй этап. Здесь последовательно найдем неизвестные, начиная с последней строки. Для этого в ячейки G2:G4 запишем формулы: G4=D13/C13 (для вычисления x 3); G3=D12-C12∙G4 (для вычисления x2); G2=D11-C11∙G4-B11∙G3 (для вычисления x1). Найдем решение исходной системы, используя надстройку Поиск решения. Заготовим таблицу, как показано на рис.4.
Заготовим ячейки А7:С7, где будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например единицы. Эти значения можно рассматривать как нулевое приближение решения системы, 1. Введем коэффициенты системы (матрицу А) в ячейки А3:С5. 2. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейке D 3 введем и скопируем вниз до конца таблицы формулу: D3=СУММПРОИЗВ (A3:C3;$A$7:$C$7). 3. В столбец Е запишем значения правых частей системы. 4. Будет не лишним проверить правильность вычислений для случая 5. Зададим команду Данные\Поиск решения. В окне Параметры поиска решения (рис.5) в поле Изменяя ячейки переменных укажем блок $А$7:$С$7, а в поле Ограничения – $D$3:$D$5 = $E$3:$E$5. Для этого надо щелкнуть на кнопке Добавить и ввести эти ограничения.
Рис. 5 6. Щелкнем на кнопке Найти решение. Полученное решение системы х1 =1; х2 =–1 х3 =2 записано в ячейках А7:С7, рис.4.
Для нахождения обратной матрицы, слева к исходной записываем единичную и аналогичными преобразованиями приводим левую часть к единичной матрице. Для проверки используем функцию МОБР, для вывода всей обратной матрицы выделяем матрицу нужной размерности и нажимаем F 2, Ctrl+Shift+Enter. Находим нормы прямой и обратной матрицы, а также число обусловленности. Для проверки устойчивости придаем правым частям небольшие возмущения и находим решение системы при помощи надстройки Поиск решения.
Лабораторная работа №3 Метод Гаусса-Зейделя Метод Гаусса-Зейделя представляет собой модификацию метода Якоби. Основная идеяметода заключается в том, что при вычислении (k +1)-ой итерации неизвестное
Проиллюстрируем метод для n=3. Пусть система линейных алгебраических уравнений уже приведена к нормальному виду:
Выбираем произвольное начальное приближение
Полученное первое приближение
Используя
Этим заканчивается построение первой итерации
Используя значения первого приближения
Итерационный процесс продолжается до тех пор, пока два соседних приближения
Метод Гаусса-Зейделя. 1. Заготовим таблицу на новом листе Excel как показано на рис.2.4. 2.
В качестве нулевого приближения выберем нулевой вектор  и введем его в ячейки В11:D11. и введем его в ячейки В11:D11.
Рис.8 3. В ячейках В12:D12 запишем формулы для вычисления первого приближения, используя (2.9). Эти формулы имеют вид: B12=$E$6 + B11*$B$6 + C11*$C$6 + D11*$D$6, C12==$E$7 + B12*$B$7 + C11*$C$7 + D11*$D$7, D12==$E$8 + B12*$B$8 + C12*$C$8 + D11*$D$8. 4. В столбце Н сформируем вычисление M(k) , используя выражение, так, как это проделали в предыдущем примере Анализируя результаты, принимаем
Лабораторная работа №4 Численное интегрирование. Задание 1. Вычислить определенный интеграл по формуле средних прямоугольников, используя двойной просчет
Образец выполнения задания. Вычислить определенный интеграл При Таблица 4
Значение интеграла определяем по формуле средних прямоугольников
тогда Аналогично находим значение интеграла при Таблица 5
Значение Задание 2. Вычислить определенный интеграл по формулам трапеций и Симпсона с шагом
Образец выполнения задания. Вычислить интеграл Таблица 6
Тогда по формуле трапеций приближенной значение интеграла
Так как вторая формула более точная, то будем считать Лабораторная работа №7 Транспортная задача На 3-х цементных заводах производится цемент одной и той же марки в количествах соответственно 30, 40, 53 тонн. Цемент следует доставить на четыре завода ЖБК, потребляющих его соответственно в количествах 22, 35, 25, 41 тонн. Стоимости (у.е.) перевозок одной тонны продукта с i -го (i =1,2,3) завода на j -й (j =1,2,3,4) ЖБК приведены в таблице 2. Спланировать перевозки так, чтобы их общая стоимость была минимальной. Таблица 2
Задача о назначениях Имеются три бригады А1, А2, А3, каждая из которых может быть использована на каждом из трех видов работ с производительностью (в условных единицах), заданной в виде табл.5. Таблица 5
Требуется так распределить бригады по одной на каждую из работ, чтобы суммарная производительность всех бригад была максимальной. Распределительная задача Имеется три типа землеройных механизмов: экскаваторы, скреперы, бульдозеры, используемые на двух строительных объектах. Объем землеройных работ на первом строительном объекте равен 12 тыс.м3, на 2-м - 5 тыс.м3. Стоимость машино-смены работы 1-го механизма дана с учетом единовременных затрат на подготовительные работы (доставка, погрузка-разгрузка механизмов, прокладка дорог и проездов и пр.). Производительность i-го механизма на j-ом объекте указана в табл.12. Таблица12
Требуется так распределить механизмы по объектам, чтобы выполнить заданный объем работ с минимальными затратами. Исходные данные для решения задачи приведены в табл.12. 14. Задача оптимального планирования выпуска продукции Завод деревянных конструкций выпускает два основных типа конструкций: А - арки, В - балки (стоимостью 240 и 208 руб./м3 соответственно). Технологический процесс изготовления конструкций состоит из трех основных операций: подготовка пиломатериалов, запрессовка и распрессовка, окончательная обработка. Если рабочее время за год принять за 100%, то затраты времени на каждую операцию можно представить в виде табл.13.
Таблица 13
Следует учесть, что 2-я операция производится на разных прессах разными цехами. Определить оптимальный план выпуска конструкций за год по критерию максимальной прибыли, при условии, что конструкций типа В будет выпущено не более 60%. Лабораторная работа №1 Тема. Решение уравнений. Задание 1. Отделить корни графически и уточнить любой корень с точностью до 0,001 методом деления пополам. № 1. № 3. № 5. № 7. № 9. № 11. № 13. № 15. № 17. № 19. Образец выполнения задания. Найти один корень Перепишем уравнение в виде
Рис. 1 Уточним корень на отрезке [1;2]. Для этого составим таблицу:
Таблица1
Длина последнего отрезка меньше 0,001, поэтому корень приближенно равен его середине, то есть
Задание 2. Отделить корни графически и уточнить с точностью до 0,001 больший корень обоих уравнений методами хорд и Ньютона. № 1. 1) № 2. 1) № 3. 1) № 4. 1) № 5. 1) № 6. 1) № 7. 1) № 8. 1) № 9. 1) № 10. 1) № 11. 1) № 12. 1) № 13. 1) № 14. 1) № 15. 1) № 16. 1) № 17. 1) № 18. 1) № 19. 1) № 20. 1) Образец выполнения задания. Найти один корень Перепишем уравнение в виде
Рис. 2 Уточним корень на отрезке [0;1]. Определим начальную точку Метод хорд. В этом случае Таблица2
Так как | x 5 – x 4| = 0,0001 <0,001, то можно принять Метод касательных. Для этого метода справедливо Таблица 3
Так как | x 3 – x 2| = 0,0004 <0,001, то можно принять
Лабораторная работа №2 Тема. Численные методы решения задач линейной алгебры, Метод Гаусса 1. Решить систему линейных алгебраических уравнений (СЛАУ) 2. Сделать выводы о корректности задачи (существование, единственность, устойчивость решения относительно исходных данных).
|
 ; (кроме х =0) № 2.
; (кроме х =0) № 2.  ;
; ; № 4.
; № 4.  ;
;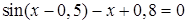 ; № 6.
; № 6.  ;
; № 8.
№ 8. 
 (кроме х =0) № 10.
(кроме х =0) № 10. 
 № 12.
№ 12. 
 № 14.
№ 14. 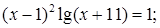
 № 16.
№ 16.  (кроме х =0)
(кроме х =0) № 18.
№ 18. 
 № 20.
№ 20. 
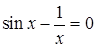 .
. и построим графики левой и правой частей в Excel, изменяя х от 0,5 до 3 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
и построим графики левой и правой частей в Excel, изменяя х от 0,5 до 3 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.


 2)
2) 
 2)
2) 
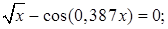 2)
2) 
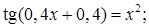 2)
2) 
 2)
2) 
 2)
2) 
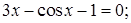 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 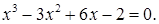
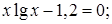 2)
2) 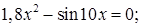 2)
2) 
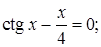 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
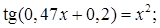 2)
2) 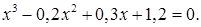

 .
. и построим графики левой и правой частей в Excel, изменяя х от -2 до 2 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
и построим графики левой и правой частей в Excel, изменяя х от -2 до 2 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.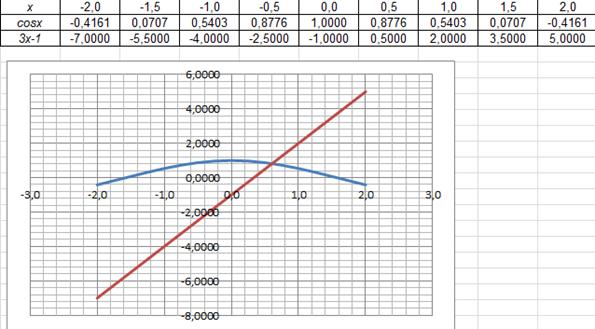
 . В нашем случае
. В нашем случае  , тогда
, тогда  ,
,  на исследуемом отрезке. Так как
на исследуемом отрезке. Так как 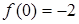 ,
,  , то
, то  , в ней совпадают знаки функции и второй производной.
, в ней совпадают знаки функции и второй производной. , составим вспомогательную таблицу
, составим вспомогательную таблицу
 с точностью
с точностью  .
. , начальная точка выбирается аналогично методу хорд, поэтому удобно воспользоваться следующей таблицей.
, начальная точка выбирается аналогично методу хорд, поэтому удобно воспользоваться следующей таблицей.
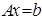 , вычислить определитель и обратную матрицу для матрицы А методом исключения Гаусса. Проверить полученное решение СЛАУ, используя надстройку Excel поиск решения применительно к исходной системе
, вычислить определитель и обратную матрицу для матрицы А методом исключения Гаусса. Проверить полученное решение СЛАУ, используя надстройку Excel поиск решения применительно к исходной системе 
 ,
, ,
, - вектор решения,
- вектор решения,  - вектор свободных членов.
- вектор свободных членов.
 .
. называется нормой матрицы
называется нормой матрицы 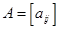 и определяется по одной из 3-х формул:
и определяется по одной из 3-х формул: ;
;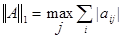 ;
; .
. близка единице.
близка единице.

 .
.
 вычисляется с учетом уже найденных значений
вычисляется с учетом уже найденных значений .
.
 и подставляем в первое уравнение системы
и подставляем в первое уравнение системы
 подставляем во второе уравнение системы (2.8)
подставляем во второе уравнение системы (2.8)
 , находим
, находим  из третьего уравнения
из третьего уравнения
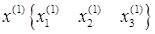
 можно таким же способом построить следующие итерации. Итерацию с номером (k +1) можно представить следующим образом
можно таким же способом построить следующие итерации. Итерацию с номером (k +1) можно представить следующим образом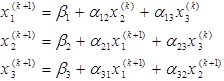
 не станут достаточно близкими. Критерий близости может быть задан так же, как и в методе Якоби.
не станут достаточно близкими. Критерий близости может быть задан так же, как и в методе Якоби.
 за приближенное решение исходной системы с заданной точностью.
за приближенное решение исходной системы с заданной точностью. ,
,  .
. ,
,
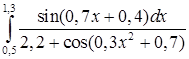 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
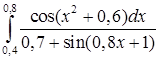 ,
,
 ,
,
 ,
,
 ,
,
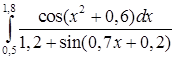 ,
,
 ,
,
 ,
,
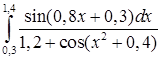 ,
,
 ,
,
 .
.
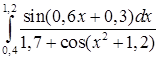 .
. определим шаг
определим шаг  и составим таблицу значений функции в серединах отрезков, оставляя 4 цифры после запятой; находим сумму значений функции.
и составим таблицу значений функции в серединах отрезков, оставляя 4 цифры после запятой; находим сумму значений функции.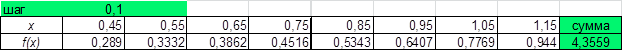
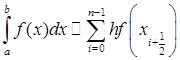 ,
, .
. ,шаг
,шаг 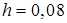 .
.
 . Так как второе значение более точное, то будем считать
. Так как второе значение более точное, то будем считать  .
. .
. ,
,
 ,
,
 ,
,
 ,
,
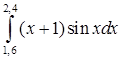 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
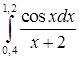 ,
,
 ,
,
 ,
,
 .
.
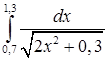 с шагом
с шагом 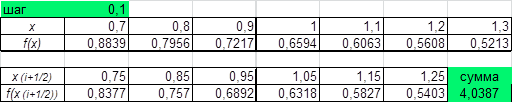
 По формуле Симпсона
По формуле Симпсона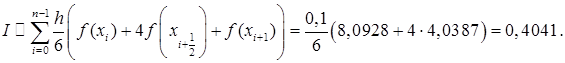
 .
.


