
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы. Линейные операции над матрицамиСодержание книги
Поиск на нашем сайте
Матрицей называется прямоугольная таблица чисел, заключённая в круглые скобки. Если матрица А содержит m строк и n столбцов, говорят, что матрица имеет размерность (или размер) Если строки матрицы заменить столбцами (или, что приведёт к тому же результату, столбцы заменить строками), получится матрица, называемая транспонированной, а сама операция замены строк столбцами (столбцов строками) называется транспонированием и обозначается значком Τ. Если исходная матрица А имеет размерность Если К примеру, если Очевидно, что повторное транспонирование даёт исходную матрицу, то есть (А Τ)Τ= А. Матрица размерности При транспонировании матрицы-столбца получается матрица-строка и наоборот. в целях экономии места матрицу-столбец часто представляют как транспонированную матрицу-строку Упорядоченный набор n чисел Алгебраический вектор называется ненулевым, если хотя бы одна из его компонент отлична от нуля. Нулевой вектор состоит только из нулей. Если число строк матрицы совпадает с числом её столбцов, матрица называется квадратной. Матрица А размерности Элемент квадратной матрицы называется диагональным, если номер его строки совпадает с номером его столбца. Совокупность диагональных элементов называются главной диагональю квадратной матрицы. Квадратная матрица называется треугольно й, если все её диагональные элементы отличны от нуля, а элементы, расположенные под главной диагональю, равны нулю.
Квадратная матрица А называется симметричной, если её элементы, симметрично расположенные относительно главной диагонали, равны, то есть если ai j = a j i. Симметричная матрица не изменяется при транспонировании, А Τ =А. Приведём примеры треугольной и симметричной матриц. Матрица
Матрицы одной размерности можно складывать. Матрицы складываются поэлементно. Умножение матрицы на число определяется как умножение на это число всех её элементов. Поясним правила сложения матриц и умножения матрицы на число примером.
Сложение и умножение на число называются линейными операциями. Умножение матриц Операция умножения определяется не для всяких двух матриц. две матрицы можно перемножить только в том случае, если число столбцов одной матрицы совпадает с числом строк другой. О п р е д е л е н и е. Пусть m ´ k – размерность матрицы А, а k ´ n – размерность матрицы В. Произведением матрицы А на матрицу В называется матрица С (С = АВ) размерности m ´ n, элементы ci j которой вычисляются по формуле
где Сформулируем правило умножения матриц словесно. Чтобы вычислить элемент произведения двух матриц, стоящий на пересечении i -й строки и j -го столбца, нужно элементы i- й строки первой матрицы умножить на соответствующие элементы j- го столбца второй матрицы и полученные произведения сложить. Условная схема умножения матриц такова: (® ¯). Первая стрелка показывает направление перемещения по строкам первой матрицы, вторая – по столбцам второй. Отметим, что произведение матриц содержит столько же строк, сколько первая матрица, и столько же столбцов, сколько вторая. В частности, при умножении матрицы-строки на какую-нибудь другую матрицу получается матрица-строка. Если же какая-то матрица умножается на матрицу-столбец, получается матрица-столбец. При умножении матрицы-строки на матрицу-столбец получается матрица размерности 1×1, то есть число. При умножении квадратных матриц одной размерности получается квадратная матрица той же размерности. Приведём пример умножения матрицы размерности 4×3 на матрицу размерности 3×2, размерность произведения при этом будет 4×2.
В обратном порядке перемножить эти матрицы нельзя, так как умножение матрицы размерности 3×2 на матрицу размерности 4×3 не определено. Покажем, что от перемены мест сомножителей, даже если умножение в обратном порядке возможно, результат может измениться. Если Но Транспонирование произведения двух матриц можно заменить умножением транспонированных сомножителей в обратном порядке, то есть имеет место равенство (AB)Τ = B Τ A Τ. Это равенство пригодится нам при изучении квадратичных форм. Его справедливость легко обосновать. Элемент матрицы B Τ A Τ, стоящий на пересечении i- й строки и j -го столбца, получается как сумма произведений элементов i- й строки матрицы B Τ, то есть i- го столбца матрицы B, на соответствующие элементы j -го столбца матрицы A Τ, то есть j -й строки матрицы A. Именно таким образом вычисляется элемент матрицы AB, стоящий на пересечении j -й строки и i- го столбца и совпадающий с элементом матрицы (AB)Τ, стоящим на пересечении i- й строки и j -го столбца. Квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы – нули, называется единичной и обозначается через E (или через En, если необходимо указать её порядок). Единичные матрицы обладают замечательным свойством: умножение матрицы (слева или справа) на единичную матрицу подходящей размерности не изменяет исходную матрицу. Иными словами, если матрица А имеет размерность Например, Матрица, обозначаемая через A –1, называется обратной по отношению к квадратной матрице A, если верны равенства: AA –1= E и A –1 A = E. Условие, при котором квадратная матрица имеет обратную, содержит понятие определителя квадратной матрицы.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.0.34 (0.008 с.) |

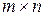 . Элементы матрицы А, обозначаются обычно одноимённой маленькой буквой, снабжённой двумя индексами (номерами) по следующему правилу: элемент, стоящий на пересечении строки с номером i и столбца с номером j, обозначается через
. Элементы матрицы А, обозначаются обычно одноимённой маленькой буквой, снабжённой двумя индексами (номерами) по следующему правилу: элемент, стоящий на пересечении строки с номером i и столбца с номером j, обозначается через 
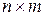 .
. , то
, то  , и
, и  .
. , то
, то  .
. имеет вид
имеет вид  и называется матрицей-строкой (элементы матрицы-строки иногда отделяют друг от друга запятой, возможна запись
и называется матрицей-строкой (элементы матрицы-строки иногда отделяют друг от друга запятой, возможна запись  ). матрицей-столбцом называется матрица вида
). матрицей-столбцом называется матрица вида  , её размерность
, её размерность  .
. .
. называется n- мерным алгебраическим вектором. Эти числа (компоненты вектора) можно расположить в строчку или в столбик. В первом случае получим матрицу-строку
называется n- мерным алгебраическим вектором. Эти числа (компоненты вектора) можно расположить в строчку или в столбик. В первом случае получим матрицу-строку  , во втором – матрицу-столбец
, во втором – матрицу-столбец  называется квадратной матрицей n - го порядка.
называется квадратной матрицей n - го порядка. треугольная, матрица
треугольная, матрица  симметричная.
симметричная. .
. ,
, – элементы i- й строки матрицы А, а
– элементы i- й строки матрицы А, а  – элементы j -го столбца матрицы В.
– элементы j -го столбца матрицы В.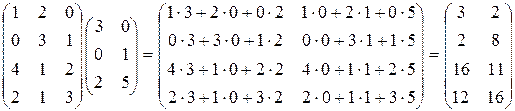
 ,
,  , то
, то 


 .
. . Как видно,
. Как видно,  , то есть умножение матриц не обладает свойством коммутативности.
, то есть умножение матриц не обладает свойством коммутативности. .
. ,
,  .
.


