
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кандидат физико-математических наук, доцент В. Е. Алексеева,Содержание книги
Поиск на нашем сайте
РОССИЙСКОЙ ФЕДЕРАЦИИ ––––––––––––– Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С. М. Кирова» ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Кафедра высшей математики
линейная АЛГЕБРА
Программа курса, контрольные задания и методические указания для студентов заочного отделения ФЭУ (специальность 080100 «Экономика»)
Санкт-Петербург Рассмотрены и рекомендованы к изданию учебно-методической комиссией лесоинженерного факультета Санкт-Петербургского государственного лесотехнического университета я 2012 г.
С о с т а в и т е л ь Кандидат физико-математических наук, доцент В. Е. Алексеева,
О т в. р е д а к т о р кандидат технических наук, доцент Р е ц е н з е н т Кафедра высшей математики СПбГЛТУ
Линейная алгебра: методические указания / сост.: В. Е. Алексеева. – СПб.: СПбГЛТУ, 2012. – 56 с.
В методических указаниях даны программа курса, теоретический минимум, контрольные задания и методические указания по их выполнению. Темплан 2012 г. Изд. № Предисловие линейная алгебра – одна из математических дисциплин, изучаемых студентами специальности 080100 факультета экономики и управления. Изучение линейной алгебры является важной составляющей математического образования бакалавра, специализирующегося по экономике, поскольку на этой дисциплине базируется моделирование многих экономических процессов. Главная задача дисциплины – дать студентам возможность применять методы линейной алгебры в оптимизационных математических моделях экономики. Данное методическое руководство имеет целью помочь студенту справиться с трудностями, возникающими при заочном изучении курса линейной алгебры. Поэтому, наряду с контрольными заданиями, даются методические указания по их выполнению, а также программа курса и необходимый для решения задач теоретический материал. Этот материал может быть полезен и для студентов дневного отделения, изучающих линейную алгебру, поскольку приведённый здесь теоретический минимум изложен логически связно, причём важные для понимания сути дела утверждения снабжены доказательствами.
В силу необходимости сделать предлагаемое руководство кратким, исключены из рассмотрения таких вопросы, как мнимые собственные числа, кратные корни характеристических многочленов, ортогонализацией базиса, критерий Сильвестра; в упрощённо-обзорном изложении, только как приложение к курсу линейной алгебры, даётся тема «Элементы аналитической геометрии». Усвоив приведённые здесь первоначальные сведения из линейной алгебры, можно пополнить свои знания по данному предмету самостоятельно. Контрольные задания составлены таким образом, что вычислительную работу, выполненную при решении одной задачи, можно использовать при решении следующих задач. Это позволяет сосредоточиться на главном. При выполнении контрольных работ студент должен руководствоваться следующими правилами. Из каждой десятки задач контрольных заданий нужно решить только ту задачу, номер которой заканчивается той же цифрой, что и номер зачётки. Перед решением каждой задачи нужно указать её номер и полностью привести условие. Контрольные работы выполняются в обычной школьной тетради. На обложке тетради, кроме фамилии, имени и отчества, пишут название факультета, номер зачётной книжки, номер специальности, курс, форму обучения (полную или сокращённую), а также номер контрольной работы. В той же тетради выполняется работа над ошибками. В работе над ошибками должны быть представлены только те фрагменты решения, в которых была допущена ошибка. Программа курса «Линейная алгебра» Тема 1. Матрицы, определители, системы линейных уравнений. Матрицы. Линейные операции над матрицами. Умножение матриц. Определители и их свойства. Решение систем линейных уравнений по формулам Крамера. Обратная матрица. Матричный метод решения систем линейных уравнений. Решение систем линейных уравнений методом Гаусса. Ранг матрицы. Теорема Кронекера-Капелли. Тема 2. Линейное пространство. Определение линейного пространства. Линейно независимые векторы. Базис линейного пространства. Собственные числа и собственные векторы квадратной матрицы.
Линейные операторы. Тема 3. Элементы аналитической геометрии Декартова система координат на плоскости. Прямая на плоскости. Векторы. Линейные операции над векторами. Декартова система координат в пространстве. Координаты вектора. Скалярное произведение векторов. Коллинеарность и перпендикулярность векторов. Прямая и плоскость в пространстве. Тема 4. Квадратичные формы. Квадратичная форма. Матричное представление квадратичной формы. Положительно и отрицательно определённые квадратичные формы. Приведение квадратичной формы к каноническому виду.
Т е о р е т и ч е с к и й м и н и м у м Матрицы и определители Умножение матриц Операция умножения определяется не для всяких двух матриц. две матрицы можно перемножить только в том случае, если число столбцов одной матрицы совпадает с числом строк другой. О п р е д е л е н и е. Пусть m ´ k – размерность матрицы А, а k ´ n – размерность матрицы В. Произведением матрицы А на матрицу В называется матрица С (С = АВ) размерности m ´ n, элементы ci j которой вычисляются по формуле
где Сформулируем правило умножения матриц словесно. Чтобы вычислить элемент произведения двух матриц, стоящий на пересечении i -й строки и j -го столбца, нужно элементы i- й строки первой матрицы умножить на соответствующие элементы j- го столбца второй матрицы и полученные произведения сложить. Условная схема умножения матриц такова: (® ¯). Первая стрелка показывает направление перемещения по строкам первой матрицы, вторая – по столбцам второй. Отметим, что произведение матриц содержит столько же строк, сколько первая матрица, и столько же столбцов, сколько вторая. В частности, при умножении матрицы-строки на какую-нибудь другую матрицу получается матрица-строка. Если же какая-то матрица умножается на матрицу-столбец, получается матрица-столбец. При умножении матрицы-строки на матрицу-столбец получается матрица размерности 1×1, то есть число. При умножении квадратных матриц одной размерности получается квадратная матрица той же размерности. Приведём пример умножения матрицы размерности 4×3 на матрицу размерности 3×2, размерность произведения при этом будет 4×2.
В обратном порядке перемножить эти матрицы нельзя, так как умножение матрицы размерности 3×2 на матрицу размерности 4×3 не определено. Покажем, что от перемены мест сомножителей, даже если умножение в обратном порядке возможно, результат может измениться. Если Но Транспонирование произведения двух матриц можно заменить умножением транспонированных сомножителей в обратном порядке, то есть имеет место равенство (AB)Τ = B Τ A Τ. Это равенство пригодится нам при изучении квадратичных форм. Его справедливость легко обосновать. Элемент матрицы B Τ A Τ, стоящий на пересечении i- й строки и j -го столбца, получается как сумма произведений элементов i- й строки матрицы B Τ, то есть i- го столбца матрицы B, на соответствующие элементы j -го столбца матрицы A Τ, то есть j -й строки матрицы A. Именно таким образом вычисляется элемент матрицы AB, стоящий на пересечении j -й строки и i- го столбца и совпадающий с элементом матрицы (AB)Τ, стоящим на пересечении i- й строки и j -го столбца.
Квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы – нули, называется единичной и обозначается через E (или через En, если необходимо указать её порядок). Единичные матрицы обладают замечательным свойством: умножение матрицы (слева или справа) на единичную матрицу подходящей размерности не изменяет исходную матрицу. Иными словами, если матрица А имеет размерность Например, Матрица, обозначаемая через A –1, называется обратной по отношению к квадратной матрице A, если верны равенства: AA –1= E и A –1 A = E. Условие, при котором квадратная матрица имеет обратную, содержит понятие определителя квадратной матрицы. Свойства определителей 1. Определитель, содержащий строку, состоящую из нулей, равен нулю. 2. Определитель, содержащий две одинаковые строки, равен нулю. 3. При перестановке двух строк определитель меняет знак. 4. Если элементы какой-нибудь строки определителя имеют общий множитель, его можно вынести за знак определителя. 5. Определитель, содержащий две пропорциональные строки, равен нулю. 6. Если каждый элемент какой-нибудь строки определителя представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, в соответствующих строках которых стоят: в одном из них первые слагаемые, в другом – вторые. 7. Определитель не изменится, если к какой-нибудь его строке прибавить другую строку, умноженную на какое-нибудь число. 8. Cумма произведений элементов какой-нибудь его строки на алгебраические дополнения элементов другой строки равна нулю. аналогичные свойства определителя можно сформулировать для его столбцов. Для определителей второго порядка все свойства легко доказываются непосредственным вычислением. Для определителей третьего порядка доказательства опираются на теорему о разложении по строкам и столбцам. докажем свойства 6, 7 и 8 для определителей третьего порядка. Выпишем шестое свойство:
Свойство 7 состоит в том, что определитель, стоящий в правой части, согласно свойству 6, равен сумме Докажем свойство 8. Сумма произведений элементов третьей строки определителя
строке Квадратная матрица называется невырожденной, если её определитель отличен от нуля, в противном случае она называется вырожденной. Невырожденными, очевидно, являются треугольные и единичные матрицы. Любая невырожденная матрица имеет обратную. Если
Правильность вычисления матрицы A –1 проверяется умножением A на A –1. Выполним эту проверку. AA –1= Поясним, что здесь при вычислении диагональных элементов произведения элементы строк матрицы A умножаются на алгебраические дополнения этих элементов, так что получаются Δ. Когда же вычисляются недиагональные элементы произведения, элементы строки умножаются на «чужие» алгебраические дополнения и, по свойству 8, получаются нули. Формулы Крамера Рассмотрим систему трёх линейных уравнений с тремя неизвестными Если матрица коэффициентов системы не вырождена, то есть
где Аналогичные формулы (мы принимаем их на веру, без доказательства) справедливы для любой системы линейных уравнений с невырожденной матрицей коэффициентов. С л е д с т в и е ф о р м у л К р а м е р а. Если главный определительсистемы линейных уравнений отличен от нуля, то система имеет единственное решение. В частности, если главный определитель системы линейных уравнений, свободные члены которой равны нулю (такая система называется однородной), отличен от нуля, то система имеет единственное нулевое (состоящее из нулей) решение. Так, однородная система Метод Гаусса Универсальным методом решения систем линейных уравнений является метод Гаусса. В отличие от матричного метода и формул Крамера метод Гаусса можно применять для решения любых систем линейных уравнений. Метод Гаусса позволяет также установить, имеет ли система решения (в этом случае она называется совместной) или нет (тогда система называется несовместной). Суть метода Гаусса состоит в последовательном исключении неизвестных при помощи преобразований, не нарушающих равносильности. Напомним, что две системы линейных уравнений называются равносильными, если они имеют одинаковые решения либо каждая из них несовместна. Решая систему линейных уравнений методом Гаусса, преобразования уравнений обычно выполняют в матричной форме, выписывая только коэффициенты при неизвестных и свободные члены. Таким образом, преобразование систем линейных уравнений сводится к преобразованию матриц. Поэтому, прежде чем приступить к описанию собственно метода Гаусса, рассмотрим соответствующие преобразования матриц самих по себе, безотносительно к решению систем линейных уравнений.
Ранг матрицы Число r называется рангом матрицы A ( Иными словами, рангом матрицы называется наивысший порядок отличных от нуля миноров. Ранг матрицы, состоящий из нулей, считается равным нулю. Ранг невырожденной квадратной матрицы n -го порядка равен n. В частности, ранг треугольной матрицы равен её порядку. Ранг матрицы размерности Например, Очевидно, что ранг матрицы не изменяется при транспонировании.
легко найти ранг матрицы, имеющей канонический или почти канонический вид. Очевидно, что ранг такой матрицы равен k. Действительно, единичная матрица даёт нам минор k -го порядка, отличный от нуля, а любой минор (k +1)-го порядка равен нулю, так как содержит строку, состоящую из нулей. приведение матрицы к каноническому или почти каноническому виду – один из способов вычисления её ранга, основанный на следующей теореме. Т е о р е м а. Ранг матрицы не меняется при допустимых преобразованиях. Доказательство[†]. Остановимся на допустимых преобразованиях, связанных со строками (перестановка столбцов рассматривается аналогично перестановке строк). Возьмём какой-нибудь минор преобразуемой матрицы. Если преобразование его не затронуло или в преобразовании участвовали только его строки, то этот минор остаётся таким же, как был, либо равным нулю, либо отличным от нуля. Измениться, в этом смысле, минор может, только если в преобразовании участвовала строка, назовём её действующей, элементы которой в минор не входили. При этом возможны два случая: а) изменяемая строка, была переставлена с действующей; б) к изменяемой строке прибавлена действующая строка, умноженная на число, не равное нулю. Пусть ранг матрицы равен r. Это значит, что она содержит минор r -го порядка, отличный от нуля. Предположим, что этот минор в результате допустимого преобразования стал равным нулю, такое возможно. В случае а) в преобразованной матрице возьмём минор, составленный из строк выделенного нами минора, не затронутых преобразованием, и строки, оказавшейся на месте действующей. Этот минор может отличаться от исходного минора лишь знаком и, следовательно, не равен нулю. В случае б) преобразованный минор, с одной стороны, равен нулю, с другой (в силу шестого свойства) – сумме исходного (не равного нулю) минора и другого минора, отличающегося от первого тем, что элементы изменяемой строки заменены элементами действующей строки, умноженной на число, отличное от нуля. Это значит, что минор преобразованной матрицы, составленный из строк исходного минора, не затронутых преобразованием, и действующей строки, отличен от нуля. И в том, и в другом случае преобразованная матрица обладает минором r -го порядка, отличным от нуля, так что ранг матрицы не уменьшился. Теперь покажем, что все миноры (r +1)-го порядка преобразованной матрицы (так же как и исходной) равны нулю. Предположим, что какой-нибудь минор (r +1)-го порядка исходной матрицы перестал быть равным нулю. В случае а) это означает, что он содержит элементы r строк, не участвующих в перестановке, и часть элементов действующей строки. Но минор с такими строками уже был в исходной матрице и должен был быть равным нулю как минор (r +1)-го порядка, поэтому наше предположение о том, что рассматриваемый минор стал отличным от нуля ошибочно. В случае б) преобразованный минор представляет собой сумму исходного минора и другого минора исходной матрицы, умноженного на число. Оба минора, будучи минорами (r +1)-го порядка, равны нулю, значит, равна нулю и их сумма. Значит, и в этом случае следует признать ошибочность нашего предположения. Таким образом, ранг матрицы не увеличился. Итак, если матрица A при помощи допустимых преобразований, приведена к матрице Вот почему к треугольному виду можно привести только невырожденную матрицу. Пример. Чтобы вычислить ранг матрицы
При помощи понятия «ранг матрицы» можно гораздо короче сформулировать полученные нами ранее условия совместности и несовместности систем линейных уравнений. Рассматривая преобразованную расширенную матрицу Несовместность системы, как мы видели, была связана с тем, что столбец Поскольку матрица Т е о р е м а (Кронекера-Капелли). Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы коэффициентов при неизвестных был равен рангу расширенной матрицы. С использованием понятия ранга матрицы легко также переформулировать условия, при которых однородные системы линейных уравнений имеют либо одно, либо бесконечно много решений. Если ранг матрицы коэффициентов однородной системы линейных уравнений равен числу неизвестных, то система имеет единственное (нулевое) решение, если же ранг этой матрицы меньше числа неизвестных, система имеет бесконечное множество решений (в том числе ненулевые). Из этого следует, что, для того чтобы однородная система линейных уравнений с квадратной матрицей коэффициентов имела ненулевые решения, необходимо и достаточно, чтобы главный определитель этой системы был равным нулю (необходимость этого условия уже была установлена). собственные числа и собственные векторы О п р е д е л е н и е. Ненулевой алгебраический вектор X и число λ называются, соответственно, собственным вектором и собственным числом квадратной матрицы A, если каждому собственному числу λ отвечает бесконечно много собственных векторов, поскольку при умножении собственного вектора на какое-нибудь отличное от нуля число t, получается также собственный вектор, Матричное равенство Для того чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы её главный определитель Уравнение Приведём пример вычисления собственных чисел и собственных векторов квадратной матрицы. Пусть Подставляя последовательно эти числа в систему Если
Пусть Если
Пусть Если
Линейные пространства Множество L называется линейным пространством, если для его элементов определены операции сложения и умножения на число, обладающие следующими свойствами: 1) для любых x и y, принадлежащих L, 2) для любых x, y и z, принадлежащих L, 3) существует элемент, обозначаемый через 4) для каждого x из L существует противоположный элемент, обозначаемый через 5) для каждого x из L умножение на единицу даёт тот же x, то есть 6) для любых чисел α, β и любого x, принадлежащего L, 7) для любых чисел α, β и любого x, принадлежащего L, 8) для любого числа α и любых x и y, принадлежащих L, Ещё два свойства, Для доказательства второго представим Примером линейного пространства может служить множество матриц одинаковой размерности, в том числе множество n -мерных алгебраических векторов. Пусть Элементы Если же можно указать такие, одновременно не равные нулю, коэффициенты Пусть в линейном пространстве L имеются n линейно независимых элементов В этом случае совокупность элементов Представление элемента линейного пространства в виде линейной комбинации базисных элементов называется разложением этого элемента по базису. Координаты элемента x относительно данного базиса определяются однозначно. Действительно, пусть имеется два разложения элемента x по базису, Таким образом, если в n -мерном линейном пространстве L выбран базис, каждому элементу x этого пространства сопоставляется алгебраический вектор X – набор его координат, то есть Рассмотрим условие линейной независимости k элементов n -мерного линейного пространства L. Пусть элементы
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.188 (0.012 с.) |

 ,
, – элементы i- й строки матрицы А, а
– элементы i- й строки матрицы А, а  – элементы j -го столбца матрицы В.
– элементы j -го столбца матрицы В.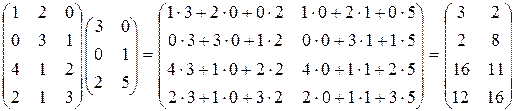
 ,
,  , то
, то 


 .
. . Как видно,
. Как видно,  , то есть умножение матриц не обладает свойством коммутативности.
, то есть умножение матриц не обладает свойством коммутативности. , то
, то  .
. ,
,  .
. . Разложив, каждый из определителей по первой строке, и выполнив элементарные преобразования, убедимся в том, что правая часть равна левой.
. Разложив, каждый из определителей по первой строке, и выполнив элементарные преобразования, убедимся в том, что правая часть равна левой. .
. . По свойству 5 второе слагаемое равно нулю, так как содержит пропорциональные строки. Остаётся первое слагаемое, равное левой части.
. По свойству 5 второе слагаемое равно нулю, так как содержит пропорциональные строки. Остаётся первое слагаемое, равное левой части. на алгебраические дополнения элементов первой строки совпадает с суммой, полученной при разложении по первой
на алгебраические дополнения элементов первой строки совпадает с суммой, полученной при разложении по первой . Эта сумма,
. Эта сумма,  , равна нулю, так как последний определитель (в силу свойства 2) равен нулю. Вместе с ней равен нулю и исходный определитель.
, равна нулю, так как последний определитель (в силу свойства 2) равен нулю. Вместе с ней равен нулю и исходный определитель. =
=  , то обратную матрицу A –1 можно вычислить по следующей формуле (приводим формулу для квадратной матрицы третьего порядка, для квадратных матриц других порядков формулы аналогичны):
, то обратную матрицу A –1 можно вычислить по следующей формуле (приводим формулу для квадратной матрицы третьего порядка, для квадратных матриц других порядков формулы аналогичны): =
=  .
.
 =
= 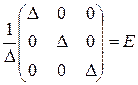 .
. . Определитель Δ =
. Определитель Δ =  , называется главным определителем системы.
, называется главным определителем системы. , то решение системы можно найти по формулам Крамера:
, то решение системы можно найти по формулам Крамера: ,
, ,
,  ,
,  .
. имеет, очевидно, решение
имеет, очевидно, решение  . Оно единственно, если
. Оно единственно, если 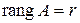 ), если какой-нибудь её минор r -го порядка отличен от нуля, а все миноры (r +1)-го порядка (если они существуют) равны нулю.
), если какой-нибудь её минор r -го порядка отличен от нуля, а все миноры (r +1)-го порядка (если они существуют) равны нулю. и найдётся минор порядка m, отличный от нуля, то ранг матрицы равен m. Если
и найдётся минор порядка m, отличный от нуля, то ранг матрицы равен m. Если  и найдётся минор порядка n, отличный от нуля, ранг матрицы равен n.
и найдётся минор порядка n, отличный от нуля, ранг матрицы равен n. ,
,  ,
,  .
. E
E
 ……..
……..
……..
……..
……..
……..

 0
0

 k n-k
k n-k , ранги этих матриц равны.
, ранги этих матриц равны. , нужно привести её к каноническому или почти каноническому виду. Это было сделано нами на страницах 16 и 17. Были полученные две матрицы:
, нужно привести её к каноническому или почти каноническому виду. Это было сделано нами на страницах 16 и 17. Были полученные две матрицы:  (канонического вида) и
(канонического вида) и 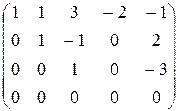 (почти канонического вида). В левом верхнем углу каждой из этих матриц расположена невырожденная квадратная матрица третьего порядка. Все миноры четвёртого порядка равны нулю, так как содержат строку, состоящую из нулей. Значит, ранг всех трёх матриц равен трём.
(почти канонического вида). В левом верхнем углу каждой из этих матриц расположена невырожденная квадратная матрица третьего порядка. Все миноры четвёртого порядка равны нулю, так как содержат строку, состоящую из нулей. Значит, ранг всех трёх матриц равен трём. E
E
 .
.
.
.
.
.
 0
0

 k n-k
k n-k , мы пришли к выводу, что всегда, когда система совместна, матрицы
, мы пришли к выводу, что всегда, когда система совместна, матрицы  имеют канонический вид с одним и тем же единичным (треугольным) блоком порядка k. Поэтому ранги обеих матриц равны k. Так что верно следующее утверждение: если система совместна, то
имеют канонический вид с одним и тем же единичным (треугольным) блоком порядка k. Поэтому ранги обеих матриц равны k. Так что верно следующее утверждение: если система совместна, то  .
. содержал ненулевой элемент
содержал ненулевой элемент  (
( ). С помощью этого элемента можно составить отличный от нуля минор (k +1)-го порядка, присоединив к единичному (треугольному) блоку столбец
). С помощью этого элемента можно составить отличный от нуля минор (k +1)-го порядка, присоединив к единичному (треугольному) блоку столбец 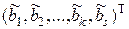 и строку
и строку  . Их общий элемент
. Их общий элемент  станет при этом (k +1)-м диагональным элементом минора. Ясно, что
станет при этом (k +1)-м диагональным элементом минора. Ясно, что 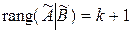 , тогда как
, тогда как  , то есть
, то есть 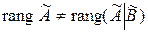 .
. получена из матрицы
получена из матрицы  при помощи допустимых преобразований, сохраняющих ранг матриц и не нарушающих равносильности соответствующих им систем, условия совместности и несовместности преобразованной системы, рассмотренные нами, можно отнести к исходной системе линейных уравнений. Таким образом, справедливо следующее утверждение.
при помощи допустимых преобразований, сохраняющих ранг матриц и не нарушающих равносильности соответствующих им систем, условия совместности и несовместности преобразованной системы, рассмотренные нами, можно отнести к исходной системе линейных уравнений. Таким образом, справедливо следующее утверждение. .
. . Обычно бывает достаточно найти один из них.
. Обычно бывает достаточно найти один из них.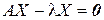 или, что то же самое,
или, что то же самое,  . Вынося за скобки X, получим равенство
. Вынося за скобки X, получим равенство  , которое можно рассматривать как матричную запись однородной системы линейных уравнений.
, которое можно рассматривать как матричную запись однородной системы линейных уравнений.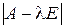 был равен нулю. Значит, число λ будет собственнымчислом матрицы A в том и только в том случае, когда
был равен нулю. Значит, число λ будет собственнымчислом матрицы A в том и только в том случае, когда  , то есть λ должно быть корнем этого уравнения.
, то есть λ должно быть корнем этого уравнения. , тогда
, тогда  – характеристическое уравнение этой матрицы. Вычислив определитель, получим уравнение
– характеристическое уравнение этой матрицы. Вычислив определитель, получим уравнение  , решив которое, найдём, собственные числа
, решив которое, найдём, собственные числа  ,
,  ,
,  .
. ,
,  ,
,  .
. , то
, то 
 и
и  . Решаем систему методом Гаусса.
. Решаем систему методом Гаусса. ~
~  ~
~  ~
~  .
. [‡], тогда
[‡], тогда 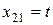 ,
,  , так что
, так что  .
.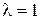 , то
, то  и
и  .
. ~
~  ~
~  ~
~  .
. **, тогда
**, тогда  ,
,  , так что
, так что 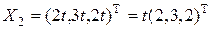 .
. , то
, то  и
и 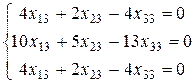 .
.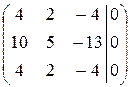 ~
~  ~
~ 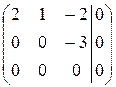 ~
~  . Вторая строка соответствует равенству
. Вторая строка соответствует равенству  , то есть
, то есть  нельзя выбирать произвольно. Пусть
нельзя выбирать произвольно. Пусть  , тогда
, тогда  , так что
, так что  .
. ;
; ;
; , такой, что
, такой, что 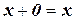 для любого x из L;
для любого x из L; , такой, что
, такой, что  ;
;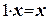 ;
; ;
; ;
; .
. и
и 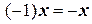 , можно вывести. Покажем это. Из 5) и 7) следует, что
, можно вывести. Покажем это. Из 5) и 7) следует, что  . Тогда
. Тогда  , откуда
, откуда  , то есть
, то есть  . Первое из двух свойств доказано.
. Первое из двух свойств доказано. как
как 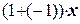 =
=  . Затем, прибавив – x к обеим частям равенства
. Затем, прибавив – x к обеим частям равенства  , откуда
, откуда  и, следовательно,
и, следовательно,  .
. – элементы линейного пространства L. Выражение
– элементы линейного пространства L. Выражение  , где
, где  – какие-то числа, называется линейной комбинацией элементов
– какие-то числа, называется линейной комбинацией элементов  называются линейно независимыми, если из равенства
называются линейно независимыми, если из равенства  следует, что
следует, что  .
. , что соответствующая линейная комбинация обращается в
, что соответствующая линейная комбинация обращается в  , элементы
, элементы 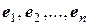 , обладающих тем свойством, что любой элемент x из этого пространства является их линейной комбинацией с коэффициентами
, обладающих тем свойством, что любой элемент x из этого пространства является их линейной комбинацией с коэффициентами  .
. – координатами элемента x относительно этого базиса, число n – размерностью пространства, а само пространство L – n - мерным линейным пространством.
– координатами элемента x относительно этого базиса, число n – размерностью пространства, а само пространство L – n - мерным линейным пространством. и
и  . Вычтем из первого равенства второе. Получим
. Вычтем из первого равенства второе. Получим  . Так как
. Так как  линейно независимы,
линейно независимы,  , следовательно,
, следовательно,  , то есть коэффициенты этих разложений совпадают.
, то есть коэффициенты этих разложений совпадают. . А поскольку при сложении элементов их координаты, очевидно, складываются, а при умножении на число – умножаются на число, элемент x можно отождествить с вектором X. Поэтому линейное пространство часто называют линейным векторным пространством, а его элементы – векторами.
. А поскольку при сложении элементов их координаты, очевидно, складываются, а при умножении на число – умножаются на число, элемент x можно отождествить с вектором X. Поэтому линейное пространство часто называют линейным векторным пространством, а его элементы – векторами. в базисе
в базисе  через
через  (i =1,2,…, k). Предположим, что какая-то линейная комбинация элементов
(i =1,2,…, k). Предположим, что какая-то линейная комбинация элементов  обращается в ноль,
обращается в ноль,  . Поскольку
. Поскольку  должны обращаться в 0. Это значит, что система линейных уравнений относительно неизвестных
должны обращаться в 0. Это значит, что система линейных уравнений относительно неизвестных 


