
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решения в условиях конфликтаСодержание книги Поиск на нашем сайте
Для обоснования решений в условиях конфликта разработаны специальные математические методы, которые рассматриваются в теории игр. Её возникновение относится к 1944г., когда вышла в свет монография Неймана и Моргенштерна «Теория игр и экономическое поведение» [38]. В настоящее время теория игр превратилась в самостоятельное математическое направление, имеющее много практических приложений. В отличие от раздела 1.6, когда параметром z управляла «природа», в условиях конфликта параметр z отражает действия «разумного» противника, преследующего собственные цели. Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций. Необходимость анализировать такие ситуации привела к возникновению теории игр, задачей которой является выработка рекомендаций по рациональному образу действий участников конфликта. В дальнейшем рассматриваются только стратегические игры, в отличие от комбинаторных и азартных игр, когда источник неопределённости состоит в отсутствии информации о действиях противника, о его стратегии. Рассмотрим модель игры более подробно. Если сталкиваются интересы двух противников, игра называется парной, если более двух – множественной. Так как наибольшее практическое значение имеют парные игры, то рассмотрим только их. Итак, участников игры двое – А и В. Задано множество стратегий Х, игроков А и В. Соответственно:
Простейший вид стратегической игры – игра двух лиц с нулевой суммой (сумма выигрышей равна нулю). Выбор стратегии каждым из игроков производится при полном незнании выбора другого игрока. В результате выигрыш
откуда, если
то
Цель игрока А – максимизировать функцию Пусть
Игрок А, не зная информации о выборе стратегии игроком В, должен сделать такой выбор, чтобы максимизировать свой минимальный выигрыш:
где a – гарантированный выигрыш игрока А – называется нижней ценой игры. Стратегия Соответственно игрок В, выбирая стратегию, исходит из следующего принципа: при выборе некоторой стратегии
Величина b называется верхней ценой игры, а соответствующая выигрышу b стратегия Фактический выигрыш игрока А при разумных действиях партнёров ограничен нижней и верхней ценой игры. Если же эти выражения равны
то выигрыш игрока А – вполне определённое число, и игра называется вполне определённой, а выигрыш (1.42) называется решением игры и равен элементу матрицы Вполне определённые игры называются играми с седловой точкой, а элемент Седловой точке соответствует оптимальные стратегии игроков, их совокупность является решением игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии не может быть выгодно.
Пример 1.6
Игры заданы платёжными матрицами:
Для матрицы А1: a 1 = 3, b 1 = 4. Для матрицы А2: a 2 = 2, b 2 = 2. Таким образом, цена второй игры n = 2, решение игры состоит в выборе игроком А стратегии х2, а игроком В – стратегии у2. Легко видеть, что отклонение одним из игроков от оптимальной стратегии приводит к уменьшению выигрыша для игрока А и к увеличению проигрыша для игрока В.
Итак, если игровая матрица содержит седловую точку, то решение игры известно. Возникает вопрос нахождения решения для игр, матрицы которых не содержат седловой точки, в этих играх Естественным для каждого игрока является вопрос увеличения выигрыша (уменьшения проигрыша). Поиски такого решения состоят в том, что игроки применяют не одну, а несколько стратегий, причём выбор стратегий осуществляется случайным образом. Случайный выбор игроком своих стратегий называется смешанной стратегией. В данной игре стратегии игрока А задаются набором вероятностей:
а стратегии игрока В задаются набором вероятностей:
причём: Стратегии игроков А и В, для которых вероятности Согласно основной теореме игр [38], каждая конечная игра имеет, по крайней мере, одно решение, которым может быть и смешанная стратегия. При использовании смешанной стратегии выигрыш игрока А – случайная величина с математическим ожиданием:
или в векторной записи
Для оптимальных стратегий имеет место соотношение:
Применение игроком А стратегии оптимальной стратегии Р* должно обеспечить ему при любых действиях игрока В математическое ожидание выигрыша не меньше цены игры n. Поэтому выполняются соотношения:
Аналогично для игрока В оптимальная стратегия
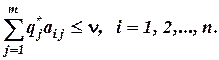
Соотношения (1.44) и (1.45) могут быть использованы при построении формальных математических моделей для определения решения игры. Рассмотрим, как выглядит модель выбора для определения стратегии при использовании соотношения (1.44). Введём новые переменные
а из условия
Так как решение игры должно максимизировать значение n, то для выбора оптимальной смешанной стратегии игрока А необходимо найти:
при
Аналогично может быть сформулирована задача для выбора оптимальной смешанной стратегии игрока В с использованием (1.45): найти при
Как видно из соотношения (1.48) и (1.49) для решения игры имеем пару двойственных задач линейного программирования. Используя свойство симметричности, можно решить одну из них, требующую меньших вычислений, а решение второй задачи найти, используя результаты теории двойственности (см. главу 2).
Пример 1.7 [34]
Рассматривается игра в хоккей. В одном из периодов состояния команд А и Б характеризуется следующим образом:
у команды А – 4 играющих пятёрки, у команды Б – 3 играющих пятёрки.
Матрица игрового преимущества имеет вид:
Задача (1.48) представлена в виде следующей модели:
при
Оптимальное решение задачи методом линейного программирования (см. главу 2) выглядит следующим образом:
Таким образом, цена игры равна
Поэтому в данном игровом периоде тренеру команды А необходимо реже выпускать первую пятёрку, а четвёртую вообще не включать в игру. Аналогично может быть сформулирована оптимальная стратегия и для команды Б.
Содержание предыдущих разделов убеждает в том, что среди математических методов, используемых в теории принятия решений, особую роль играют методы решения оптимизационных задач. Они составляют фундамент системы математического обеспечения проблем принятия решений. Этим вопросам будет посвящено содержание следующего раздела. Примеры построения операционных моделей Пример 1.8. Линейные модели Транспортная задача Предположим, что однородный продукт должен быть перевезен из т пунктов производства в п пунктов потребления, причем из каждого пункта производства вывозится установленное количество и в каждый пункт потребления ввозится также установленное количество продукта, так что общие спрос и предложение равны. Пусть из i -го пункта производства (i =1, 2,..., m) вывозится ai продукта, а в j -й пункт потребления должно быть ввезено bj продукта, причем величины эти известны. Тогда:
где Пусть xi j – неизвестное количество продукта, которое должно быть перевезено из i -го пункта производства в j -й пункт потребления. Тогда:
где Пусть стоимость перевозки из i -го пункта производства в j -й пункт потребления равна
Задача поставщика
Владелец кафе знает, что в связи с наступлением праздников в течение одной следующей недели ему в j -й день (
На стирку обычно требуется три дня, т.е. грязная салфетка отправленная в стирку в j -й день, вернется из стирки и может быть использована в (j+3) -ийдень. Однако в прачечной существует ускоренное обслуживание по повышенному тарифу, при котором салфетки возвращаются из стирки через два дня. Не имея на руках или в прачечной готовых к употреблению салфеток, владелец будет вынужден покупать салфетки по 25 рублей за штуку. Стоимость стирки – 10 и 15 рублей соответственно при обычном обслуживании и при ускоренном обслуживании. Как должен вести дело владелец кафе, чтобы удовлетворить потребность кафе в салфетках и минимизировать издержки за неделю? Построим математическую модель. Пусть x i, ( Так как необходимо минимизировать общую сумму, требуемую для поддержания количества салфеток на должном уровне, не следует покупать салфеток больше, чем требуется в данный день, или отправлять салфетку в прачечную, если она не будет использована в дальнейшем.
В первый день, т.е. в понедельник, необходимо купить такое количество салфеток, какое требуется, т.е. x 1 = 5. В этот день можно выбирать: послать ли все или некоторые из пяти грязных салфеток в быструю, медленную прачечную или оставить их в ящике для грязных салфеток. То, что происходит с этими пятью салфетками можно представить уравнением:
y1 + z1 + u1 = 5. (1.54)
Общая стоимость всех операций первого дня:
25x1 +15y1 + 10z1 (1.55)
Выпишем остальные ограничения данной модели, помня о том, что в нашей системе выстиранные салфетки возвращаются через 2 или 3 дня в зависимости от того, какой прачечной мы воспользовались.
Во вторник необходимо купить некоторое количество салфеток, а именно x2 = 6. После того, как их используют, мы поступим с ними и u1 грязными салфетками согласно уравнению: y2 + z2 + u2 = 6 + u1. (1.56)
Оно выражает тот факт, что у нас скопилось u1 грязных салфеток, оставшихся с понедельника и еще 6, оставшихся со вторника. Можно их отправить в стирку (y2 + z2), либо оставить в ящике с грязными салфет-ками (u2). Стоимость всех операций во вторник:
25x2 + 15y2 + 10z2. (1.57)
В среду нам потребуется 7салфеток. Это первый день, когда выстиранные салфетки из быстрой стирки можно употребить в дело. Поэтому нужные 7 салфеток можно получить, купив их или взяв их из того количества салфеток, которые были сданы в стирку в понедельник. Имеем:
x3 + y1 = 7. (1.58) Так же, как и ранее y3 + z3 + u3 = 7 + u2, (1.59)
а стоимость операции в среду равна:
25x3 + 15y3 + 10 z 3. (1.60)
Необходимые в четверг 8 салфеток могут быть либо новыми, либо выбранными из числа тех, которые мы посылали в быструю прачечную во вторник или в медленную прачечную в понедельник. Это можно записать как: x4 + y2 + z1 = 8 (1.61) y4 + z 4 + u4 = 8 + u3, (1.62)
а стоимость операций в четверг составит:
25x4 + 15y4 + 10z4.
Предположим, что нас интересует только одна неделя и, следовательно, мы не будем отдавать салфетки в стирку, если они не вернутся назад к воскресенью. Для пятницы имеем: x5 + y3 + z2 = 7. (1.63) y5 + u5 = 7 + u4 (1.64) а стоимость равна: 25x5 + 15y5. (1.65) Для субботы: x6 + y4 + z3 = 9 (1.66)
u6 = 9 + u5, а стоимость равна 25 x6 .
Для воскресенья имеем: x7 + y5 + z4 = 10 (1.67) u7 = 10 + u6, а стоимость равна 25 x7.
Объединяя полученные выше уравнения, получаем математическую модель операции:
при условиях:
Пример 1.9. Нелинейные модели
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.168 (0.009 с.) |


 и
и  каждого из игроков удовлетворяет соотношению:
каждого из игроков удовлетворяет соотношению: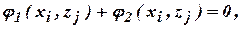 (1.39)
(1.39)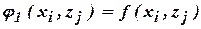 ,
,
 , в свою очередь, цель игрока В – минимизировать эту же функцию.
, в свою очередь, цель игрока В – минимизировать эту же функцию. Составим матрицу
Составим матрицу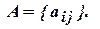 Матрица А называется платёжной, её строки соответствуют стратегиям
Матрица А называется платёжной, её строки соответствуют стратегиям  , столбцы – стратегиям
, столбцы – стратегиям  , элемент
, элемент  – выигрыш игрока А, если он выбрал стратегию
– выигрыш игрока А, если он выбрал стратегию  (1.40)
(1.40)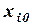 , обеспечивающая получение a, называется максиминной.
, обеспечивающая получение a, называется максиминной. . Естественно, что игрок В выберет такое значение j, при котором его максимальный проигрыш b минимизируется:
. Естественно, что игрок В выберет такое значение j, при котором его максимальный проигрыш b минимизируется: . (1.41)
. (1.41) минимаксной.
минимаксной.
 , (1.42)
, (1.42) .
.
 .
. 
 ,
, .
.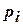 и
и  отличны от нуля, называются активными.
отличны от нуля, называются активными. ,
, . Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры n:
. Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры n: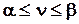 . (1.42)
. (1.42) . (1.43)
. (1.43) (1.44)
(1.44) должна обеспечить ему при любых действиях игрока А проигрыш, не превышающий цену игры n, т. е. справедливо соотношение:
должна обеспечить ему при любых действиях игрока А проигрыш, не превышающий цену игры n, т. е. справедливо соотношение: Тогда (1.44) перепишется следующим образом:
Тогда (1.44) перепишется следующим образом: (1.46)
(1.46) следует, что
следует, что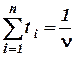 . (1.47)
. (1.47) (1.48)
(1.48)
 (1.49)
(1.49)


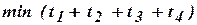


 , а оптимальные вероятности использования чистых стратегий в смешанной стратегии тренеров команды А определились следующим образом:
, а оптимальные вероятности использования чистых стратегий в смешанной стратегии тренеров команды А определились следующим образом:
 , (1.50)
, (1.50) для всех i ¹ j.
для всех i ¹ j. (1.51)
(1.51) , (1.52)
, (1.52) ³ 0 для всех i и j.
³ 0 для всех i и j. . Эти величины также заданы. Задача состоит в том, чтобы найти
. Эти величины также заданы. Задача состоит в том, чтобы найти  . (1.53)
. (1.53) ) потребуется rj чистых салфеток:
) потребуется rj чистых салфеток: ) количество новых салфеток, купленных в соответствующий день недели, Аналогично, пусть y i, z i, (
) количество новых салфеток, купленных в соответствующий день недели, Аналогично, пусть y i, z i, (





