
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение достоверности результатов проведённого опросаСодержание книги Поиск на нашем сайте
Базовой статистической характеристикой для определения степени согласованности мнений экспертов является коэффициент конкордации W [33]. В случае строгого ранжирования (отсутствуют критерии, находящиеся на одной позиции) значение W определяется следующим образом:
где r – число критериев, m – число экспертов,
В случае нестрогого ранжирования:
где
Значение W находится в пределах W = 0 означает полную противоположность, а W = 1 – полное совпадение ранжировок. Практически, достоверность экспертного опроса считается хорошей, если
Б. Метод непосредственной численной оценки В качестве степени согласованности служит дисперсия:
где (при отсутствии информации о компетентности экспертов можно считать
При решении многокритериальной задачи соответствующие оценки дисперсии (1.20) могут быть получены по каждому из критериев. Используя распределение Стьюдента [33], можно определить статистическую значимость результатов и построить соответствующие доверительные интервалы. Если выбранные критерии согласованности не выполнены, то необходимы повторные экспертизы либо с расширением числа участников, либо с представлением экспертам дополнительной информации. Кроме того, в этом случае должны быть приняты специальные организационные меры, чтобы обеспечить достаточную достоверность результатов. Соответствующие правила и процедуры, конечно, во многом зависят от содержания конкретных экспертиз, но тем не менее может быть высказан целый ряд общих соображений, которые достаточно хорошо сформулированы в методе «Дельфы» [31]. Данный метод широко использовался в США для решения разнообразных политических, экономических, социальных и военных проблем. Метод получил название по имени древнегреческого города Дельфы, где по преданию находился известный дельфийский оракул.
Метод Дельфы содержит серию рекомендаций.
1. Экспертами могут быть только признанные специалисты в соответствующей области.
2. Так как каждый эксперт может ошибаться, то только мнение достаточно большого числа экспертов может удовлетворительно охарактеризовать исследуемый вопрос.
3. Вопросы, которые ставятся экспертам, должны быть относительно просты и поставлены настолько чётко, чтобы исключить неоднозначность толкования.
4. Исключаются открытые дискуссии, но допускается процедура получения и анализа экспертами дополнительной информации.
5. Лица, организующие экспертизы, должны проявлять большой такт, чтобы в максимальной степени исключить влияние организаторов опроса на мнение экспертов. Построение результирующей оценки
Пусть в результате выбранной процедуры опроса построена матрица
где r – число критериев, m – число экспертов, Процедура построения результирующей оценки зависит от процедуры проведения опроса.
Ранжирование
Для построения средней оценки вводится в соответствии с [33] понятие расстояния между ранжировками
При наличии m ранжировок Медиана Кемени
где m – число экспертов,
Наряду с принципом Кемени, для выбора результирующего ранжирования часто используется принцип большинства. Он состоит в следующем: на первое место в результирующую ранжировку попадает критерий, который большинство экспертов поставили на первое место, на второе – критерий, который поставили на второе и т. д. Однако, как показано в [33], данный принцип в отличие от принципа Кемени не всегда приводит к выбору наилучшего решения.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.006 с.) |

 (1.18)
(1.18) – ранг, выставленный j – м экспертом i – му критерию.
– ранг, выставленный j – м экспертом i – му критерию. (1.19)
(1.19) – число групп равных рангов, введённых j - м экспертом;
– число групп равных рангов, введённых j - м экспертом; – количество дробных рангов в l - ой группе, введённых j - м экспертом.
– количество дробных рангов в l - ой группе, введённых j - м экспертом. , причём, случай
, причём, случай
 .
. (1.20)
(1.20)
 – веса экспертов,
– веса экспертов, ),
),  – оценка j -го эксперта.
– оценка j -го эксперта.
 – мнение j – го эксперта об относительной ценности i –го критерия.
– мнение j – го эксперта об относительной ценности i –го критерия. проведёнными k –ым и l –ым экспертами:
проведёнными k –ым и l –ым экспертами: . (1.21)
. (1.21)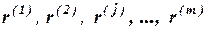 , проведённых m экспертами, результирующей считается та сумма расстояний от которой до исходных есть величина наименьшая из всех возможных. Такая ранжировка называется медианой Кемени.
, проведённых m экспертами, результирующей считается та сумма расстояний от которой до исходных есть величина наименьшая из всех возможных. Такая ранжировка называется медианой Кемени. находится из задачи минимизации по всем возможным ранжировкам из множества R (таких ранжировок r!) суммы расстояний от r до
находится из задачи минимизации по всем возможным ранжировкам из множества R (таких ранжировок r!) суммы расстояний от r до  , т.е. определяется формулой:
, т.е. определяется формулой: , (1.22)
, (1.22)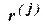 – ранжировка на множестве критериев, проведённая j -м экспертом.
– ранжировка на множестве критериев, проведённая j -м экспертом.


