
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений в условиях неопределённостиСодержание книги Поиск на нашем сайте
Задача принятия решений в условиях неопределённости фактически называется «игрой с природой». Природа выступает в роли внешней среды. ЛПР должен сделать некоторый выбор из множества допустимых альтернатив, принятие которых зависит от того, какое конкретное состояние природы будет наблюдаться. При этом предполагается, что множество состояний природы не известно ЛПР. Множество неопределённых факторов можно разделить на объективныеи субъективные.
Субъективная неопределённость характеризует индивидуальные психофизические параметры ЛПР. Основные причины её возникновения:
· неполнота знаний ЛПР о закономерностях и условиях развития ситуации или самой системы,
· неверная мотивация при выборе альтернатив,
· отсутствие информации о наличии в рассматриваемом процессе или системе активных элементов, обладающих возможностями и правами по выбору управления и др.
Причинами возникновения объективной неопределённости служат:
· неполнота информации об операции,
· неопределённость цели функционирования,
· наличие случайных факторов,
· неопределённость процедуры принятия решений из-за громоздкости многоуровневой системы управления операцией, либо наличие возможности образования коалиций с противоположными интересами в структуре управления.
В дальнейшем обозначим любую неопределённость векторным параметром
К наиболее часто используемым методам выбора оптимальной стратегии в условиях неопределённости можно отнести [37]:
1) принцип максимума (критерий Вальда),
2) принцип оптимизма,
3) принцип Гурвица,
4) принцип Сэвиджа,
5) принцип Лапласа.
Для иллюстрации указанных выше принципов, считаем, что Х дискретно, т. е. Критерии выбора оптимальной стратегии в соответствии с указанными выше принципами имеют следующий вид:
1. Критерий Вальда (гарантированного результата):
2. Критерий оптимизма:
3. Критерий Гурвица (комбинированный критерий):
4. Критерий Сэвиджа:
где 5. Критерий Лапласа:
Рассмотрим применение указанных критериев в условиях неопределённости на простом примере. Пример 1.4
Задана таблица исходных данных (табл.1.5).
Таблица 1.5
Оптимальные решения:
для критерия Вальда – решение для критерия оптимизма – решение для критерия Гурвица – решение
для критерия Сэвиджа – решение
для критерия Лапласа – решение
Пример 1.5 [34]
Тренерский коллектив лыжной команды обсуждает вариант мази для лыж. Тренеры знают, что во время лыжной гонки погода (природа) может находиться в трёх состояниях
Элемент
Тренер-пессимист руководствовался критерием Вальда. Критерий ориентирован на худшие погодные условия и носит явно пессимистиче-ский характер. Стратегия, предложенная пессимистом была
Тренер-оптимист как всегда ориентировался на лучшее и предло-жил четвёртый вариант смазки
Старший тренер-рационалист, выслушав свою команду, предложил использовать критерий пессимизма-оптимизма Гурвица при
Представитель тренерского совета (возмутитель спокойствия) предложил:
1) исключить стратегию
2) вместо матрицы успехов А ориентироваться на матрицу рисков
В соответствии с этим следует выбирать такую стратегию, при которой величина риска окажется наименьшей в самой неблагополучной ситуации, т.е. необходимо выбрать стратегию
Старший тренер, подводя итог дискуссии, заметил, что последнее предложение немногим лучше предложения «пессимиста»; различие лишь в том, что по предложенному критерию наихудшим следует считать не минимальный выигрыш, а максимальный риск. Это хорошо известный критерий Сэвиджа. Критерий этот столь же пессимистичен, как и «максиминный» критерий Вальда. Поэтому, придерживаясь золотой середины, целесообразно остановиться на стратегии Выбор критерия из рассмотренных является наиболее сложным и ответственным этапом в исследовании операций. При этом не существует каких-либо общих рекомендаций и советов. Выбор критерия должен быть в максимальной степени согласован с конкретной спецификой задачи, а также с поставленными целями. Например, если минимальный риск недопустим, то следует применять критерий Вальда.
1.6.2. Принятие решений в условиях риска
В отличие от условий полной неопределённости на множестве Z задана вероятностная метрика. Если множество Z дискретно, то каждому
В этих условиях наиболее распространённым принципом принятия решений является принцип Байеса:
При равновероятном распределении:
решения, выбранные в соответствии с принципом Байеса (1.35) и Лапласа (1.34) совпадают. Если множество Z непрерывно, то на множестве задаётся диффе-ренциальный или интегральный закон распределения вектора z Î Z. В этом случае возможны различные постановки задач выбора оптимального решения:
где Рассмотренные задачи, строго говоря, не эквивалентны. Выбор любой из них отражает предположение о том, что определение решения в соответствие с выбранной постановкой обеспечивает требуемую эффективность операции. Постановка (1.36) соответствует использованию принципа Байеса в непрерывном случае.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.006 с.) |

 , где Z – множество неопределённостей, а вектор z учитывает любые неконтролируемые, неуправляемые для ЛПР факторы операции. Эффективность операции определяется скалярным критерием
, где Z – множество неопределённостей, а вектор z учитывает любые неконтролируемые, неуправляемые для ЛПР факторы операции. Эффективность операции определяется скалярным критерием  , где
, где  , причём необходимо найти
, причём необходимо найти  .
.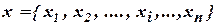 , Z также дискретно, т. е.
, Z также дискретно, т. е.  , а исходная информация для принятия решения представлена таблицей
, а исходная информация для принятия решения представлена таблицей  .
.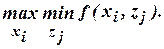 (1.29)
(1.29) (1.30)
(1.30)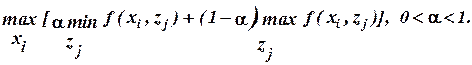 (1.31)
(1.31) (1.32)
(1.32) . (1.33)
. (1.33) (1.34)
(1.34)







 .
. . В их распоряжении имеется четыре типа лыжной мази
. В их распоряжении имеется четыре типа лыжной мази  . Матрица А вероятностей удачного прохождения трассы гонки спортсменами известна:
. Матрица А вероятностей удачного прохождения трассы гонки спортсменами известна:
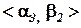 означает, что если будет использоваться мазь
означает, что если будет использоваться мазь  , и природа будет находиться в состоянии, то с вероятностью 0.8 эта мазь позволит спортсмену пройти дистанцию в полную силу. Вероятности состояний погоды тренерам были неизвестны (недоверие прогнозам погоды) и поэтому на тренерском совете им пришлось решать вопрос о том, какою мазью следует мазать лыжи.
, и природа будет находиться в состоянии, то с вероятностью 0.8 эта мазь позволит спортсмену пройти дистанцию в полную силу. Вероятности состояний погоды тренерам были неизвестны (недоверие прогнозам погоды) и поэтому на тренерском совете им пришлось решать вопрос о том, какою мазью следует мазать лыжи. , так как выигрыш, соответствующий благоприятной погоде, наибольший.
, так как выигрыш, соответствующий благоприятной погоде, наибольший. и в соответствии этим выбрать стратегию
и в соответствии этим выбрать стратегию  из рассмотрения, так как она заведомо хуже стратегии
из рассмотрения, так как она заведомо хуже стратегии  , где
, где  – отклонение выигрыша
– отклонение выигрыша 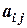 от максимально возможного, получаемого при условии заблаговременной информации о том, что природа находится в состоянии
от максимально возможного, получаемого при условии заблаговременной информации о том, что природа находится в состоянии  . Матрица рисков
. Матрица рисков  выглядит следующим образом:
выглядит следующим образом: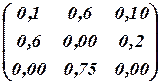 .
. или
или  соответствует вероятность
соответствует вероятность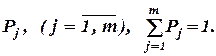
 . (1.35)
. (1.35)
 (1.36)
(1.36) (1.37)
(1.37) (1.38)
(1.38)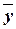 – математическое ожидание вектора y.
– математическое ожидание вектора y.


