
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о загрузке судна запасными деталямиСодержание книги Поиск на нашем сайте
Пусть рассматривается три типа запасных деталей, имеющих объемы 1, 2, и 2 единицы. Общий объем склада равен 10 единицам. Штрафные затраты pj, возникающие при неудовлетворении потребности, равны соответствен-но 800, 600, и 1300. Будем предполагать, что спрос n j на каждую из запасных деталей подчинен пуассоновскому распределению со средними значениями m j = (4; 2; 1). Соответственно требуется определить, каким должен быть запас деталей каждого типа, чтобы средние штрафные издержки были минимальными. В математической формулировке мы приходим к следующей модели: найти
при условиях: xj ³ 0, целые, j = 1, 2, 3; x1 + 2x2 + 2x3 £ 10, где xj – запасы деталей j -го типа. Выражение
в функции (1.75) представляет собой вероятность случайной величины nj, подчиненной закону Пуассона, а m j есть ожидаемая средняя потребность в деталях j -го типа: Из (1.76) следует, что
Таким образом, можно записать:
где
Соотношение (1.78) дает возможность без труда вычислить средний спрос на j -ю деталь, возникающий в то время, когда запас их исчерпан, пользуясь таблицами для распределения Пуассона. Задачи
1. Диспетчерская служба имеет следующие минимальные потребности в количестве диспетчеров в различное время суток (табл. 1.6):
Таблица 1.6
При этом нужно иметь в виду, что период 1 следует сразу же за периодом 6. Каждый диспетчер ежедневно приступает к работе в начале определенного периода и работает восемь часов без перерыва. Требуется составить расписание на каждые сутки таким образом, чтобы обойтись минимальным числом диспетчеров, не нарушая, при этом, сформулированных выше требований.
2. В обработку поступили две партии досок для изготовления комплектов из трех деталей, причем первая партия содержит 50 досок длиной по 6,5 м, вторая содержит 200 досок длиной 4 м. Каждый комплект состоит из двух деталей по 2 м каждая и одной детали по 1,25 м. Как распилить доски, чтобы получить наибольшее число комплектов?
3. На заводе предстоит решить, какое количество х1 чистой стали и какое количество х2 металлолома следует использовать для приготовления (из соответствующего сплава) литья для одного из своих заказчиков. Пусть производственные затраты на 1 т стали составляют 3 усл. ед., а затраты на 1 т металлолома 5 усл. ед. (последняя цифра больше предыдущей, т.к. использование металлолома связано с его предварительной очисткой). Заказ предусматривает поставку не менее 5 т литья. Предположим, что предназначенные для литья запасы чистой стали составляют 4 т, а металлолома – 6 т. Отношение веса металлолома к весу чистой стали в сплаве не должно превышать 7/8. Производственно-технологические условия таковы, что на процессы плавки и литья может быть отведено не более 18 час., при этом на 1 т стали затрачивается от 2,5 до 3 час., а на 1т металлолома от 1,5 до 2 час. Цель завода – выполнить заказ с минимальными производственными затратами. 4. Предприятие выпускает радиоприемники трех различных моделей: модель А, модель В и модель С. Каждое изделие указанных моделей приносит доход в размере 8, 15, 25 единиц стоимости соответственно. Необходимо, чтобы фирма выпускала не менее 100 приемников модели А, 150 приемников модели В и 75 приемников модели С. Каждая модель характеризуется определенным временем, необходимым для изготовления соответствующих деталей, сборки изделия и его упаковки. Так, в частности, в расчете на 10 приемников модели А требуется 3 ч. для изготовления соответствующих деталей, 4 ч. на сборку и 1 ч. на упаковку. Соответствующие показатели на 10 приемников модели В равняются 3; 5, 5 и 1,5 ч., а на 10 приемников модели С – 5, 8 и 3. В течение ближайшей недели фирма может израсходовать на производство – 150 ч., на сборку – 200 ч. и на упаковку – 60 ч. Составить производственный план. 5. На предприятии требуется произвести раскрой рулона материала шириной 60 см. Мастер сообщил следующие данные о заказах текущей недели:
Предполагается, что количество рулонов с шириной 60 см достаточно для того, чтобы удовлетворить все недельные заказы. Найти план раскроя, минимизирующий общие суммарные потери.
6. В небольшом населенном пункте А имеется школа, которую посещает некоторое число учеников, при этом место жительства 72 учеников находится вне населенного пункта, что приводит к необходимости организовать их доставку к школе на автобусах. Имеются две основные автобусные остановки В, С (В находится между А и С). Число учеников, нуждающихся в доставке к школе на автобусе равняется 42 на остановке С, 6 – между С и В, 20 на остановке В и 4 – между В и А (рис.1.4).
Рис. 1.4
Транспортное агентство, обслуживающее пункт А, располагает двумя типами автобусов: автобусы на 35 и 50 мест. Транспортным агентством установлены следующие цены проездных билетов для каждого из отрезков пути в зависимости от типа автобуса:
Необходимо определить, какого типа автобусы следует использовать на каждом участке пути так, чтобы суммарные издержки школьников были минимальными.
7. Определить максимальный поток f из пункта О в пункт М при ограниченной пропускной способности путей. Граф путей представлен на рис 1.5.
Числа над дугами графа определяют верхнюю границу потока на соответствующих путях.
8. Информация о проекте задана перечнем работ, их продолжительностью и последовательностью выполнения (табл. 1.7):
Таблица 1.7
В i - ю работу можно вложить средства, где xi £ ci, при этом время выполнения работы уменьшится до t i(1 - bi xi).
Пусть: b1 = 0.2, c1 = 2, b4 = 0.3, c4 = 2, b8 = 0.1, c8 = 5. Определить размер вложенных средств x1 , x4 , x8 в 1-ю, 4-ю, 8-ю работы так, чтобы время завершения всего комплекса работ не превышало 40 месяцев. Сформулировать общую задачу минимизации суммы вложений, необходимых для того, чтобы обеспечить завершение всего комплекса работ к заданному моменту времени Т, как задачу линейного программирования.
9. Участник экспедиции укладывает рюкзак, и ему требуется решить, какие положить продукты. В его распоряжении имеются мясо, мука, сухое молоко и сахар. В рюкзаке для продуктов осталось лишь 45 дм3 объема, и нужно, чтобы суммарная масса продуктов не превосходила 35 кг. Врач экспедиции рекомендовал, чтобы мяса (по массе) было больше муки по крайней мере в два раза, муки не меньше молока, а молока по крайней мере в восемь раз больше, чем сахара. Сколько и каких продуктов нужно положить в рюкзак, с тем, чтобы суммарная калорийность продуктов была наибольшей? Характеристики продуктов приведены в табл. 1.8.
Таблица 1.8
10. Организация хранит различную информацию, записанную на магнитных носителях. Организации необходимо составить статистические данные по различным демографическим характеристикам (например, как распределение населения по возрастным группам, распределение доходов, обеспеченность жильем и т.п. по выбранным восьми городским районам. Предположим, что вся требуемая информация хранится в n массивах. Примем, что t j (j = 1, 2,..., n) – время поиска ЭВМ нужной информации в массиве j и что время поиска не зависит от числа характеристик, выбираемых из массива. Некоторые из m видов данных записаны более чем в одном из n массивов, т.е. различные массивы содержат информацию, относящуюся к одной и той же характеристике. Расположение информации задано матрицей
а) Построить модель для определения того, в каких из n массивов производить поиск, чтобы выбрать данные, относящиеся ко всем требуемым статистическим характеристикам за минимальное время.
б) Объясните, как следует изменить модель, если время поиска в массиве j равно
11. Для производства комплексной продукции требуется изготовить два вида изделий. Их изготовление может быть поставлено на каждом из пяти типов предприятий. Производственная мощность предприятия и количество предприятий каждого типа даны в табл. 1.9.
Таблица 1.9
Определить, сколько предприятий каждого типа надо поставить на производство первого и сколько на производство второго изделия, чтобы обеспечить максимальный выпуск комплектов, если в каждый комплект должно входить два изделия первого вида и одного второго.
12. На мебельной фабрике требуется раскроить 5000 прямоугольных листов фанеры размером 4 х 5 м каждый с тем, чтобы получить два вида прямоугольных деталей: деталь А должна иметь размер 2 х 2 м, деталь Б – размер 1х 3 м. Необходимо, чтобы деталей А оказалось не меньше, чем деталей Б. Каким образом следует произвести раскрой, чтобы получить минимальное (по площади) количество отходов? 13. Построить математическую модель для выбора расписания при следующих условиях:
- задан состав операций: а1 , а2 ,..., а10 ; - заданы временные функции: t1, t2 ,..., t10 ; - заданы ограничения на порядок следования: а1 - некоторые операции нельзя выполнять - одновременно: (а1 и а2), (а5 и а7); - целевая функция – минимизация общей длительности.
14. (241). Для строительства домов на 100 строительных площадках выбраны 5 типовых проектов. По каждому из проектов известны длительность закладки фундаментов, возведения стен и крыш, отделка, а также жилая площадь дома. Возможно, исходя из трудовых, сырьевых и технических ресурсов одновременное ведение закладки 10 фундаментов и строительства и отделки 15 зданий (см. табл. 1.10).
Таблица 1.10
Составить план строительства, максимизирующий ввод жилой площади в течение года (300 рабочих дней) при условии, что домов II типа должно быть построено не меньше 10.
15. Автозавод выпускает две модели автомобилей: модель А и более дешевую модель В. На заводе работает 1000 неквалифицированных и 800 квалифицированных рабочих, каждому из которых оплачивается 40 часов в неделю. Для выпуска модели А требуется 30 ч. неквалифицированного и 50 ч. квалифицированного труда. Для модели В – 40 ч. и 20 ч. cоответ-ственно. Каждая из моделей требует затрат на сырье в размере 500 руб. и 1500 руб. Суммарные затраты не должны превышать 900 000 руб. в неделю. Рабочие, осуществляюшие доставку, работают по 5 дней в неделю и могут забрать с завода не более 210 машин в день. Каждая модель А (В) приносит прибыль 1000 (500) руб. Каким должен быть объем выпуска каждой модели?
16. Фирма производит 2 модели А и В сборных книжных полок. Их производство ограничено наличием сырья (досок) и временем машинной обработки. Для каждого изделия А требуется 3 м2 досок, для В – 4 м2. Фабрика может получить от поставщиков 1700 м2 досок в неделю. Для каждого изделия А (В) требуется 12 (30) мин. машинного времени. В неделю можно использовать не более 160 ч. машинного времени. Определить план недельного выпуска, максимизирующий прибыль, если изделие А (В) приносит денежную прибыль 2 (4) усл. един.
17. В некоторой местности в пунктах А и В имеются потребности в дополнительном транспорте. В пункте А требуется 5 дополнительных автобусов, в пункте В – 7. Известно, что 3, 4, 5 автобусов соответственно могут быть получены из гаражей G1 , G2 , G3 . Как следует распределить эти автобусы между пунктами А и В, чтобы минимизировать их суммарный пробег. Расстояния между гаражами и пунктами А и В заданы табл. 1.11.
Таблица 1.11
18. Фирма производит два продукта А и В, продаваемых соответственно по 8 и по 15 руб. за упаковку. Рынок сбыта для каждого из них не ограничен. Продукт А обрабатывается на машине 1, продукт В – на машине 2, затем оба упаковываются на фабрике. 1 кг сырья стоит 6 копеек. Машина 1 (2) обрабатывает 5000 (4000) кг сырья в час с потерями 10 % (20 %). Машина 1 (2) работает 6 (5) часов в день, ее использование стоит 288 (336) руб./час. Упаковка продукта А (В) весит 1/4 (1/3) кг. Фабрика может работать 10 час. в день, производя в 1 час продукцию стоимостью 360 руб. За 1 час можно упаковать 12 000 продуктов А и 8 000 продуктов В. Компания хочет определить такие значения х1 и х2 потребления сырья для продуктов А и В (в тыс. кг), при которых дневная прибыль максимальна.
19. Для обеспечения автоперевозок в j -й день недели требуется aj автомашин. Машины после поездки должны пройти профилактический ремонт. Обычный ремонт длится 4 дня при затратах 20 руб. на машину, срочный ремонт длится 2 дня при затратах 30 руб. на машину. Кроме того, можно использовать машины для перевозок, сняв их с другого участка, что приводит к потерям 50 руб. на машину. Определить оптимальную недельную программу подготовки машин, минимизирующую суммарные затраты автобазы, если потребность в машинах характеризуется следующими данными (табл. 1.12). Для решения использовать пример задачи о поставщике. Таблица 1.12
Задачи из Калихмана Калихман И.Л. Сборник задач по математическому программированию. изд. 2-е, доп. и перераб. М. «Высшая школа», 1975, 270 с.
20 (194). Производственная мощность завода позволяет производить за месяц 200 электродвигателей типа А или 600 электродвигателей типа В. Определить, сколько электродвигателей каждого ипа должен производить завод для достижения максимума товарной продукции при следующих условиях: 1. двигатели обоих типов имеют одинаковую цену 2. цена на двигатель типа А в 3 раза больше цены на двигатель типа В 3. цены на двигатели типов А и В относятся как 9:2.
21 (195). Механический цех может изготовить за смену 600 деталей №1 или 1200 деталей №2. Производственная мощность термического цеха, куда эти детали поступают на термообработку в тот же день, позволяет обработать за смену 1200 деталей №1 или 800 деталей №2. Цены на детали одинаковые. Определить ежедневную производственную программу выпуска деталей, максимизирующую товарную продукцию предприятия, при следующих условиях: 1. оба цеха работают в одну смену 2. механический цех работает три смены, а термический – две смены; 3. предприятие работает в две смены, при этом деталей № 1 должно быть изготовлено не более 800 шт. и деталей №2 не более 1000 шт.
22 (196). Автомобильный завод машины типов А и В. Производственные мощности отдельных цехов или отделов приведены в следующей таблице:
Определить наиболее рентабельную производственную программу при следующих дополнительных условиях: 1. прибыли от выпуска одной машины типов А и В соответственно равны 2000 и 2400 руб. 2. выпуск одной машины А приносит прибыль, в два раза меньшую, чем выпуск одной машины типа В. 3. Производственная мощность 1-го и 5-го цехов может быть увеличена в 1,5 раза за счет сверхурочных работ, уменьшающих прибыль от выпуска одной машины типа А до 1500 руб., одной машины типа В – до 2100 руб.
23 (197). Из пункта А в пункт В ежедневно отправляются пассажирские и скорые поезда. В таблице указан наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные поезда, и количество пассажиров, вмещающихся в каждом из вагонов:
Определить оптимальное число скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума.
24 (199). Оборудование фабрики позволяет выпускать фруктовые компоты в трех видах тары: стеклянной вместимостью 10 л., жестяной вместимостью 8 л., полиэтиленовой вместимостью 5 л. Найти производственную программу предприятия, если себестоимость 1 л. компота составляет: в стеклянной таре 16 руб, в жестяной – 10 руб и в полиэтиленовой таре – 16 руб. Отпускная цена независимо от тары составляет 40 руб за литр.
25 (216). Произвести распил 5-метровых бревен на брусья размерами 1,5; 2,4 и 3,2 м в отношении 2: 3: 5 так, чтобы минимизировать общую величину отходов.
26 (206). Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготовления ткани используются пряжа и красители. В следующей таблице указаны мощности станков (в тыс. станко-часов), ресурсы пряжи и красителей (в тыс. кг), производительности станков по каждому виду пряжи (в м/час). нормы расхода пряжи и краски (в кг на 1000 м) и цена (в руб) 1 м ткани.
По эти исходным данным решить следующие задачи. 1. Определить оптимальный план выпуска тканей, максимизирующий товарную продукцию (выручку) фабрики. 2. Решить задачу 1, приняв дополнительное условие, что количество тканей трех артикулов должно находиться в отношении 2: 1: 3.
27 (214). На распил поступают 93 бревна длиной 3 м. Изготавливаются комплекты бревен. В каждый комплект бревен входят 2 бревна длиной 0,6 м, 1 бревно длиной 1,5 м и 3 бревна длиной 2,5 м. Определить план распила, обеспечивающий максимальное число комплектов.
28. На распил поступают 93 бревна длиной 3 м и 56 бревен длиной 5,5 м. Изготавливаются 2 комплекта бревен. В первый входят 2 бревна по 1,25 м и 1 бревно длиной 3,5 м. Во второй комплект — 3 бревна длиной 2,5 м, 1 бревно длиной 1,25 м и 2 бревна длиной 3,5 м. Количество комплектов первого типа должно быть не меньше количества комплектов второго типа. Определить план распила, обеспечивающий минимальное количество отходов.
29. Решить задачу 23 при условии, что пропускная способность дороги не позволяет в день пройти более, чем шести пассажирским поездам.
30 (220). Предприятие может выпускать продукцию по трем технологически отработанным способам производства. При этом за 1 час по 1-му способу производства оно выпускает 20 ед продукции, по 2-му — 25 ед и по 3-му — 30 ед продукции. Количество ресурсов, расходуемых за час при различных способах производства, и предельные запасы этих ресурсов представлены в следующей таблице.
Спланировать работу предприятия из условия получения максимума продукции, если известно, что общее время работы предприятия составляет 30 часов. 31 (221). Предприятие может работать по пяти технологическим процессам, причем количество единиц выпускаемой продукции по разным технологическим процессам за 1 ед времени соответственно равно 300, 260, 320, 400 и 450 шт. В процессе производства учитываются следующие производственные факторы: сырье, электроэнергия, зарплата и накладные расходы. Затраты соответствующих факторов в рублях при работе по разным технологическим процессам в течение 1 ед времени указаны в следующей таблице.
В последнем столбце таблиц указаны ресурсы, которыми располагает предприятие по каждому из производственных факторов. Найти программу максимального выпуска продукции.
32 (205). Мебельная фабрика выпускает столы, стулья, бюро и книжные шкафы. При изготовлении используются два типа досок, причем фабрика имеет в наличии 1500 м досок 1-го типа и 1000 м досок 2-го типа. Кроме того, заданы трудовые ресурсы в количестве 800 чел-час. В таблице приводятся нормативы затрат каждого из видов ресурсов на изготовление 1 ед изделия и прибыль от реализации 1 ед изделия.
По этим исходным данным решить следующие задачи. 1. Определить оптимальный ассортимент, максимизирующий прибыль 2. Решить ту же задачу при дополнительных условиях, налагаемых на ассортимент: столов — не менее 40, стульев — не менее 130, бюро — не менее 30 и книжных шкафов — не более 10. 3. Решить задачу 1 при условии комплектности: количество столов относится к количеству стульев, как 1: 6. 4. Заданы дополнительно цены: стол — 32 руб, стул — 15 руб, бюро — 12 руб и книжный шкаф — 80 руб. Определить оптимальный ассортимент, максимизирующий выручку при ограничении на ассортимент: количество столов относится к количеству стульев, как 1: 6. 5. Фабрика может дополнительно приобрести доски 1-го типапо 12 коп/м и 2-го типа по 8 коп/м. Кроме того, можно увеличить трудовые ресурсы за счет сверхурочной работы, производя дополнительную оплату каждого часа в сумме 80 коп. Определить в условиях задачи 1, увеличение какого из видов ресурсов более целесообразно
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.208.236 (0.01 с.) |

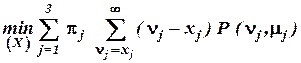 (1.75)
(1.75)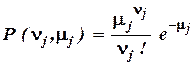 (1.76)
(1.76) .
.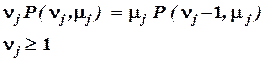 . (1.77)
. (1.77)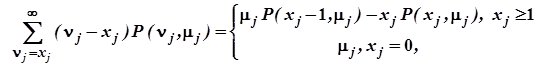 , (1.78)
, (1.78)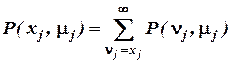 .
.
 А (4) В (20) (6) С (42)
А (4) В (20) (6) С (42)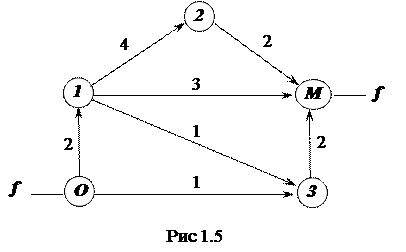
 , где
, где 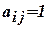 , если данные по i -ой характеристике записаны в j -ом массиве и
, если данные по i -ой характеристике записаны в j -ом массиве и  в противном случае.
в противном случае.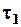


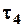
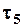
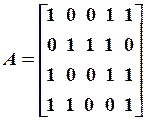 ,
,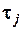 плюс t i j в случае, когда в результате поиска получают характеристику с индексом i. Соответствующие данные по значениям t i j приводятся в матрице
плюс t i j в случае, когда в результате поиска получают характеристику с индексом i. Соответствующие данные по значениям t i j приводятся в матрице  .
.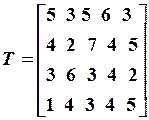
 а2 , а8
а2 , а8 


