
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы формирования свёртки критериевСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В случае использования аддитивных преобразований свёртка выглядит следующим образом:
где b i (x) – коэффициент важности соответствующего критерия Аддитивное преобразование для построения единого критерия очень часто используется, если объединение различных частных критериев проводится на экономической основе. В случае использования мультипликативной свёртки обобщённый критерий формируется следующим образом:
где Использование преобразования (1.5) характерно для тех задач принятия решений, где частными критериями являются некоторые вероятностные характеристики или где возможно использование в качестве Например, обобщённый критерий технико-экономической эффективности ЭВМ, предложенный в [36], построен следующим образом:
где
Т – время живучести ЭВМ.
Если критерии
где
К недостаткам данного метода можно отнести существование возможных неоднозначных компенсаций значений критериев. Введение метрики в пространстве целевых функций
Предположим, что решена система однокритериальных задач:
Совокупность скалярных величин Введём метрику в виде эвклидова расстояния от точки
в пространстве критериев:
В качестве нового скалярного критерия можно принять функцию (1.9). Её минимизация даёт исследователю определённую полезную информацию и показывает предельные возможности достижения абсолютного максимума.
Метод максиминной свёртки Задаётся некоторая система нормативов:
В таких случаях интегральный критерий удобно представить в виде:
и искать вектор х *, который обеспечивает максимальное значение F(x). Если значения
Метод последовательных уступок
Все критерии Процедура построения компромиссного решения сводится к следующему. Сначала ищется решение, обращающее в максимум главный критерий Далее снова назначается уступка в критерии Такой способ компромиссного решения хорош тем, что здесь сразу видно, ценой какой уступки в одном критерии приобретается выигрыш в другом. Компромиссы Парето
Все рассмотренные выше способы разрешения многокритериальной проблемы выбора были основаны на различных операциях свёртывания скалярных критериев к интегральным. К решению многокритериальных задач можно подойти с других позиций – попытаться сократить множество исходных вариантов, т. е. исключить из неформального анализа те варианты решений, которые заведомо плохи. Один из подобных путей был предложен итальянским экономистом Парето в 1904 г. Для раскрытия содержания этого подхода воспользуемся теоретико-множественной интерпретацией, для чего введём следующие операции и понятия [33].
Содержательный смысл этого определения состоит в том, что задание подмножества R на множестве W x W определяет, какие пары находятся в отношении R. Это подчёркивается следующим соглашением об обозначениях: если пара
Множество W называется областью задания отношения и в тех случаях, где существенна область задания отношения, используется пара обозначений Пример 1.1
Пусть W 1 – множество студентов группы, W 2 – множество студентов факультета, W 3 – множество студентов всего института. Естественно определяются три разных отношения: Способы задания отношений
Существуют три основных способа задания отношений: · матрицей, · графом, · сечениями.
Матричный способ. Общее правило задания матрицы отношения формулируется так:
где
Задание графом Элементы конечного множества W – вершины графа. От элемента Задание сечениями. Этот способ менее распространён, чем предыдущие, однако он пригоден и для задания отношений на бесконечных множествах.
Таким образом, множество Множество
На рис 1.1 изображены верхнее и нижнее сечения отношения Р в точке
Из определения множества следует, что Пример 1.2 Пусть
Множества  и и  изображены на рис. 1.2. изображены на рис. 1.2.
Легко видеть, что
Таким образом, множество Парето Переходя к многокритериальному пространству где хТ = [ х1, х2,..., х j,.,. хn ], отношение Парето в соответствии с определением 4 представляет собой следующее отношение доминирования:
Множество, включающее в себя все эффективные элементы х множества Отображение множества
Заметим, что принцип Парето не выделяет единственного решения, он только сужает множество альтернатив, окончательный выбор остаётся за ЛПР на основе дополнительной информации о его предпочтениях.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.251.240 (0.012 с.) |

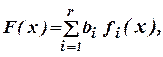 (1.4)
(1.4)
 (1.5)
(1.5) – некоторые вещественные числа.
– некоторые вещественные числа.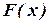 некоторых удельных характеристик.
некоторых удельных характеристик. (1.6)
(1.6) и отражает эффективное быстродействие ЭВМ, причём является критерием оценки технической эффективности ЭВМ и зависит от её важнейших технических характеристик (системы операций, номинального быстродействия, ёмкости памяти, надёжности, скорости работы устройств ввода-вывода);
и отражает эффективное быстродействие ЭВМ, причём является критерием оценки технической эффективности ЭВМ и зависит от её важнейших технических характеристик (системы операций, номинального быстродействия, ёмкости памяти, надёжности, скорости работы устройств ввода-вывода); – суммарные затраты на изготовление, амортизацию и эксплуатацию ЭВМ за время Т;
– суммарные затраты на изготовление, амортизацию и эксплуатацию ЭВМ за время Т;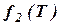 – объём работы, выполненной ЭВМ за время её живучести, в пересчёте на число операций типового набора;
– объём работы, выполненной ЭВМ за время её живучести, в пересчёте на число операций типового набора; измеряются в различных шкалах, то необходимо привести их к единой шкале. Для этого обычно формируют следующий критерий:
измеряются в различных шкалах, то необходимо привести их к единой шкале. Для этого обычно формируют следующий критерий: (1.7)
(1.7)
 (1.8)
(1.8) определяет в пространстве критериев некоторую точку, которую назовём точкой «абсолютного максимума». Если найденные векторы х* в каждой из задач (1.8) различны, то не существует такого выбора, который позволил бы достичь этой точки. Точка
определяет в пространстве критериев некоторую точку, которую назовём точкой «абсолютного максимума». Если найденные векторы х* в каждой из задач (1.8) различны, то не существует такого выбора, который позволил бы достичь этой точки. Точка  является недостижимой в пространстве критериев.
является недостижимой в пространстве критериев. до точки
до точки 

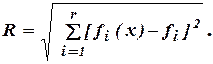 (1.9)
(1.9) . Это значит, что параметры будущего проекта должны быть таковы, чтобы максимизировать функции
. Это значит, что параметры будущего проекта должны быть таковы, чтобы максимизировать функции 
 (1.10)
(1.10) жестко не заданы, то они могут быть определены в результате экспертного опроса.
жестко не заданы, то они могут быть определены в результате экспертного опроса. расположим в порядке убывания важности. В основу построения процедуры упорядоченности может быть положен метод экспертных оценок. Каждый из критериев необходимо максимизировать.
расположим в порядке убывания важности. В основу построения процедуры упорядоченности может быть положен метод экспертных оценок. Каждый из критериев необходимо максимизировать.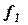 . Затем назначается, исходя из практических соображений и заданной точности, некоторая уступка
. Затем назначается, исходя из практических соображений и заданной точности, некоторая уступка  , которую согласны мы допустить, чтобы обратить вмаксимум второй критерий
, которую согласны мы допустить, чтобы обратить вмаксимум второй критерий 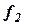 . Накладываем при этом на критерий
. Накладываем при этом на критерий  , где
, где  – максимально возможное значение
– максимально возможное значение  и т. д. До последнего критерия
и т. д. До последнего критерия  .
.
 .
.
 входит в R, т. е.
входит в R, т. е.  , то пишут x R y, что читается: “ x находится в отношении R с y ”.
, то пишут x R y, что читается: “ x находится в отношении R с y ”. .
. ,
,  ,
,  , где
, где 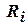 – множество таких пар
– множество таких пар  ,
,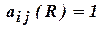 , если выполнено
, если выполнено  ,
, , если не выполнено
, если не выполнено  к элементу
к элементу  проводится дуга тогда и только тогда, когда выполнено
проводится дуга тогда и только тогда, когда выполнено  ) превращается в петлю при вершине
) превращается в петлю при вершине  ).
). таких, что
таких, что  ;
;
 . (1.11)
Аналогично определяется нижнее сечение:
. (1.11)
Аналогично определяется нижнее сечение:
 . (1.12)
. (1.12)
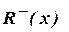 – это множество всех элементов
– это множество всех элементов  находится в отношении
находится в отношении  .
. – это множество всех элементов
– это множество всех элементов  с фиксированным элементом
с фиксированным элементом  называется дополнением отношения
называется дополнением отношения  \
\ 

 (1.13)
где множество
(1.13)
где множество  – n -мерное пространство
– n -мерное пространство  .
.


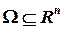 называется множество:
называется множество:
 . (1.14)
. (1.14)
 содержит те и только те элементы х* для которых
содержит те и только те элементы х* для которых  .
. ;
;

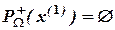 ,
,  ,
, ,
, ,
, ,
,  .
. и
и  .
. , где
, где  и множеству решений х Î Х,
и множеству решений х Î Х,


 Определение 6
Определение 6
 не существует более предпочтительной по Парето точки, т.е. такой точки х, что
не существует более предпочтительной по Парето точки, т.е. такой точки х, что  , тогда
, тогда  называется
эффективным или Парето-оптимальным решением многокритериальной задачи:
называется
эффективным или Парето-оптимальным решением многокритериальной задачи:
 .
.
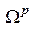 , называется множеством Парето и обозначается
, называется множеством Парето и обозначается  .
. и называется множеством эффективных оценок. Смысл введённого понятия состоит в том, что оптимальный исход следует искать среди элементов множества недоминируемых элементов
и называется множеством эффективных оценок. Смысл введённого понятия состоит в том, что оптимальный исход следует искать среди элементов множества недоминируемых элементов  , оказывающаяся более предпочтительной с учётом всех частных целевых функций
, оказывающаяся более предпочтительной с учётом всех частных целевых функций 



