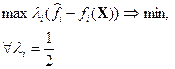Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение на основе лексикографического упорядочения критериевСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Как и в предыдущем подходе, предпочтения ЛПР выявляются до поиска наилучшего решения. Метод применим, если для ЛПР приемлемо ранжирование критериев по важности и при этом предпочтительным является то решение, в котором лучше значение более важного критерия независимо от значения всех менее важных критериев. Лексикографическое отношение 1) 2) ……… m) В этом случае говорят, что вектор Y лексикографически больше вектора Множество векторов (решений), оптимальных по отношению Лексикографически-оптимальное решение достигается в процессе решения следующей последовательности задач: 1) находим 2) находим ..................... m) находим Процесс решения прекращается, как только очередная задача из этой последовательности дает единственное решение. Нетрудно показать, что такая процедура приводит к решению многокритериальной задачи, которое принадлежит парето-оптимальному множеству. В то же время, если остановиться на задаче, имеющей не единственное решение, то нельзя гарантировать, что полученное решение является эффективным (оно может быть слабо эффективным). В случае линейной модели решение последовательности отдельных задач можно объединить в один симплекс-процесс, что значительно снижает трудоемкость решения. Для этого применяют лексикографический вариант симплекс-метода. В этом методе каждому критерию соответствует своя строка относительных оценок
Методы главного критерия, свертки, идеальной точки, целевого прогр. Метод главного критерия Суть метода состоит в том, что ЛПР выделяет главный критерий (далее f 1(X)), а на остальные критерии накладывает требования, что они были не меньше задаваемых им минимальных (пороговых) значений t i. Тогда многокритериальная задача сводится к однокритериальной задаче
Если эта задача разрешима, то ее решение всегда является слабо эффективным, а если оно единственно, то и эффективным. Заметим, что этот вывод не зависит от выбора главного критерия. Рис.10.7 иллюстрирует случай единственного решения задачи (10.16), а рис.10.8 – множества оптимальных решений, лежащего на границе ab, из которого только точка а является эффективной. Практически задачу (10.16) решают для нескольких наборов значений { ti }, и затем на основании анализа полученных (слабо) эффективных решений ЛПР определяет наиболее предпочтительное из них.
Рассмотренный метод целесообразно применять, когда ЛПР может обоснованно назначить значения ti или указать узкие пределы для них. Линейная свертка Если ЛПР может не только ранжировать критерии, но и дать сравнительную количественную оценку значимости (важности) критериев, решение многокритериальной задачи сводится к обычной задаче с одним критерием, в качестве которого берется обобщенный показатель вида
где Сi - положительные числа, отражающие веса критериев в структуре предпочтений ЛПР. При групповом ЛПР Ci находятся по индивидуальным весам одним из методов обработки экспертных оценок. Обычно значения Сi нормируются так, чтобы Данный способ решения многокритериальной задачи имеет существенные недостатки. Во-первых, большие затруднения возникают при определении весов. Одно дело – расположить критерии по важности, и совсем другое - оценить на сколько или во сколько один критерий важнее другого. Во-вторых, неизвестна связь между значениями весов и значениями критериев в точке максимума F (Х). Очень часто эта зависимость оказывается существенно нелинейной (даже в линейных задачах), включая зоны нечувствительности значений fi к изменению Ci. Поэтому для получения решения, удовлетворяющего ЛПР, приходится максимизировать F (X) для нескольких наборов С i. Наконец, заметим, что в свертке (10.17) целесообразно все критерии приводить к одним единицам измерения. С этой целью лучше представлять критерии в относительных единицах, беря за базовое максимальное или желаемое значение. Достоинство метода – в стандартности задачи, к которой сводится исходная многокритериальная проблема. Пример 10.1. Рассмотрим задачу линейного программирования с тремя критериями: максимизировать f 1(X) =- 3 x 1 + 2 x 2, f 2(X) = 4 x 1 + 3 x 2, f 3(X)=2 x 1 - 5 х 2 при условиях 2 x 1 + 3 x 2 2 x 1+ x 2 x 1, x 2 Допустимая область и линии равного уровня критериев показаны на
то результат максимизации F (Х), как легко убедиться, совпадает с максимизацией одной функции f 3(Х).Таким образом, при равных весах решение по линейной свертке дает наилучшее значение f 3 и наихудшее для f 1. Используя параметрическое программирование, можно определить диапазон значений Ci (зону нечувствительности), в котором оптимальное решение по F (Х) будет оставаться в точке С. Максиминная свертка Как и в предыдущем подходе, ЛПР должен задать веса Ci всем критериям, но обобщенный критерий записывается в виде F(X)= Тогда многокритериальная задача сводится к максимизации F (X) на Х F (Х )=х о
X который более удобен для решения. В частности, если в исходной задаче все функции линейны, то и задача в виде (10.19) будет обычной задачей линейного программирования. Функция (10.18) подпадает под действие теоремы 5, что гарантирует получение, по крайней мере, слабо эффективного решения многокритериальной задачи. Максиминная свертка имеет те же недостатки, что и предыдущая, но отличается тем, что максимально увеличивает минимальное слагаемое в (10.17), способствуя относительному сближению значений критериев. Пример 10.2. Применим рассмотренный подход к задаче из примера 10.1. Снова возьмем равные веса. В соответствии с (10.19) к исходным условиям задачи добавятся ограничения -3 x 1+2 x 2 4 x 1+3 x 2 2 x 1-5 x 2 и новый критерий х0 Сравним с результатами примера 10.1. При решении по критерию (10.17) получили Метод идеальной точки Идеальной или точкой абсолютного максимума называют точку в критериальном пространстве, в которой все критерии достигают своих максимальных значений:
где р может быть любым целым положительным числом и
где Как и ранее, целесообразно использовать отклонения в относительных единицах, для чего выражение в квадратных скобках в (10.20) можно разделить на Пример 10.3. Найдем решение для модели из примера 10.1 при одинаковых
После отбрасывания общего множителя (1/3), свободного члена (820) и простых преобразований приходим к выражению
Используя метод квадратичного программирования, получаем: х Метрика с р =
которое следует минимизировать по X Пример 10.4. Если воспользоваться сверткой (10.21) для модели из примера 10.1, то получим решение: х Пример 10.5. Пусть требуется максимизировать два критерия f 1 ( X )=- 2 x 1 +x 2,, f 2 ( X )= 4 x 1- x 2 при условиях x 1 +x 2 -x 1 +x 2 0
Решения этой задачи, полученные при различных способах свертки, сведены в следующую таблицу.
Здесь квадратными скобками обозначены интервалы, соответствующе множеству решений, оптимальных по данному обобщенному критерию. Как видно из таблицы, линейная свертка с равными весовыми коэффициентами (строка 3) дает весьма однобокий результат: значения второго критерия лежат в области максимума, а первого – в области минимума. Максиминная свертка дала равные абсолютные значения критериев, но второй критерий сильнее, чем первый, отличается от своего максимально возможного значения (строка 4). Очевидно, если использовать в этой свертке относительные величины критериев, взяв за базу, например, разность (max fi -min f i), то можно ожидать более "справедливого" соотношения значений критериев в оптимальном решении. Действительно, максимизация минимальной относительной величины критерия с весовым коэффициентом приводит к увеличению f 2 и уменьшению f 1 (строка 5). Следующие два решения, представленные в 6 и 7 строках таблицы, минимизируют отклонения от идеальной точки I. Результат, соответствующий минимуму суммы квадратов отклонений. можно получить геометрически. Так при одинаковых значениях Таким образом, все способы свертки дают решения, принадлежащие паретовскому множеству, которое лежит на ломаной КЕСВА (рис.10.11).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.012 с.) |

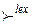 определяется следующим образом. Для двух векторов
определяется следующим образом. Для двух векторов  и
и 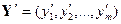 имеет место отношение
имеет место отношение  тогда и только тогда, когда выполняется одно из условий:
тогда и только тогда, когда выполняется одно из условий: >
> 
 >
>  (10.15)
(10.15)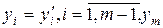 >
>  .
. .
.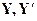 либо один лексикографически больше другого, либо они равны, то множество Optlex Y, если оно не пустое, содержит только один элемент. Так на множестве G, изображенном на рис.10.3, лексикографически оптимальной является только точка h.
либо один лексикографически больше другого, либо они равны, то множество Optlex Y, если оно не пустое, содержит только один элемент. Так на множестве G, изображенном на рис.10.3, лексикографически оптимальной является только точка h. при условии
при условии  ;
; при условии
при условии  ;
; при условии
при условии  .
. (i-индекс критерия, j- индекс переменной). Строки располагаются в порядке убывания приоритетов критериев. Сначала симплекс-преобразования выполняются по
(i-индекс критерия, j- индекс переменной). Строки располагаются в порядке убывания приоритетов критериев. Сначала симплекс-преобразования выполняются по  . При достижении оптимального решения по 1-му критерию (
. При достижении оптимального решения по 1-му критерию ( ) выявляют нулевые оценки небазисных переменных. Если таких нет, то решение единственное и лексикографическая оптимизация завершается. Если они есть, то в строке
) выявляют нулевые оценки небазисных переменных. Если таких нет, то решение единственное и лексикографическая оптимизация завершается. Если они есть, то в строке  в столбцах с выделенными нулевыми
в столбцах с выделенными нулевыми  а
а  <0, вводится в базисное решение, улучшая значение 2-го критерия без ухудшения значения 1-го критерия. Этот процесс продолжается, пока будут выявляться такие перспективные переменные. Если они исчерпались или их не было, то переходят к решению по 3-му критерию, т.е. к выбору перспективных переменных по строке
<0, вводится в базисное решение, улучшая значение 2-го критерия без ухудшения значения 1-го критерия. Этот процесс продолжается, пока будут выявляться такие перспективные переменные. Если они исчерпались или их не было, то переходят к решению по 3-му критерию, т.е. к выбору перспективных переменных по строке  . Введение в решение небазисной переменной хр улучшит значение 3-го критерия без изменения первых двух, если
. Введение в решение небазисной переменной хр улучшит значение 3-го критерия без изменения первых двух, если  а
а  <0. Процесс решения многокритериальной задачи завершается, когда на последующих этапах не находятся перспективные переменные.
<0. Процесс решения многокритериальной задачи завершается, когда на последующих этапах не находятся перспективные переменные. (10.16)
(10.16)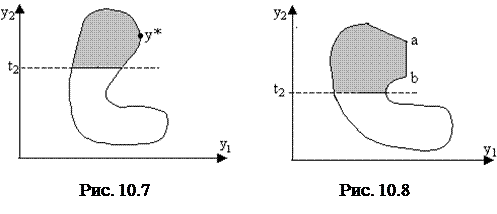
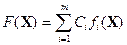 , (10.17)
, (10.17)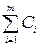 =1. Как следует из теоремы 5, точка максимума функции (10.17) при положительных Сi является эффективной.
=1. Как следует из теоремы 5, точка максимума функции (10.17) при положительных Сi является эффективной. 18,
18, 0.
0. =18,
=18, 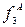 =-30; max f 2(X)=24 в точке В(3,4), где
=-30; max f 2(X)=24 в точке В(3,4), где  =-1 и
=-1 и 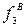 =-14; mах f 3(Х)=10 в точке С(5,0), в которой
=-14; mах f 3(Х)=10 в точке С(5,0), в которой  =-15 и
=-15 и  =20. Если взять свертку с равными весами, то есть
=20. Если взять свертку с равными весами, то есть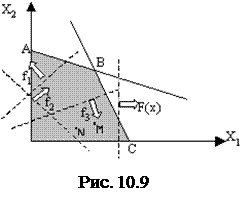

 . (10.I8)
. (10.I8) D. Если ввести новую переменную х о, то эта задача преобразуется к виду
D. Если ввести новую переменную х о, то эта задача преобразуется к виду max;
max; х о, i =
х о, i =  ; (10.19)
; (10.19)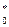 =х
=х  =х
=х  = 0, в которой f 1, f 2 и f 3 тоже равны нулю.
= 0, в которой f 1, f 2 и f 3 тоже равны нулю. fi=-15, а по критерию (10.18)
fi=-15, а по критерию (10.18)  .
. Если эта точка принадлежит достижимому множеству G, то все эффективное (паретовское) множество состоит из этой единственной точки (рис. 10.10) и проблемы как таковой в этом случае нет. Однако идеальная точка обычно лежит вне множества G и поэтому нереализуема. В связи с этим ее иногда называют также утопической. Идея метода состоит в том, чтобы на множестве G найти точку, наиболее близкую к идеальной. Мерой близости выступает некоторая функция расстояния
Если эта точка принадлежит достижимому множеству G, то все эффективное (паретовское) множество состоит из этой единственной точки (рис. 10.10) и проблемы как таковой в этом случае нет. Однако идеальная точка обычно лежит вне множества G и поэтому нереализуема. В связи с этим ее иногда называют также утопической. Идея метода состоит в том, чтобы на множестве G найти точку, наиболее близкую к идеальной. Мерой близости выступает некоторая функция расстояния  , в качестве которой используют в общем случае взвешенные Lp -метрики
, в качестве которой используют в общем случае взвешенные Lp -метрики ,
, . Так как возведение в степень
. Так как возведение в степень  является монотонным преобразованием, то на положение экстремума оно не влияет. Таким образом, многокритериальная задача сводится к минимизации функции
является монотонным преобразованием, то на положение экстремума оно не влияет. Таким образом, многокритериальная задача сводится к минимизации функции (10.20)
(10.20)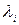 - веса отклонений, задаваемые ЛПР (
- веса отклонений, задаваемые ЛПР (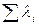 =1,
=1,  .
. =12,
=12,  =24 и
=24 и  =10, обобщенный критерий запишется в соответствии с (10.20) в виде
=10, обобщенный критерий запишется в соответствии с (10.20) в виде .
. .
. , (10.21)
, (10.21)