
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение открытой транспортной задачи к закрытойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В открытой или несбалансированной задаче имеет место неравенство
Прежде чем решать такую задачу, необходимо привести ее к сбалансированному виду. В зависимости от ситуации сбалансировать задачу можно формальным способом без обращения к ЛПР или с привлечением дополнительной информации от ЛПР. Рассмотрим формальные приемы. Пусть в исходной задаче предложение превышает спрос:
Тогда условия задачи имеют вид
В каждое неравенство (5.22) введем дополнительную переменную xi,n+1. В сумме эти переменные должны равняться величине дебаланса:
Добавляя это равенство к условиям (5.23), получаем закрытую задачу:
Потребность bn+1 называют фиктивной.Таким образом, чтобы сбалансировать задачу, достаточно ввести фиктивного потребителя с потребностью, равной дебалансу. Практически это означает, что к исходной таблице добавляется один столбец с потребностью bn+1 и затратами Ci,n+1 =0. Ненулевые дополнительные переменные в оптимальном решении будут показывать количество груза, остающееся в соответствующих ПО. Второй случай несбалансированности задачи имеет место, когда спрос превышает предложение:
При этом исходные условия записываются в виде:
Поступаем аналогично первому случаю. Введем в каждое неравенство дополнительную переменную xm+ 1, j. Очевидно, что сумма этих переменных равна величине дебаланса:
С учетом этого равенства сбалансированная модель принимает вид:
Такое преобразование соответствует введению фиктивного поставщика (дополнительной строки) с возможностью am+ 1 и нулевыми затратами Cm+ 1, j. Дополнительная переменная xm+ 1, j имеет смысл количества груза, недопоставленного j- му ПН. Рассмотренный формальный способ будет неприемлем, если потребители по-разному реагируют на недопоставки. Тогда возможны два варианта решения задачи: 1. ЛПР корректирует потребности, обеспечивая баланс. 2. Выявляется и учитывается влияние недопоставок для каждого потребителя. Если зависимость потерь от величины недопоставки линейная, то задача остается в классе линейных. В этом случае задача балансируется как при формальном подходе, но в дополнительной строке в качестве затрат берутся удельные потери от недопоставки. Если ожидается, что спрос будет длительное время превышать существующие возможности на величину am+ 1, то встает вопрос о расширении производства. Он может решаться в рамках транспортной модели следующим образом. Проектируются варианты увеличения производства, каждый на величину am+ 1. В исходную таблицу добавляется столько строк, сколько предлагается вариантов. При k вариантах это приведет к противоположному дебалансу, равному (k –1)· am+ 1. Поэтому для сбалансированности модели добавляется фиктивный потребитель с такой потребностью. А в качестве затрат во всех клетках таблицы принимаются суммарные затраты на перевозку и производство С’ij=Cij+Ci, где Ci – себестоимость в i -м ПО. Исключение составляет фиктивный столбец: в первых m клетках затраты равны M, а в остальных – нулю. Те варианты, которые в оптимальном решении закрепятся за фиктивным потребителем, должны быть отброшены.
При прогнозировании длительного превышения возможностей над спросом может возникнуть вопрос о сокращении производства. Он также может быть представлен в виде транспортной задачи. Достаточно в затраты включить себестоимость, как в предыдущем случае, и добавить фиктивного потребителя с потребностью bn+1 и нулевыми затратами.Оптимальные значения дополнительных переменных в фиктивном столбце дадут величину сокращения производства в соответствующих ПО с учетом полных затрат. 27. Транспортные задачи в сетевой постановке Транспортную задачу можно представить в виде ориентированного графа с одним истоком (в него не входит ни одна дуга) и с одним стоком (из него не выходят дуги), который называют в этом случае сетью. Вершинам графа ставятся в соответствие пункты отправления, назначения и промежуточные пункты. Основной параметр вершины – количество груза. Дуги отображают коммуникации. Им могут быть приписаны такие параметры как количество груза, затраты на перевозку, пропускная способность.
Исходный граф транспортной задачи легко сводится к сети с одним стоком и одним истоком путем введения фиктивных пунктов t (исток) и s (сток). Фиктивным дугам приписываются значения параметров: dti=ai, djs=bj, Cti=Cjs =0. Пример сети транспортной задачи без промежуточных пунктов приведен на рис. 5.6. Модель Тd-задачи в сетевой постановке имеет вид:
åå Cijxij ®min; (5.29)
В сбалансированной транспортной задаче Z =å a i=å bj; (5.32) 0£ xij £ dij. (5.33) Равенства (5.30) отражают условия баланса для всех пунктов кроме источника и стока. Баланс для последних представлен уравнением (5.31). В модели использованы обозначения: Наибольший интерес представляет постановка задачи, в которой критерием является поток сети: Z ® max; (5.34)
0£ xij £ dij. (5.37) Задача (5.34) – (5.37) называется задачей о максимальном потоке. Она имеет большое практическое значение. Для нее разработаны алгоритмы, которые эффективнее методов решения транспортных задач. Они работают непосредственно с сетью как разновидностью графов. В связи с этим напомним понятие разреза графа (сети), которое используется в основополагающей теореме Форда-Фалкерсона. Пусть дан ориентированный граф G= (V,U), где V и U -множества вершин и дуг соответственно. Разрезом сети на подмножестве вершин A Ì V, A ¹Æ, A ¹ V, tÎ A, sÎ V\A называется множество дуг ij Î U таких, что i Î A & j Î V\A. Обозначим его P(A). Сумма пропускных способностей дуг разреза называется величиной (пропускной способностью) разреза:
Пример 5.5. Построим один из разрезов сети, приведенной на рис.5.7.
Разрез сети, имеющий минимальную пропускную способность, называется минимальным разрезом. Можно показать, что задачи максимизации потока и минимизации величины разреза являются двойственной парой. Из этого факта следует Величина потока сети (от истока к стоку) не превосходит пропускной способности минимального разреза и существует максимальный поток, величина которого равна пропускной способности минимального разреза. Методы решения задачи о максимальном потоке основаны на последовательном увеличении потока при соблюдении условий (5.35)-(5.37). При этом легко увидеть аналогию с перемещением по циклу в методах решения транспортных задач. Аналогом цикла пересчета является увеличивающая цепь. Это цепь, соединяющая исток и сток, все дуги которой допустимые. Дуга является допустимой увеличивающей, если ее направление совпадает с направлением потока и поток на ней меньше пропускной способности, то есть xij<dij. Дуга считается допустимой уменьшающей, если направление дуги противоположно потоку и xij > 0. На увеличивающей дуге поток может возрасти на величину qij=dij-xij, а на уменьшающей дуге возможно снижение потока, равное qij = xij. Следовательно, максимальное допустимое изменение величины потока по увеличивающей цепи определяется как минимальное из возможных: q0 = Таким образом, максимальный поток сети может быть определен по следующему алгоритму. 1. Задать начальную величину потока, обеспечиваемую потоками дуг при выполнении условий (5.35)-(5.37). Примечание. Очевидно, что в качестве начального всегда можно взять нулевой поток. 2. Построить увеличивающую цепь. Если построить невозможно, то решение завершено. 3. По формуле (5.38) вычислить q0. 4. Переместить вдоль цепи q0, прибавляя к потокам на увеличивающих дугах и вычитая из потоков уменьшающих дуг. В результате поток сети увеличивается на q0. Перейти на шаг 2.
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.124 (0.01 с.) |

 .
.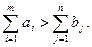
 (5.22)
(5.22) (5.23)
(5.23)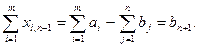

 .
.

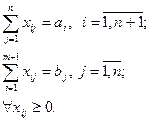

 k ¹ t, k ¹ s; (5.30)
k ¹ t, k ¹ s; (5.30) (5.31)
(5.31) – множество дуг, входящих в вершину k и выходящих из нее, Z – новая величина, называемая потоком сети.
– множество дуг, входящих в вершину k и выходящих из нее, Z – новая величина, называемая потоком сети.
 Если A ={t,1,2,3}, то разрезом будет множество дуг P(A)={1,4; 1,6; 2,5; 3,6}, а его величина определяется как d (A)= d14+d16+d25+d36. Дуги, составляющие этот разрез, выделены жирными линиями.▲
Если A ={t,1,2,3}, то разрезом будет множество дуг P(A)={1,4; 1,6; 2,5; 3,6}, а его величина определяется как d (A)= d14+d16+d25+d36. Дуги, составляющие этот разрез, выделены жирными линиями.▲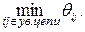 (5.38)
(5.38)


