
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Здесь приводится только один из наиболее часто используемых методов – метод ньютона – рафсона.Содержание книги
Поиск на нашем сайте Он основан на линейной аппроксимации первой производной минимизируемой функции f в окрестности текущей точки xk:
В стационарной точке аппроксимации, которая принимается за очередное приближение xk+ 1, производная равна нулю:
Отсюда следует рекуррентная формула для построения последовательности приближений к искомому минимуму:
Очевидно, что применение (8.41) возможно только при условии, что В общем случае процедура (8.41) не гарантирует сходимость к стационарной точке. Если начальная точка достаточно близка к стационарной, то метод сходится. При сходимости обеспечивается высокая скорость приближения к минимуму. На рис. 8.14 приведен случай сходимости метода. Очередному приближению соответствует точка пересечения оси x аппроксимирующей прямой. Как видно, последовательность точек x 0, x 1, x 2,… приближается к минимуму x*.
Многомерный поиск безусловного минимума Здесь рассматриваются методы прямого поиска (разд. 8.8.1, 8.8.2 и 8.8.3), градиентные методы (разд.8.8.4), метод второго порядка, алгоритмы случайного поиска и приводятся краткие сведения о других методах. 8.8.1. Метод Гаусса-Зейделя (покоординатного спуска) Процедура поиска сводится к решению последовательности задач одномерной минимизации по каждой переменной. Пусть выбрана начальная точка
Зафиксируем все переменные, кроме первой, на начальных значениях и решаем задачу
одним из одномерных методов. Фиксируем х 1 на полученном в решении значении x1' и делаем свободной переменную х 2. Приходим к очередной одномерной задаче
Аналогично строятся и решаются последующие одномерные задачи, последняя из которых имеет вид:
Эти n задач составляют один цикл. Его результатом является точка X1. Она принимается за начальную точку для следующего аналогичного цикла. Поиск заканчивается, когда расстояние между двумя последовательными точками становится меньше заданной величины:
Работу метода иллюстрирует рис. 8.16, на котором показана траектория поиска минимума функции f= (2- x 1)4+2(x 1-2 x 2)2.
Метод Хука-Дживса (метод конфигураций) Метод первого порядка Он применим к дифференцируемым функциям в случаях, когда первая производная может вычисляться с высокой точностью. Рассматриваемый метод средней точки алгоритмически является самым простым из методов одномерной оптимизации на заданном интервале. Он заключается в определении средней точки интервала c= (a+b) / 2 и вычислении в ней производной. Если f ' (c) < 0, полагают а = с, при f ' (c) > 0, принимают b = с. Условие окончания поиска учитывает точность по координате e и по производной функции e 1: ((b-a)< e) & (| f ' (c) | < e 1). Эффективность метода зависит от трудоемкости вычисления производной. Задаваемая точность e 1 не дожна быть выше точности вычисления производной. С ростом трудоемкости и снижением точности вычислений производной следует отдавать предпочтение прямым методам. Методы второго порядка Методы применимы к дважды дифференцируемым функциям. При этом предъявляются высокие требования к точности вычисления производных. Наиболее удачными считаются задачи, в которых известно аналитическое выражение первой производной, а еще лучше – и второй.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |


 .
. (8.41)
(8.41) для каждого k. Поиск завершается по условию достижения точности, заданной величиной первой производной | f ' (xk) | < e 1 или расстоянием между двумя точками | xk+ 1- xk | < e. Возможно одновременное использование этих условий.
для каждого k. Поиск завершается по условию достижения точности, заданной величиной первой производной | f ' (xk) | < e 1 или расстоянием между двумя точками | xk+ 1- xk | < e. Возможно одновременное использование этих условий.
 Для некоторых функций результат поиска зависит от выбора начальной точки. Так, например, при начальной точке, взятой правее максимуму производной, так как показано на рис. 8.15, метод расходится.
Для некоторых функций результат поиска зависит от выбора начальной точки. Так, например, при начальной точке, взятой правее максимуму производной, так как показано на рис. 8.15, метод расходится. .
.
 .
. .
.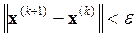 .
.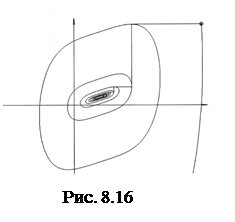



 Из анализа траекторий поиска в приведенных примерах можно заключить, что эффективность поиска повысится, если к описанным однотипным циклам добавить движение в направлении, проходящем через точки X( k ) и X( k +1). Это движение называют ускоряющим шагом. Он используется в методе, рассматриваемом в следующем разделе.
Из анализа траекторий поиска в приведенных примерах можно заключить, что эффективность поиска повысится, если к описанным однотипным циклам добавить движение в направлении, проходящем через точки X( k ) и X( k +1). Это движение называют ускоряющим шагом. Он используется в методе, рассматриваемом в следующем разделе.


