
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Снижение размерности с помощью множителей ЛагранжаСодержание книги
Поиск на нашем сайте Покажем на примере задачи 1, каким образом введение множителей Лагранжа позволяет заменить исходную задачу рядом задач с меньшей размерностью вектора состояния. В задаче 1 состояние описывалось двумя параметрами, что обусловливалось наличием двух ограничений. Для уменьшения размерности на 1 достаточно из модели (9.40)-(9.43) убрать одно из ограничений, что можно сделать, если удаляемое ограничение включить в критерий задачи с неопределенным множителем Лагранжа l. Тогда модель измененной задачи примет вид:
Как будет доказано ниже, задача (9.52)-(9.54) при определенных условиях эквивалентна исходной задаче (9.40)-(9.43). Так как ограничения (9.53), (9.54) не связывают между собой переменные yj, то есть они стали независимыми, то справедлива следующая цепочка равенств:
где
Функции hj (xj) имеют смысл, если максимум в (9.55) достигается при конечных значениях yj, что всегда будет, когда
Это условие ограничивает применение данного способа, но в рассматриваемой задаче оно, очевидно, выполняется, так как при неограниченном возрастании ресурса y рост прибыли будет замедляться. Как видно из (9.55), вычисление функции hj (xj) при фиксированном значении
Получили уже знакомую нам задачу распределения одного ресурса. Для решения ее методом ДП введем последовательность функций
где V - параметр состояния, значения которого не превосходят X. Для них справедливо рекуррентное соотношение: fk (V) = max[ hk (xk)+ fk -1(V - xk)], (9.60) в котором f 1(V)= h 1(V), Вычисления по формуле (9.60) проводятся, как обычно, от f 1 к fN, затем в обратном порядке - безусловная оптимизация, начиная с V = X, которая дает значения Нетрудно увидеть, что оптимальное решение измененной задачи зависит от принятого значения множителя Чтобы нагляднее представить весь расчет с использованием множителей Лагранжа, приведем его алгоритм в виде блок-схемы (рис.9.11). Как видно из алгоритма, функции fk (V) и hj (xj), участвующие в расчете, зависят от одного параметра состояния, и, следовательно, поставленная цель достигнута.
Рис.9.11 Теперь покажем эквивалентность задач (9.40)-(9.43) и (9.52)-(9.54), понимая под этим совпадение решений. Следуя Беллману, доказательство проведем от противного. Имея оптимальное решение измененной задачи
Так как е
Но здесь и слева, и справа имеем выражение критерия измененной задачи, по которому оптимальным является решение Для задачи 2 применение метода множителей Лагранжа реализуется проще. Модель измененной задачи можно записать по аналогии с вышеприведенным случаем в виде:
Для функций последовательности, определенных как
справедливо следующее рекуррентное соотношение
Как видно, здесь нет дополнительных функций hj и вычисления можно проводить сразу по рекуррентной формуле (9.63), задавшись предварительно значением В общем случае, когда вектор состояния исходной задачи имеет размерность m, можно использовать q множителей Лагранжа (q < m), что позволит снизить размерность вектора состояния измененной задачи до m-q. При этом выполнение исключенных из условий исходной задачи q ограничений может быть обеспечено управлением таким же числом множителей Лагранжа. Однако увеличение размерности вектора состояния и соответственно числа множителей Лагранжа ведет к значительно более быстрому росту трудоемкости решения измененной задачи. Поэтому проблема "проклятия размерности" остается, ограничивая применение метода ДП задачами с небольшим числом параметров состояния. Несмотря на указанный недостаток метод динамического программирования находит широкое применение для решения многих задач исследования операций, в том числе задач распределения, замены, кратчайшего пути, упорядочения и др.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

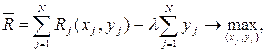 (9.52)
(9.52) (9.53)
(9.53) (9.54)
(9.54)
 . (9.55)
. (9.55) . (9.56)
. (9.56) заключается в нахождении максимума функции одной переменной для всех возможных значений xj, что не вызывает особых затруднений (для дифференцируемых Rj (xj, yj) максимум можно найти аналитически). При известных hj (xj), j =1, N задача (9.52)-(9.54) сводится к следующей:
заключается в нахождении максимума функции одной переменной для всех возможных значений xj, что не вызывает особых затруднений (для дифференцируемых Rj (xj, yj) максимум можно найти аналитически). При известных hj (xj), j =1, N задача (9.52)-(9.54) сводится к следующей: (9.57)
(9.57) (9.58)
(9.58)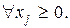 (9.59)
(9.59)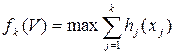 ,
, = V.
= V.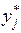 . Теперь следует вспомнить об условии (9.42), которое не вошло в измененную задачу. Если å
. Теперь следует вспомнить об условии (9.42), которое не вошло в измененную задачу. Если å  ,
, 
 ,
,  . Тогда для критерия исходной задачи должно выполняться неравенство
. Тогда для критерия исходной задачи должно выполняться неравенство . (9.61)
. (9.61) . (9.62)
. (9.62)



 (9.63)
(9.63) )Ј B и, если оно не выполняется, то необходимо изменить значение
)Ј B и, если оно не выполняется, то необходимо изменить значение 


