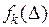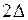Распределение одного вида ресурса

Пусть необходимо распределить ресурс в количестве X между N предприятиями, если известно, что при выделении i -му предприятию ресурса x_i оно дает прибыль r_i (x_i). При этом к функциям r_i не предъявляется каких-либо требований (например, дифференцируемости).

Запишем модель задачи:

. (9.7)

Очевидно, что условия применимости ДП выполняются: и критерий, и ограничение задачи (9.7) являются составными (в данном случае - аддитивными). Представим задачу как многошаговую. В качестве шага будем рассматривать выделение ресурса одному предприятию. Расположим предприятия в виде последовательности, в которой каждому предприятию приписано определенное место, и пронумеруем их справа налево. Порядок предприятий в последовательности шагов принципиального значения не имеет, но могут оказаться полезными следующие советы:

1. Если условие-ограничение имеет вид равенства, то на 1-е место целесообразно ставить предприятие с наиболее сложной функцией прибыли, а при неравенстве - наоборот, с самой простой, так как в этом случае несколько снизится трудоемкость расчетов.

2. Если нет уверенности, что некоторое предприятие останется в рассматриваемой системе распределения, его следует поставить последним (на самое левое место); тогда в случае его удаления не придется решать задачу заново.

Теперь необходимо определиться с состоянием. Для этого зададимся вопросом: что нужно знать, чтобы принять решение по распределению ресурса между заданным числом предприятий? Ответ очевиден - количество распределяемого ресурса. Тот же ответ последует и на вопрос: от чего зависит максимальная прибыль системы предприятий в нашей задаче? Следовательно, состояние определяется одним параметром - количеством распределяемого ресурса, которое обозначим через V. Оно может относиться к разному числу предприятий, поэтому VЈX. В соответствии с процедурой ДП введем последовательность функций { f_k (V_k)} так, что

(9.8)

есть максимальная прибыль k предприятий при распределении между ними ресурса в количестве V_k.

Если бы пришлось искать функции (9.8) непосредственно, то потребовалось бы решать семейство задач вида

(9.9)

для 0 Ј V Ј X, что многократно увеличивает трудоемкость решения. В динамическом программировании число задач будет таким же, однако их размерность не зависит от номера задачи и будет в N раз меньше размерности исходной задачи.

Перейдем к составлению рекуррентного соотношения. Допустим, что осталось распределить ресурс V_k между k предприятиями. Выделим из них две части: k -е предприятие и все остальные k -1 (рис.9.8).

 

Примем решение по k -му предприятию: из всего имеющегося ресурса V_k выделим ему X_k. Тогда оно даст прибыль r_k (x_k), а система перейдет в состояние V_{k -1}, относительно которого следует искать решения на k -1 оставшихся шагах. Согласно принципу оптимальности эти решения должны составлять оптимальное поведение независимо от того, как система попала в состояние V_{k -1}. Такое поведение обеспечит максимальную прибыль от k -1 предприятий, то есть f_{k -1}(V_{k -1}). В результате, прибыль k предприятий составит

r_k (x_k) + f_{k -1}(V_{k -1}). (9.10)

Как следует из модели задачи (9.9), уравнение состояния имеет простой вид

V_{k -1}= V_k - x_k,(9.11)

что означает уменьшение распределяемого ресурса после выделения x_k ресурса k -му предприятию. Подставив (9.11) в (9.10), получим зависимость только от одной переменной x_k:

r_k (x_k) + f_k (V_k - x_k),

максимизация которой по x_k в допустимой области обеспечивает максимальную прибыль от всех k предприятий при распределении ресурса в количестве V_k. Но по определению (9.8) это есть f_k (V_k). Таким образом, приходим к искомому рекуррентному соотношению

. (9.12)

Здесь видно, как допустимая область D_k, задаваемая диапазоном x_k, явно зависит от состояния V_k. Формула (9.12) применима для k і2. Для первой функции последовательности в соответствии с ограничением модели (9.7) и определением (9.8) имеем

f ₁(V ₁)= r ₁(V ₁), x ₁^*= V ₁,

так как весь имеющийся ресурс распределяется полностью. Поэтому 1-й шаг условной оптимизации состоит в прямом вычислении значений заданной функции r ₁, а в ряде случаев и этого не требуется.

Остановимся на вычислительной стороне формулы (9.12). В отдельных случаях при простых функциях r_k (V_k) максимум в (9.12) может быть найден аналитически, однако в общем случае максимум находится одним из численных методов, в том числе полным перебором допустимых значений x_k. Тогда, если x_k и V_k - непрерывные величины, для вычислений по рекуррентному соотношению их необходимо дискретизировать. Шаг дискретности D выбирается по точности, с которой следует провести распределение ресурса. При этом, исходя из уравнения состояния, в данной задаче шаг дискретности должен быть одинаковым для x_k и V_k. С учетом этого рекуррентная формула (9.12) примет вид

(9.13)

где = 1,2,…, m; m D = X, D = V_k, m D = x_k. Один из способов вычислений по формуле (9.13) состоит в том, что сначала фиксируется , а затем ищется максимум правой части, и так для всех значений . Результаты заносятся в таблицу вида

 

 

где x_k ^*( D ) - значение x_k, доставляющее максимум в (9.13) при V_k = D. Все N таблиц, получаемых при последовательном расчете функций f_k, имеют одинаковую структуру. Решение исходной задачи (9.7) находится на этапе безусловной оптимизации следующим образом. По значению V_N = X входим в таблицу N, из которой берем f_N (X) - максимальную прибыль от N предприятий при распределении между ними ресурса в количестве X и x_N ^*= x_N ^*(X) - количество ресурса, выделяемое N -му предприятию при оптимальном распределении ресурса X. По уравнению состояния (9.11) находим V_{N -1}= X - x_N ^*, входим по этому значению состояния в таблицу N -1 и из нее извлекаем f_{N -1}(X - x_N ^*) и x_{N -1} ^* - максимальную прибыль от N -1 предприятий и количество ресурса, выделяемое (N -1)-му предприятию при оптимальном распределении, соответственно. Снова пересчитываем состояние

V_{N -2}= V_{N -1}- x_{N -1}^*= X - x_N ^*- x_{N -1}^*
и по нему входим в таблицу N -2, в которой найдем x_{N -2} ^*, и так вплоть до таблицы 1, из которой получим x ₁^*. В результате имеем оптимальное решение задачи распределения ресурса в количестве X.

На примере этой задачи отметим ряд достоинств метода ДП.

1. Задача содержит N переменных, которые после дискретизации могут принимать m значений. Поэтому порядок числа вариантов распределения определяется величиной m^N (точное значение можно получить, если убрать варианты, не удовлетворяющие условию в (9.7)). При расчете по рекуррентной формуле максимум ищется для m значений состояния, а поиск максимума путем просмотра всего диапазона переменной требует перебора от двух до m +1 вариантов, то есть в среднем ~ m /2. Значит, один шаг включает расчет m ²/2 вариантов, а вся задача в ДП - Nm ²/2. Очевидно, что Nm ²/2<< m^N. Кроме того, вариант в полном переборе требует выполнения большего числа операций (вычисления N функций r (V) и N -1 сложений). Так, например, при m = N =10 полный перебор требует расчета ~10¹⁰ вариантов, что даже при затратах машинного времени порядка 10^-5 секунды на вариант потребует непрерывной работы ЭВМ в течение 277 часов. Для решения этой же задачи методом ДП достаточно рассчитать не более 500 вариантов (!).

2. В случае изменения количества распределяемого ресурса метод полного перебора и другие регулярные численные методы требуют решать задачу заново. В динамическом программировании, если новое значение не больше X, достаточно провести безусловную оптимизацию, взяв за исходное состояние новое значение ресурса. А, как показано выше, безусловная оптимизация требует минимума элементарных действий. Это же возможно и при увеличении ресурса, если с самого начала решения задачи методом ДП увеличить значение X до максимально ожидаемого уровня либо дополнить часть последних таблиц недостающими строками.

3. При использовании любого метода оптимизации, кроме ДП, исключение одного из предприятий из системы распределения приведет к необходимости решать изменившуюся задачу как новую. В динамическом программировании, если этому предприятию был присвоен номер N, то есть оно было последним по ходу условной оптимизации, решение измененной задачи находится сразу: по заданному количеству распределяемого ресурса входим не в N -ю, а в (N -1)-ю таблицу и далее действуем в соответствии со схемой безусловной оптимизации, которая была рассмотрена выше.

Свойства, приведенные в п.п.2,3, обусловлены тем, что несмотря на резкое сокращение числа рассчитываемых вариантов, метод ДП находит не один оптимум для заданных X и N, а оптимумы для всех возможных состояний в данной задаче для принятого порядка нумерации предприятий и соответствующие им оптимальные решения. Иначе говоря, метод ДП дает весь ансамбль оптимальных решений, свойственных задаче. Отсюда также следует, что получаемые результаты позволяют определить чувствительность критерия к изменениям X.

4. Метод ДП не накладывает каких-либо специальных требований на вид и форму представления функций, составляющих критерий. Так, в рассмотренной задаче функции r (V) могут быть недифференцируемыми, могут быть заданы даже в виде таблицы или графика, или задаваться алгоритмически.

5. Отыскание глобального экстремума многомерной функции является очень сложной проблемой. Динамическое программирование снижает размерность решаемых задач в N раз (по числу переменных), что значительно облегчает нахождение глобального экстремума. Так в рассмотренной задаче на каждом шаге находится максимум функции одной переменной. Из свойства рекуррентного соотношения следует, что отыскание глобального оптимума на каждом шаге гарантирует достижение глобального оптимума исходной задачи.

6. Наложение специфических условий на переменные не «утяжеляет» решение задачи методом ДП (в отличие от многих других). Например, ограничения сверху и снизу или/и дискретность (в частности, целочисленность) переменных не затрудняют, а, наоборот, облегчают решение на каждом шаге.

7. Трудоемкость вычислений и объем памяти для хранения результатов на одном шаге не зависят от числа шагов. Поэтому увеличение числа шагов приводит только к пропорциональному возрастанию времени решения задачи, тогда как для других методов с увеличением размерности задачи трудоемкость ее решения растет гораздо быстрее.

Для лучшего усвоения материала решение следующих двух задач поясняется на численных примерах.