
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод проектирования градиентаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Градиент дает направление, в котором функция возрастает с наибольшей скоростью. Однако при условной оптимизации оно, как правило, не является возможным направлением. Поэтому используют не сам градиент (антиградиент), а его проекцию на поверхность ограничений, точнее, на плоскость, аппроксимирующую эту поверхность в текущей точке. Очевидно, что проекция градиента определяет направление наискорейшего изменения функции на поверхности ограничений. Приведем один из вариантов метода проектирования градиента сначала для задачи с ограничениями-равенствами, а затем для общего случая. Метод применим, если целевая функция и все функции ограничений дифференцируемы. Пусть ограничения заданы в виде
Найдем возможное направление l, на котором скорость изменения целевой функции максимальна:
В допустимой области D функции yj постоянны. Поэтому искомое направление должно удовлетворять системе равенств
Из связи направления с координатами следует:
что перепишем в виде
Таким образом, для нахождения наилучшего возможного направления необходимо решить задачу оптимизации (8.56) – (8.58). Так как условия имеют вид равенств, а функции дифференцируемы, для решения этой вспомогательной задачи воспользуемся методом Лагранжа. Запишем функцию Лагранжа:
Неизвестными в ней являются векторы
Отсюда выразим компоненты искомого вектора:
Подставив (8.60) в (8.58), находим:
С учетом этого выражения формула (8.60) принимает вид
Для определения неизвестных множителей lj воспользуемся системой (8.57). Подставив в нее (8.61), получаем:
После раскрытия скобок окончательно имеем:
Так как направление ищется в конкретной точке, то все производные в (8.62) – известные константы. Поэтому система уравнений (8.62) является линейной системой относительно lj. Ее решение не вызывает затруднений (при условии, что матрица системы не является особенной). Найдя значения lj и подставив их в (8.61), получаем компоненты проекции градиента (в знаменателе (8.61) имеем длину проекции градиента). Движение осуществляется в направлении, противоположном проекции. Аналогично градиентному методу новая точка вычисляется по формуле
Алгоритм. 1. Задать начальную точку, удовлетворяющую системе (8.55), начальное значение h0 и точность по величине проекции градиента e. 2. В текущей точке вычислить градиенты всех функций (f и yj) и решить систему (8.62). 3. Вычислить проекцию градиента по формуле (8.61). 4. Проверить: если 5. Вычислить новую точку по формуле (8.63). 6. Проверить: если значение целевой функции улучшилось, перейти на шаг 2, иначе уменьшить hk в два раза и перейти на шаг 5.▲
При линейных ограничениях могут возникать проблемы поиска лишь при очень малых значениях градиентов функций ограничений и совпадении их направлений, так как это приводит к вырожденности матрицы системы (8.62). В случае нелинейных ограничений движение на основе линейной аппроксимации нарушает равенства. Поэтому в алгоритм необходимо внести изменения, обеспечивающие выполнение равенств с необходимой точностью ey. С этой целью алгоритм дополняется проверкой величины невязки, которая выполняется в каждой новой точке. Если
Для решения задачи (8.64) можно применить любой метод безусловной оптимизации, но в данном контексте целесообразен метод градиентов. При этом значения (n - m) переменных фиксируются, так как для выполнения равенств достаточно m переменных. Понятно, что при частых коррекциях трудоемкость алгоритма значительно возрастает. Теперь рассмотрим случай, когда ограничения заданы в виде неравенств jj (x)£0. Поиск начинается из точки, в которой удовлетворяются все ограничения. Пока они выполняются как строгие, движение осуществляется по градиентному методу. Когда достигается граница допустимого множества, одно или несколько ограничений обращаются в равенства. Такие ограничения называют активными. В точках с активными ограничениями направление движения определяется по проекции градиента на поверхность этих ограничений, то есть применяется вышеприведенный алгоритм. Пример поиска минимума при двух линейных неравенствах показан на рис. 8.40. Очевидно, что при смешанных и нелинейных ограничениях алгоритм весьма существенно усложняется и требует большого объема вычислений. Поэтому метод проектирования градиентов целесообразно применять при линейных ограничениях.
По своей концепции генетические алгоритмы близки к методам случайного поиска. В них сочетаются элементы случайности и детерминированности, что характерно для всех природных процессов. Заимствованием механизмов живой природы и обусловлено название "генетические". Идея генетических алгоритмов была высказана Д.Холландом в 60-е годы и затем развита им в фундаментальной работе "Адаптация в естественных и искусственных системах"(1975). Ипользовать их в численной оптимизации предложил Д.Гольдберг (1995). Но в основном генетические алгоритмы находят применение для обучения нейронных сетей. Поэтому здесь они будут рассмотрены только на уровне идей. Как уже отмечалось, генетические алгоритмы строятся по принципам функционирования живой природы. Детерминированная составляющая алгоритмов в большей степени представлена в моделировании процессов отбора, размножения и наследования, а случайная – процесса мутации. Любая альтернатива (вариант) представляется в виде строки (как правило, битовой) фиксированной длины, с которой манипулируют вне связи с содержанием задачи. Строка как абстрактная модель называется кодом. В коде в общем случае представлен набор параметров, зависящих от аргументов целевой функции. Код и его структура определяют генотип. Применительно к задачам оптимизации экземпляры кода, называемые хромосомами или особями, есть точки в пространстве поиска. Совокупность особей образует популяцию, а последовательные популяции – поколения. Основными параметрами конкретного алгоритма являются размер популяции и вероятности применения операторов. Первоначально по содержанию задачи формируется генотип и создается исходная популяция. Размер популяции N рекомендуется брать исходя из оценки числа возможных альтернатив r:
К текущей популяции применяется оператор отбора, в результате чего образуется множество родительских пар. При максимизации целевой функции вероятность особи стать родителем может вычисляться, например, по очевидной формуле
где fi – значение критерия на i- й особи. Для создания потомков используется оператор скрещивания, моделирующий процесс наследования за счет передачи части свойств от родителей к потомкам. Вероятность его применения рекомендуется брать не ниже 0,9. Он производит обмен подстроками родительских особей и, следовательно, от пары родителей образуется два потомка. Как это происходит, зависит от выбранной процедуры скрещивания. Например, при длине строки n из первых n- 1 равновероятных натуральных чисел разыгрывается одно число, которое принимается за точку разбиения. Затем подстроки родителей, находящиеся справа от точки разбиения, меняются местами. К новым особям применяется оператор мутации. Вместе с оператором скрещивания он позволяет расширить область поиска, получить особи со свойствами, отсутствующими у родителей. Вероятность мутации берется обычно не выше 0,01. Процесс мутации заключается в случайной перестановке двух элементов строки, в смене значения случайно взятого элемента строки с 0 на 1 или наоборот, в циклическом сдвиге элементов строки и т.п. Добавление потомков приводит к расширению популяции. В алгоритмах стационарного состояния все поколения имеют одинаковый размер. Поэтому на следующем шаге алгоритма производится сокращение популяции оператором редукции. Вероятность его применения к особи можно определить через вероятность отбора pi:
На последнем шаге цикла проверяется условие останова. В качестве критерия останова используют число поколений, качество поколения (пороговое значение), близость особей между собой и др. Для повышения эффективности генетических алгоритмов предлагаются способы распараллеливания вычислений, сокращения размера популяции за счет выделения кластеров и замены каждого одной особью, разрабатываются алгоритмы с изменяемым размером популяции. Отличительной чертой генетических алгоритмов является одновременное использование набора точек в пространстве поиска вместо перехода от точки к точке в традиционных методах. Эта особенность позволяет применять такие алгоритмы для решения многоэкстремальных задач. В заключение приведем небольшой пример, иллюстрирующий одну итерацию алгоритма. Пример 8.7. Найти целочисленный максимум функции f (x 1, x 2)=675- x 12- x 22+20 x 1+10 x 2 на области 5£ x 1£36, 2£ x 2£17. Сначала сделаем преобразования: x 1= y 1+5, x 2= y 2+2, тогда 0£ y 1£31, 0£ y 2£15. В этом случае новые аргументы функции y 1, y 2 можно представить в двоичной системе, а за код принять строку из 9 бит. Первые 5 бит будут отражать y 1, остальные – y 2. Определим размер популяции: N =2log2(16*32)=18. Ограничимся N =10. Используя датчик случайных чисел, создаем исходную популяцию и для всех ее особей вычисляем значение f и вероятность отбора pi (табл. 8.1). Таблица 8.1
Действия оператора отбора, использующего распределение pi, привели к выбору родительских пар (2,7), (5,10), (6,9), (1,4), (4,9). В каждой паре точки разбиения выбираются независимо с помощью датчика целых случайных чисел от 1 до 8 с равными вероятностями. Результаты работы оператора скрещивания приведены в табл. 8.2. Точки разбиения показаны косой чертой. Значения аргументов и функции даны для потомков.
Таблица 8.2
Теперь предположим, что оператор мутации сработал для 7 потомка, поменяв местами биты 1 и 2. Код этого потомка сменился с 011101110 на 101011010, значение функции стало 495. Расширенная популяция включает 10 исходных особей и 10 потомков. Сокращаем популяцию до принятого размера, отбрасывая особи с меньшими значениями функции. Полученная после этого популяция первого поколения представлена в табл. 8.3. В ней только первые 4 особи из исходной популяции. Таблица 8.3
Из сравнения данных в таблицах 8.1 и 8.3 видно, что новая популяция лучше исходной. Если среднее значение целевой функции на начальной популяции было равно 585,3, то на новом поколении оно возросло до 725,6. Следующий шаг заключается в проверке условия окончания поиска. Оно может быть представлено в разных вариантах: min fi > f min или max fi -min fi < ef, или n ³ n задан. В первом варианте все особи должны быть лучше заданного уровня качества, во втором критерием выступает близость особей, в третьем – число поколений (итераций). Если предположить, что выбранное условие выполняется на первом поколении, то поиск на этом заканчивается. За решение принимаем лучший результат: x 1=11, x 2=10, f =774. Оптимальному решению соответствуют значения: x 1=10, x 2=5, f =800. Сравнение показывает, что по значению критерия получено неплохое приближение к оптимуму. Понятно, что продолжение итераций приведет к дальнейшему улучшению популяции и получению более близкого к оптимальному решения.▲ Из описанной схемы генетического алгоритма и приведенного примера можно сделать вывод, что самым важным этапом применения алгоритма является определение генотипа (структуры кода) и для каждой задачи он индивидуален. Кроме того, специфика задачи может диктовать и требования к работе операторов. Например, в задаче коммивояжера оператор скрещивания не должен порождать потомков, в коде которых один пункт представлен более одного раза. Таким образом, по своей сути генетические алгоритмы являются эвристическими.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 757; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

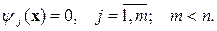 (8.55)
(8.55) (8.56)
(8.56) (8.57)
(8.57)
 (8.58)
(8.58) . (8.59)
. (8.59) и L. Взяв производные
и L. Взяв производные  и приравняв их нулю, получаем
и приравняв их нулю, получаем
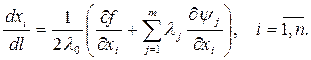 (8.60)
(8.60)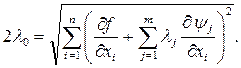
 (8.61)
(8.61)
 (8.62)
(8.62) . (8.63)
. (8.63) завершить поиск.
завершить поиск. Качественный характер работы алгоритма иллюстрирует рис. 8.39. Здесь функции зависят от 2-х переменных, поэтому в каждой точке на линии ограничения может быть всего 2 направления, лучшее из которых определяет проекция градиента. В многомерной задаче таких направлений бесконечное множество.
Качественный характер работы алгоритма иллюстрирует рис. 8.39. Здесь функции зависят от 2-х переменных, поэтому в каждой точке на линии ограничения может быть всего 2 направления, лучшее из которых определяет проекция градиента. В многомерной задаче таких направлений бесконечное множество. , то включается процедура коррекции, заключающаяся в минимизации невязки:
, то включается процедура коррекции, заключающаяся в минимизации невязки: (8.64)
(8.64)

 (8.54)
(8.54)




