Метод наискорейшего спуска (метод Коши).

Величина шага выбирается из использования максимизации или минимизации целевой функции при движении в направлении градиента.

Используется информация о неведении первых производных.

Отсюда малая сходимость метода.

Метод Ньютона.

Производится квадратическая аппроксимация целевой функции, что позволяет использовать информацию о поведении вторых производных. Это позволяет менять шаг в зависимости от расстояния до оптимума. Увеличивается шаг, где градиент меняется медленно и наоборот.

Достоинства:

1) Лучшая сходимость относительно первой производной чем у метода градиента;

2) Не нужно знать аналитические значения производных, а только их численные значения.

Недостаток: Нужно 2 раза дифференцировать.

 

Поисковые методы

Безградиентные методы.

1) Используются для поиска экстремума в унимодальных функциях.

2) Не надо искать производные, нужно лишь знать значения целевой функции в определенных точках.

3) Все методы многошаговые (итерационные).

4) Они имеют разную сходимость.

К ним относятся:

· Методы общего поиска,

· Метод дихотомии.

· Метод золотого сечения.

· Метод чисел Фибоначчи

Метод общего поиска

а) Метод покоординатного поиска (метод Гаусса-Зейделя).

Все переменные, кроме одной, фиксируются, а одна, нефиксированная – изменяется, пока не достигнет наилучшего результата целевой функции (max или min), затем она фиксируется и идет переборка остальных переменных по одной.

Недостатки:

1) малая сходимость из-за большого числа шагов;

2) слабо используется информация, полученная на предыдущем шаге;

3) малая точность метода при одинаковом шаге.

Достоинства:

1) Целевая функция может зависеть от нескольких переменных.

 

б) Покоординатный поиск с циклическим изменением координат.

Все переменные, кроме одной фиксируются, а одна изменяется следующим образом: делается один шаг в одну сторону и два шага в обратную. Во всех трех точках вычисляется значения целевой функции, из них выбирается наилучшее (точка, которая наиболее близка к оптимуму).

Достоинства:

1) Сходимость немного лучше.

Недостатки:

1) Те же.

 

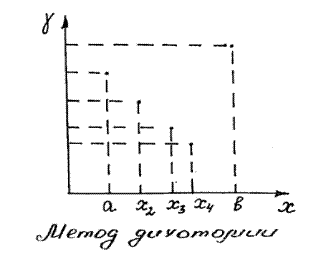
в) Метод комбинированный.

Вначале используется покоординатный поиск, а вблизи экстремума используется метод б) с переменным шагом.

Достоинства:

1) Сходимость и точность стали лучше.

2. Метод дихотомии

Метод работает для одной переменной

Отрезок ООФ делится пополам и одна из половинок снова делится пополам. Вычисляется значение в четырех точках. Сравниваются значения целевой функции и неудовлетворяющие значения отбрасываются.

Достоинства:

1) простота.

Недостатки:

2) небольшая сходимость;

3) ситуации неопределенности отбрасывании отрезка, когда одно значение равно другому;

4) исследуется функция, только от одной переменной.

 

 

Метод почти половинного деления.

Отрезок делится пополам от середины берутся еще 2 точки на одинаковом удалении x. Отбрасывается участок без минимума.

Достоинства:

1) простота;

2) используется информация, полученная на предыдущем шаге;

3) лучшая сходимость.

 

Метод золотого сечения.

 

- Формула золотого сечения

Приравниваем z=1

Составляем квадратичное уравнение z₂²=z₁ = z-z₂=(1-z₁)²

z₂²+ z₂-1=0

z₁»0.382

x₂»0.618

 

 

 

Тогда отрезок делится в этом соотношении. Вычисляется значение g функции, затем отбрасывается часть без минимума.

 

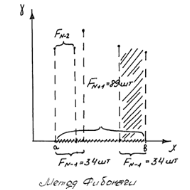
Метод чисел Фибоначчи.

Ряд чисел Фибоначчи:

- арифметическая прогрессия

Введем понятие интервала неопределенности, в котором находится экстремум после выполнения операции исключения отрезков.

Обычно .

Алгоритм работы метода Фибоначчи:

1) Зная интервал поиска (Параметры а и b) находим число Фибоначчи по соотношению:

2) По числу f находится из ряда ближайшее большее число F.

Пример: f = 38, = 55 => n = 10.

3) Интервал поиска делим на количество отрезков F_n+1. (Если 55, то делим на 89)

 

4) С двух сторон от а и b откладываем количество отрезков F_n+1.

5) Вычисляем значения g в 4-х точках, ищем g_max

6) Далее все пункты повторяются

Полученный интервал будет удовлетворять условию обеспечения точности.

 

Достоинства:

1) эффективен;

2) эффективно используется информация, полученная на предыдущем шаге, за счет лучшего выбора точек.