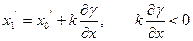Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы оптимизации, основанные на классической математике.Содержание книги
Поиск на нашем сайте
1. Экстремум функции одной переменной
2. Экстремум функции многих переменных
Исследуем матрицу: Если все элементы матрицы больше 0, то в точке наблюдается минимум. 3. Метод замены переменных Когда ограничения имеют вид неравенств, число ограничений меньше числа переменных (неизвестных).
Выражаем m первых переменных:
Выражаем через остальные. Получаем систему уравнений.
Затем уже находятся все остальные переменные подствавлением в эти.
Достоинства: 1) позволяет избавиться от ограничений; 2) позволяет понизить размерность задачи. Недостатки: 1) не всегда можно разрешить систему уравнений, относительно m - первых неизвестных (переменных). 2) Необходимо, чтобы функция была дифференцируема. 4. Метод неопределенных множителей Лагранжа. Достоинства: 1) Нет ограничения на условие, что количество переменных Задача с ограничениями сводится к задаче без ограничений. Составляется ф-я Лагранжа: где Находим производные:
Находим производные по каждой из
Решаем (1) и (2) и находим: (1) =› (2) =› т.о. уходим от ограничений. Недостатки: 1) функция должна быть дифференцируема; 2) трудность решения систем уравнений; 3) повышена размерность задачи.
Пример: Спроектировать термостат цилиндрической формы, т.о., чтобы он имел min поверхность при заданном объеме. r, h -?
Нелинейное программирование
Особенности задач нелинейного программирования: 1) Многошаговые интеграционные процессы, в которых производится постепенное сведение к оптимальному решению. Точки друг от друга различаются на шаг.
где 2) Большую трудность вызывает выбор шага (если большой – рискуем пройти оптимум, но с большой скоростью; если маленький – существует возможность «утонуть» в вычислениях). 3) Заранее определить число шагов нельзя. 4) Эффективность методов зависит от результата, полученного в предыдущем шаге. 5) В алгоритме поиска необходимо иметь правило окончания работы. Оно заключается в достижении требуемой точности. 6) Некоторые задачи могут не иметь решения, а иметь лишь особые точки.
Классификация методов нелинейного программирования:
- метод градиента и его модификаций; - метод релаксации; - метод наискорейшего спуска; - метод тяжелого шарика;
- метод общего поиска; - метод дихотомии; - метод золотого сечения; - метод чисел Фибоначчи; - метод сканирования; - симплексный метод;
- метод «слепого» поиска; - метод случайных направлений. Градиентные методы нелинейного программирования. Метод релаксации. Применяется в задачах, где трудно или невозможно отыскать оптимум в аналитической форме. Исходная задача разбивается на ряд подзадач.
В области определения выбирается точка
Все переменные оставляем const, а xосвобождаем
Находим производную:
Значение подставляется в функцию
Дальше таким же образом берется производная и находится:
т. е. за
Сравнивая После сравнения выбираются максимальное и минимальное значение функции, которые и дают наиболее оптимальные значения
Достоинства: 1) Простота и наглядность. Недостатки: 2) Долгий путь решения задачи. 3) Необходимо иметь аналитические выражения целевой функции по всем параметрам. Метод градиента. Исключает недостатки предыдущего метода и использует основное свойство градиента: вектор градиента всегда направлен в сторону наибольшего изменения функции. Требование: Функция должна быть дифференцируема, унимодальная (иметь 1 экстремум) на определенном промежутке.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.158.111 (0.009 с.) |

 =>Находится Xопт
=>Находится Xопт
 => Находится Xопт
=> Находится Xопт - матрица вторых производных.
- матрица вторых производных.

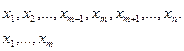

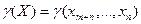 - целевая функция зависит от меньшего числа переменных
- целевая функция зависит от меньшего числа переменных
 ,
, - неопределенные множители Лагранжа.
- неопределенные множители Лагранжа. (1)
(1) :
: (2)
(2)
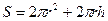


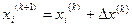 ,
, шаг, k - номер интеграции, номер шага.
шаг, k - номер интеграции, номер шага.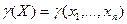
 и составляется функция вида:
и составляется функция вида:

 =0 => x1(1)=const
=0 => x1(1)=const :
: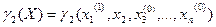
 и т.д.
и т.д.
 шагов вычисляем
шагов вычисляем  , производим сравнение
, производим сравнение  и
и 


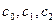 ,…, выбирают max и min значения.
,…, выбирают max и min значения. – оптимальное значение.
– оптимальное значение.