
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура конструкции эва и их математические модели.Содержание книги
Поиск на нашем сайте
Структура – схема устойчивых однородных связей между элементами конструкции, т. е. множество, состоящее из подмножеств
Каждое из этих подмножеств – структура. Эти структуры классифицируются по природе связей.
Структурная схема – условное графическое изображение элементов конструкции и связей между ними Для описания используется математическая логика и теория графов.
Пример 1:
Пример 2: 1-2 Путь (Однозвеньевой)
Математические модели структурных схем, служат для анализа путей в графе, нахождения кратчайших путей, отыскания изолированных вершин и нахождения избыточных путей и т.д. Путь в графе – последовательность ребер, в которой конец каждого предыдущего ребра совпадает с началом последующего ребра. Ребра, входящие в путь называются звеньями. Существуют пути:
Математической моделью структурной схемы является матрица непосредственных путей (матрица инценденции).
Алгоритм составлении матрицы: 1) Вершины графов номеруются в произвольном порядке. Порядок графа равен числу вершин в графе. 2) Строки и столбцы матрицы номеруются теми же номерами, что и вершины в графе. Элемент матрицы Элемент равен 0 в противоположном случае (если количество путей больше 1, то ставиться количество путей)
Ранг элемента структурной схемы – (показатель качества структурной схемы) численно равен суммарному значению однозвенных, двухзвенных и т. д. путей, связывающих данную вершину с другими вершинами структурной схемы
где
Пример:
Однозвенная:
Двухзвенная:
Т.о. первая вершина самая нагруженная (У нее максимальный ранг и из нее выходит наибольшее количество путей)
Параметры конструкции ЭВА и отклонение параметров.
Параметры – величины, которые численно характеризуют свойства конструкции
Отклонение параметров называется мерой несоответствия его действительному (номинальному) значению.
Относительное отклонение параметров:
Отклонение параметров можно разбить на:
Допуск на параметр – полученное расчетом или в результате экспериментов отклонение параметра, при котором прибор может выполнять свои функции с заданной точностью в пределах установленного времени и в условиях влияния окружающей среды. Методы анализа отклонения параметра Отклонение параметров ведет к снижению точности, стойкости, надежности. С другой стороны, уровень отклонения параметров определяет стоимость прибора. Анализ заключается в определении величин отклонения параметров элементов и самого аппарата. Методы делятся на: 1) статистические, 2) корреляционные, 3) расчетно-аналитические.
Достоинства статистического и корреляционного методов: 1) дают точный результат, Недостатки статистического и корреляционного методов: 1) трудоемкость, 2) нельзя использовать при разработке новой техники. Расчетно-аналитические методы основаны на выявлении экспериментальным путем зависимости между отклонениями исследуемого параметра и отклонениями других параметров, от которых зависят исследования.
Пример: Прямая задача
Обратная задача
Расчетно-аналитические методы делятся на: 1) метод предельных отклонений, 2) метод квадратического сложения, 3) вероятностный метод отклонения параметров. Метод предельных отклонений Основан на оценке наихудшего сочетания отклонения отдельных параметров. Преимущества: 1) достаточно прост Недостатки: 1) дает очень приближенные результаты. Завышение от двух до десяти раз за счет того, что рассматриваются предельные отклонения.
Разлагаем (2) в ряд Тейлора:
Из выражения (3) получаем:
Для выводов необходимо, чтобы функция была дифференцируема до Упрощая:
Таким образом получаем уравнение отклонения параметра для метода отклонения предельных параметров (МОПП):
Для перехода к относительным величинам делим все на
Уравнение отклонения параметра в форме относительных значений:
Для практического применения используют следующие соотношения: 1) 2) где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.78 (0.007 с.) |


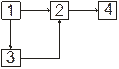
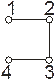 1-3-4 Путь (Двузвеньевой)
1-3-4 Путь (Двузвеньевой)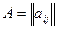 , принадлежащий
, принадлежащий  -ой строке
-ой строке 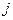 -му столбцу равен 1, если из вершины
-му столбцу равен 1, если из вершины  ,
, - ранг, для однозвенной матрицы (Для каждой вершины ранг свой)
- ранг, для однозвенной матрицы (Для каждой вершины ранг свой)




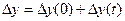 ,
, - производственное отклонение параметра (Постоянно во времени. Возможно управлять путем совершенствования технологического процесса.)
- производственное отклонение параметра (Постоянно во времени. Возможно управлять путем совершенствования технологического процесса.) - неустойчивость параметра во времени.
- неустойчивость параметра во времени.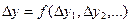
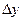 - отклонение исследуемого параметра,
- отклонение исследуемого параметра,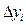 - отклонение независимых параметров.
- отклонение независимых параметров.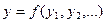


 (1)
(1)
 (2)
(2) (3)
(3) (4)
(4) порядка и отклонения
порядка и отклонения 


 :
:

 - коэффициент влияния. Показывает влияние
- коэффициент влияния. Показывает влияние 

 ,
, - константы.
- константы.


