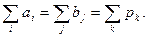Транспортная задача с ограниченными пропускными

способностями (T_d - задача)

Отличается от предыдущей задачи учетом ограничений на пропускные возможности коммуникаций. В реальных условиях пропускные способности дорог, воздушных коридоров, линий связи и т.п. всегда ограничены сверху. Если известно, что фактическая загрузка будет заведомо меньше, задача рассматривается как простейшая. В противном случае учет этих ограничений приводит к более сложной транспортной задаче, называемой Т_d-задачей. Ее модель имеет вид

(5.7)

(5.8)

(5.9)

0 £ X_ij £ d_ij, " i,j, (5.10)

где d_ij –пропускная способность коммуникации i j.

Ограничения (5.10) вносят существенные коррективы в свойства задачи. Из особенностей модели, присущих Т-задаче, сохраняются все, кроме последней. В Т_d-задаче условие сбалансированности не является достаточным для разрешимости задачи. Более того, в число необходимых условий существования решения помимо его входят еще две группы условий, отражающих физическую реализуемость решения:

(5.11)

(5.12)

Они требуют, чтобы суммарная пропускная способность коммуникаций, входящих в каждый ПН была не меньше объема поставок, а выходящих из ПО – не меньше количества вывози­мого груза. Если хотя бы одно из них нарушается, задача заведомо неразрешима.

Однако и выполнение всех необходимых условий не гарантирует разрешимость Т_d-задачи. Например, условия (5.1), (5.11) и (5.12) выполняются для транспортной сети, показанной на рис. 5.1, что легко проверить. Но задача неразрешима, так как невозможно поставить во второй пункт назначения 8 единиц груза.

Задачи с неоднородным грузом

В рассмотренных задачах по умолчанию предполагалось, что для отправителей и получателей грузы неразличимы – это задачи с однородным грузом. Если в перевозках участвуют несколько видов груза с одинаковыми или различными транспортными затратами, исходную многопродуктовую задачу можно разбить на задачи с однородным грузом (по числу видов).

Если же имеет место взаимозаменяемость грузов у получателей, то исходную задачу нельзя разделить на отдельные задачи. Например, получателю нужен каменный и бурый уголь. Известна потребность в том и другом и, кроме того, есть потребность, которая может быть удовлетворена любым из них. Последняя измеряется в единицах либо каменного, либо бурого угля. Такие задачи называют задачами с неоднородным грузом. В случае отсутствия ограничений на пропускные способности они легко преобразуются к задачам с однородным грузом.

Взаимозаменяемость грузов характеризуется коэффициентом взаимозаменяемости . Например, если 1 т. каменного угля заменяет потребителю 2 т. бурого, то Зная все грузы можно привести к одному виду. Затем вместо одного исходного ПО вводится столько, сколько в нем видов груза. Аналогично каждый исходный ПН заменяется новыми, число которых равно числу видов потребностей. Наконец, определяются приведенные затраты на перевозки между всеми новыми пунктами. Если виды грузов в ПО и ПН совпадают, затраты на перевозку равны исходным C_ij; если же они разные, то перевозка запрещается (C_ij = М). Между ПО с пересчитанным грузом и ПН с взаимозаменяемой потребностью затраты равны

После таких преобразований модель задачи записывается аналогично случаю с однородным грузом, а ее размерность определяется числом пунктов, заменяющих исходные.

Для разрешимости задачи необходимо кроме сбалансированности, чтобы по каждому виду груза суммарные возможности были не меньше суммарной потребности (без учета взаимозаменяемой). Однако и при выполнении всех необходимых условий возможна неразрешимость задачи из-за присутствия запрещенных перевозок.

Многоиндексные задачи

Для учета дополнительных условий перевозки вводятся переменные с числом индексов более двух. В таких случаях говорят о многоиндексных транспортных задачах. Например, если существенное значение имеет вид транспорта, то в модели используются переменные X_ijk, означающие количество груза, перевозимое из i -го пункта в j -й k -ым видом транспорта. Модель трехиндексной задачи зависит от конкретных условий. Если в исходных данных имеем производительность каждого вида транспорта p_k и не учитываются пропускные способности, то задача описывается трипланарной моделью:

Она идентична Т-задаче. Отличие лишь в числе переменных и групп условий. Поэтому каждая переменная входит в модель ровно три раза, а сбалансированность, как необходимое и достаточное условие разрешимости задачи, записывается в виде

Если транспортные средства принадлежат разным перевозчикам, то в модели будут фигурировать четырехиндексные переменные X_ijkl, где l – индекс перевозчика.

Дальнейшая детализация условий транспортировки может потребовать переменных с пятью и более индексами. В ряде случаев многоиндексные задачи удается свести к двухиндексным.