
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двойственная пара транспортных задачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Построим двойственную задачу простейшей транспортной задачи (Т-задачи). Предварительно изменим знаки в выражении критерия и в условиях по пунктам назначения. Тогда модель прямой задачи примет вид:
Здесь слева от равенств записаны сопоставленные им двойственные переменные. Модель двойственной задачи запишем по правилам, приведенным в разд. 4.11.3:
Если Cij перенести в левую часть, то согласно (5.19) условия двойственной задачи приобретают смысл признака оптимальности "Δij£0. Итак, если выполняются условия прямой и двойственной задач, решение оптимально. Теперь понятно, что потенциалы представляют собой переменные двойственной задачи. Из теорем двойственности известно, что в оптимальном решении критерии прямой и двойственной задач равны. Для рассматриваемой двойственной пары это означает, что
Отсюда находим:
Учитывая линейность (5.21), полный дифференциал запишем в виде
Изменения ai и bj могут быть только равными, иначе нарушится сбалансированность задачи. Если положить D ai= D bj =1, то получим
Следовательно, разность потенциалов показывает, как изменится оптимальное значение критерия при одновременном изменении соответствующих потребностей и возможностей на единицу. 25. Метод потенциалов для Td-задачи Транспортная задача с ограниченными пропускными способностями (5.7)-(5.10) отличается от T-задачи наличием ограничений сверху на перевозки: 0 £ xij £ dij. Они существенно усложняют решение задачи. В плане перевозок не все положительные переменные являются базисными. В невырожденном решении базисные переменные могут принимать только значения больше нуля и меньше пропускной способности: 0 < xij < dij. (5.24) В вырожденном решении некоторые базисные переменные равны граничным значениям (0 или dij). Если задача не сбалансирована, то, как и в Т-задаче, добавляют столбец или строку с нулевыми затратами, но с бесконечной пропускной способностью. Правило северо-западного угла непригодно для построения начального решения. Его строят по одному из вариантов правила минимального элемента. При этом принцип определения значений переменных сохраняется: на каждом шаге присваивается максимальное допустимое значение согласно формуле Xij =min(остаток от ai, остаток до bj, dij). Если минимум достигается на dij, то не закрывается ни строка, ни столбец, и следует продолжать движение по строке или столбцу (если двигались по столбцу). Однако может оказаться, что в строке (столбце) больше нет открытых клеток, а она не закрыта. Это значит, что начальный план получается недопустимым. Если часть строк (столбцов) не закрыта, то обязательно не закроются и некоторые столбцы (строки). Так как задача сбалансированная, то суммарная величина незакрытия строк После построения начального плана определяются базисные клетки по условию (5.24). Если таких клеток окажется меньше m+n-1 (вырожденный план), то в число базисных включают переменные (клетки), равные нулю или dij. При этом на базисных клетках не должен строиться замкнутый цикл, иначе клетки добавлены неверно. Пример 5.4. Исходные данные задачи приведены в табл. 5.6. В клетках слева даны пропускные способности (красным цветом), справа – затраты на перевозки (синим цветом). Задача сбалансированная. Начальный план строим по правилу минимального элемента, порядок построения показан стрелками (табл. 5.7). Строка 4 и столбцы 2 и 3 не закрылись: g =3.
Таблица 5.6 Таблица 5.7
Поэтому добавляем фиктивные строку и столбец, и в клетки незакрытых столбцов и строки записываем недостающие перевозки. В результате выполняется баланс по всем строкам и столбцам. Построенный искусственный (недопустимый) начальный план приведен в табл. 5.8 Так как общее число пунктов равно 9, то базисных переменных должно быть 8. Из сравнения значений xij и dij находим только 7 базисных переменных (базисные клетки закрашены), то есть план вырожденный. В качестве недостающей базисной клетки возьмем клетку 4,2 (закрашена более темным цветом), в которой значение переменной находится на верхней границе. Нетрудно убедиться, что ни из каких базисных клеток нельзя построить замкнутый цикл. (Чтобы соблюдалось это требование в случае вырожденности плана, можно рекомендовать рассматривать в качестве кандидатов на включение в число базисных в первую очередь те клетки, в которых происходит поворот на 90 градусов при построении плана. Так, в данном примере такими являются клетки 4,2 и 4,3.) ▲ Таблица 5.8
Если условия не выполняются хотя бы для одной небазисной клетки, решение может быть улучшено. В связи с этим введем два множества: - множество индексов переменных на нижней границе
- множество индексов переменных на верхней границе
Очевидно, что объединенное множество G=
Так как переменная вводится по-разному, увеличивается с нижней границы и уменьшается с верхней, вычисление q0 и перемещение по циклу выполняется иначе, чем в Т-задаче. При определении q0 теперь необходимо учитывать обе границы: при вычитании нельзя вычесть больше, чем имеется, а при добавлении недопустимо превысить пропускную способность. Из (5.26) следует, что возможны 2 варианта при выборе вводимой переменной и соответственно 2 варианта перехода к новому плану: 1. Если
2. Если
В обоих вариантах значение критерия улучшается на величину q0 |Dkr|. Таким образом, алгоритм решения сбалансированной Тd-задачи включает следующие шаги: 1. Построение начального плана перевозок. План может получиться как допустимый, так и искусственный (недопустимый). 2. Выделение базисных клеток. Если их меньше m+n- 1, то добавляются клетки на границе. 3. Нахождение потенциалов из системы (5.18). 4. Вычисление оценок по формуле (5.19) 5. Начало цикла. Определение множества G по матрицам плана и оценок. 6. Проверка признака оптимальности: если G =Æ (эквивалент (5.25)), переход на шаг 10. 7. Определение вводимой переменной (клетки kr) по (5.26) и построение цикла пересчета. 8. Построение нового плана: вычисление q0 в зависимости от принадлежности kr по (5.27) или (5.28) и соответствующее перемещение по циклу. 9. Получение матрицы оценок нового плана с помощью преобразования матрицы оценок старого плана (как в Т-задаче). Переход на шаг 5. 10. Конец. Полученный план является оптимальным, если не содержит запрещенных перевозок (с затратами М). Когда решение начинается с искусственного плана, то после достижения допустимого решения можно сократить матрицы перевозок и оценок за счет отбрасывания фиктивных столбца и строки. Если в них было ровно две базисные клетки, то пересчитывать матрицу оценок не надо. Иначе она рассчитывается через потенциалы для сокращенного плана. Однако сокращение матриц не является обязательным.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 531; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

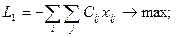

 ;
;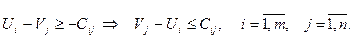
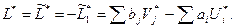 (5.21)
(5.21)


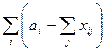 будет равна суммарному незакрытию столбцов
будет равна суммарному незакрытию столбцов  . Обозначим эту величину g. Чтобы в этом случае завершить построение начального плана, добавляют фиктивного потребителя (столбец) и фиктивного поставщика (строку) с одинаковой потребностью и возможностью g. Так как их клетки соответствуют искусственным переменным, которые в разрешимой задаче должны стать равными нулю, затраты в них полагают бесконечно большими (М), а в клетке на пересечении фиктивного столбца с фиктивной строкой – равными нулю. Пропускные способности в фиктивных клетках не лимитируются. В процессе работы алгоритма план станет допустимым, когда все искусственные переменные обнулятся, то есть в юго-восточной клетке перевозка станет равна g (фиктивный поставщик замкнется на фиктивного потребителя).
. Обозначим эту величину g. Чтобы в этом случае завершить построение начального плана, добавляют фиктивного потребителя (столбец) и фиктивного поставщика (строку) с одинаковой потребностью и возможностью g. Так как их клетки соответствуют искусственным переменным, которые в разрешимой задаче должны стать равными нулю, затраты в них полагают бесконечно большими (М), а в клетке на пересечении фиктивного столбца с фиктивной строкой – равными нулю. Пропускные способности в фиктивных клетках не лимитируются. В процессе работы алгоритма план станет допустимым, когда все искусственные переменные обнулятся, то есть в юго-восточной клетке перевозка станет равна g (фиктивный поставщик замкнется на фиктивного потребителя). 12
12
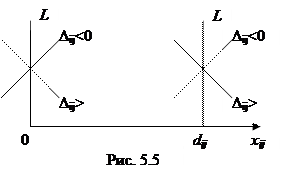 Теперь рассмотрим изменения на основном этапе алгоритма. Признак оптимальности в Td-задаче расширяется. Согласно (5.15) при введении в решение небазисной переменной xij= 0, то есть ее увеличении, критерий уменьшается при D ij >0 и увеличивается при D ij <0. Если же вводить переменную xij=dij, а это означает ее уменьшение, то критерий уменьшится при D ij <0 и возрастет при D ij >0. Этот характер изменения критерия показан на рис. 5.5. Поэтому решение не может быть улучшено, если выполняются условия, составляющие признак оптимальности задачи с ограниченными пропускными способностями:
Теперь рассмотрим изменения на основном этапе алгоритма. Признак оптимальности в Td-задаче расширяется. Согласно (5.15) при введении в решение небазисной переменной xij= 0, то есть ее увеличении, критерий уменьшается при D ij >0 и увеличивается при D ij <0. Если же вводить переменную xij=dij, а это означает ее уменьшение, то критерий уменьшится при D ij <0 и возрастет при D ij >0. Этот характер изменения критерия показан на рис. 5.5. Поэтому решение не может быть улучшено, если выполняются условия, составляющие признак оптимальности задачи с ограниченными пропускными способностями: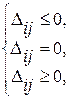
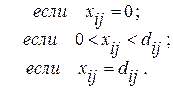 (5.25)
(5.25) ;
;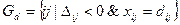 .
.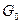 È
È 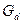 является множеством индексов перспективных переменных (клеток): введение любой из них приведет к улучшению критерия. В Т-задаче имеется только множество
является множеством индексов перспективных переменных (клеток): введение любой из них приведет к улучшению критерия. В Т-задаче имеется только множество  (5.26)
(5.26)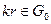 , то цикл строится на клетке, в которой перевозка равна нулю. Новый план получается прибавлением q0 в четных вершинах цикла и вычитанием в нечетных. Поэтому
, то цикл строится на клетке, в которой перевозка равна нулю. Новый план получается прибавлением q0 в четных вершинах цикла и вычитанием в нечетных. Поэтому . (5.27)
. (5.27)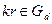 , цикл строится на клетке, в которой перевозка равна dij. В этом случае вводимая переменная должна уменьшаться. Поэтому перемещение по циклу состоит в вычитании q0 в четных вершинах и прибавлении в нечетных. Отсюда следует, что
, цикл строится на клетке, в которой перевозка равна dij. В этом случае вводимая переменная должна уменьшаться. Поэтому перемещение по циклу состоит в вычитании q0 в четных вершинах и прибавлении в нечетных. Отсюда следует, что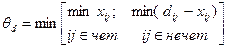 . (5.28)
. (5.28)


