
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрирование вектора ограничениийСодержание книги
Поиск на нашем сайте Пусть оптимальное решение X* получено для вектора Рассмотрим только случай линейной зависимости B (l)= B + l V, (4.41) где l³0 – параметр, определяющий величину изменения вектора ограничений; V – вектор размерности m, определяющий направление и относительную скорость изменения компонентов вектора ограничений. Этот вектор задается ЛПР исходя из прогноза возможных изменений ресурсов. Например, для трехмерного вектора B изменения могут быть заданы в виде
то есть ожидается одновременное уменьшение первого и третьего ресурсов и увеличение второго ресурса. При этом абсолютная величина изменения первого ресурса в три раза, а второго в полтора раза больше, чем третьего. Для любого базисного решения условия задачи AX = B можно записать в виде A B X B+ A H X H= B, где индексы “B” и “H” обозначают базисные и небазисные векторы (матрицы). Так как небазисные переменные равны нулю, то отсюда следует A B X B= В и, в частности, для оптимального решения A *B X *B= В. (4.42) Так как мы исходим из наличия решения X *, то базисная матрица
Очевидно, что если заменить в (4.42) B на B (l) при l =0, то ничего не изменится. При невырожденном оптимальном решении малое изменение B (l >0 мало ) не изменяет базис: оптимальная вершина хотя и смещается, но образуется теми же ограничениями. Поэтому в данном случае изменяется только оптимальное решение. Оптимальное решение при l >0 обозначим X**. Тогда для малых l равенство (4.42) запишется в виде
откуда находим изменяемое оптимальное решение
С учетом (4.43) окончательно имеем
где
Таким образом, при линейном характере изменений ресурсов оптимальные значения переменных также меняются линейно. Однако это справедливо до тех пор, пока не происходит смена базиса. В невырожденном решении всегда найдется l >0, при котором базис не меняется. Из выражения (4.44) следует, что при неотрицательном векторе P возрастание l не может привести к уменьшению какой-либо базисной переменной и, значит, к смене базиса. В этом случае формула (4.44) справедлива для любых l >0. Такая ситуация показана на рис. 4.12, где изменение b 1и b 2в направлении стрелок не приводит к смене базиса (вершины, в которой достигается оптимальное решение).
Значение l, при котором происходит смена базиса (базисного решения), называется критическим. Оно определяется по очевидной формуле
где pi – компоненты вектора Р. Таким образом, исходное решение можно использовать для определения изменяемых решений по формуле (4.44) только в диапазоне
Отсюда получаем максимальное изменение правой части
Пример 4.7. Параметрируем задачу, решенную симплекс-методом в разд. 4.9.7 (пример 4.2) в предположении изменения 1-го и 4-го ресурсов. Анализ поступления этих ресурсов показал, что первый может возрастать, а четвертый – уменьшаться, причем изменение четвертого может быть по абсолютной величине в два раза больше, чем первого. На этом основании записываем вектор изменений V =(1,0,0,-2). Взяв обратную матрицу из оптимальной симплекс-таблицы (в столбцах начального базиса), по формуле (4.45) вычисляем вектор P:
Выписываем исходное оптимальное решение, соблюдая порядок базисных переменных в последней таблице:
Из данного порядка следует, что первый компонент вектора P соответствует 6-й переменной, а последний – первой. Таким образом, параметрическое решение запишется в виде
Так как вектор P имеет отрицательные компоненты, вычисляем критическое значение l
Оно позволяет определить критические отклонения ресурсов от исходных значений:
Следовательно, полученное параметрическое решение будет спаведливо при одновременном изменении ресурсов в диапазонах 19 £ b 1 < 20,6; 13,8 < b4 £ 17. Чтобы расширить эти диапазоны, в задаче нужно заменить вектор B =(19; 13; 12;17) вектором B 1=(20,6;13;12;13,8) и снова решить ее. Новое решение параметрируется аналогичным образом. Замечания. 1) Вместо принятого в примере вектора V можно брать k V, где k – любое положительное число. При этом будет изменяться в k раз только
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 . Поставим вопрос: как будет изменяться оптимальное решение при изменении правой части, заданном параметрически B (l)?
. Поставим вопрос: как будет изменяться оптимальное решение при изменении правой части, заданном параметрически B (l)? ,
, - неособенная и существует обратная к ней матрица
- неособенная и существует обратная к ней матрица 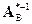 , умножая на которую слева равенство (4.42), получаем.
, умножая на которую слева равенство (4.42), получаем. . (4.43)
. (4.43)
 ,
,
 (4.44)
(4.44)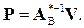 (4.45)
(4.45)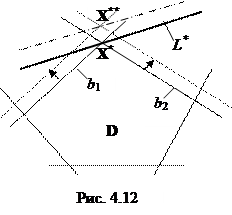 Если же среди компонент вектора Р есть отрицательные, то соответствующие базисные переменные с увеличением l
Если же среди компонент вектора Р есть отрицательные, то соответствующие базисные переменные с увеличением l 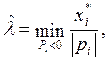 (4.46)
(4.46) .
.
 Если диапазон изменения правой части недостаточен, то для его расширения необходимо заново решить задачу с вектором B 1= B +Δ B max.Тогда получим новое оптимальное решение, новую обратную матрицу и на их основе снова проводится параметрирование для B (l)= B 1+ l 1 V. Повторяя эти действия, можно охватить весь желаемый диапазон изменения ресурсов. При этом соотношение компонент (но не знаков!) в векторе V может остаться исходным или измениться. В последнем случае зависимость от параметра l на всем исследованном диапазоне будет кусочно-линейной.
Если диапазон изменения правой части недостаточен, то для его расширения необходимо заново решить задачу с вектором B 1= B +Δ B max.Тогда получим новое оптимальное решение, новую обратную матрицу и на их основе снова проводится параметрирование для B (l)= B 1+ l 1 V. Повторяя эти действия, можно охватить весь желаемый диапазон изменения ресурсов. При этом соотношение компонент (но не знаков!) в векторе V может остаться исходным или измениться. В последнем случае зависимость от параметра l на всем исследованном диапазоне будет кусочно-линейной.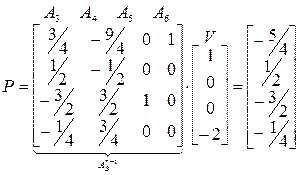




 а диапазоны изменения bi останутся прежними. 2) Очевидно, что если изменяется правая часть только в одном условии и в векторе V соответствующий компонент взят равным единице, то коэффициент при l в параметрической записи L** должен равняться двойственной переменной. При этом параметрический анализ позволяет определить диапазон изменения ресурса, в котором это значение двойственной переменной не меняется.
а диапазоны изменения bi останутся прежними. 2) Очевидно, что если изменяется правая часть только в одном условии и в векторе V соответствующий компонент взят равным единице, то коэффициент при l в параметрической записи L** должен равняться двойственной переменной. При этом параметрический анализ позволяет определить диапазон изменения ресурса, в котором это значение двойственной переменной не меняется.


