
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокритериальные задачи: функция полезности, лексикографический анализСодержание книги
Поиск на нашем сайте Как видно из предыдущих разделов, математические методы оптимизации позволяют находить эффективные решения. Однако из-за несравнимости эффективных решений не удаётся решить задачу со многими критериями до конца без привлечения ЛПР. Исходя из своих представлений об оптимальности решения ЛПР в конечном итоге отдаёт предпочтение одной из множества возможных альтернатив. В специальной литературе предложены различные способы вовлечения ЛПР в процесс принятия решений. В зависимости от того, на какой стадии процесса выявляются и используются предпочтения ЛПР, можно выделить три группы многокритериальных методов принятия решений: 1) основаны на том, что ЛПР может выразить свои предпочтения до начала процесса многокритериальной оптимизации; 2) интерактивные (диалоговые) методы; 3) методы построения множества эффективных решений с последующим представлением его ЛПР. В методах первой группы используются различные способы свёртки критериев, лексикографическое упорядочение критериев, установление желаемых уровней критериев и др. Вторая группа методов основана на непосредственном участии ЛПР в процессе оптимизации, когда на каждой итерации компьютер предлагает решения, а ЛПР их оценивает, и с учётом этих оценок компьютер ищет новые решения. Методы третьей группы отличаются друг от друга различными способами построения и представления множества эффективных решений. Прежде чем перейти к рассмотрению конкретных методов, сделаем одно замечание. На практике далеко не всегда принимаемое решение должно быть эффективным, так как оно соответствует (по определению) предельным возможностям системы. Например, желание иметь некоторые резервы может привести к выбору решения, которое не будет принадлежать множеству Парето. Однако и такой выбор должен основываться на знании эффективных решений с тем, чтобы правильно оценить границы возможного, а значит и сами резервы. Методы первой группы ЛПР может выразить свои предпочтения в различной форме. Это зависит от особенностей самого ЛПР, новизны задачи, типа и числа критериев и других факторов. Поэтому методы данной группы отличаются тем, что используют разные представления предпочтений и способы их формализации. Однако все они в конечном итоге сводят многокритериальную задачу к одной или ряду задач с одним (иногда обобщенным) критерием. Функция полезности В XIX веке экономисты высказали предположение о существовании у каждого индивидуума определённого количественного измерителя счастья или полезности – “пользометра”. Единицы измерения этого прибора назвали “утилями” (от английского utility – полезность). Согласно этой модели потребительского поведения каждый потребитель выбирает так товары и услуги, чтобы максимизировать свою полезность в пределах средств, которыми он располагает. Эта идея перенесена на многокритериальные задачи и интенсивно разрабатывается в теории полезности, ставшей самостоятельным направлением прикладной математики. Применительно к многокритериальной задаче в качестве товаров и услуг выступают критерии, а в качестве потребителя – ЛПР. При этом предполагается существование на множестве значений критериев y 1 ,y 2 ,….,ym скалярной оценки предпочтений ЛПР, называемой полезностью. Приведём строгое определение этого понятия. Функция U, которая каждой точке Y критериального пространства ставит в соответствие действительное число U (Y),называется функцией полезности (ценности) ЛПР, если
Y¢ ~ Y"Û U (Y')= U (Y"), Y'ýY"Û U (Y')> U (Y").
Таким образом, функция полезности представляет собой математическую модель предпочтений ЛПР. Если функция полезности известна, то многокритериальная задача сводится к стандартной задаче оптимизации: найти вектор X ÎD, максимизирующий U [Y(X)]. Множество точек критериального пространства, одинаковых по предпочтительности (для которых U (Y )= Const), образует гиперповерхность равного уровня функции полезности. Гиперповерхности равного уровня U (Y) называются кривыми безразличия, а семейство всех кривых безразличия – картой безразличия. Такая терминология связана с тем, что для любых двух альтернатив Y' и Y", лежащих на одной кривой безразличия, U (Y')= U (Y"), т.е. ЛПР всё равно, достигнет он Y ' или Y". Пример карты безразличия некоторой функции полезности и нахождение по ней оптимального решения показаны на рис. 10.4. Очевидно, что наибольшие затруднения при практическом применении рассматриваемого подхода вызывает построение функции полезности, адекватно отражающей предпочтения ЛПР.
 ), являются эквивалентными. Действительно, максимизация U 1(Y) и U 2(Y)= T [ U 1(Y)] приведет к одному результату, т.е. обе функции одинаково отражают структуру предпочтений ЛПР. ), являются эквивалентными. Действительно, максимизация U 1(Y) и U 2(Y)= T [ U 1(Y)] приведет к одному результату, т.е. обе функции одинаково отражают структуру предпочтений ЛПР.
В благоприятных случаях удается описывать предпочтения ЛПР функцией полезности, имеющей сравнительно простой вид: U(y 1 ,y 2 ,...,ym)=F [ U 1 (y 1 ),U 2 (y 2 ),...,Um(ym) ], (10.7) т.е. многомерная функция определяется через одномерные функции полезности значений одного отдельно взятого критерия. Типичные примеры таких функций для m =2: U (Y)= C 1 y 1 + С 2 у 2, С 1 >0, С 2 >0,
Формализация структуры предпочтений основана на Предельный коэффициент замещения критерия y 1 на критерий у 2 в точке ( Если коэффициент замещения не зависит от значений y 1 и у 2, то это означает, что кривые безразличия – прямые, имеющие вид y 1 + а предпочтения ЛПР могут быть представлены функцией U (Y )=y 1 + Если предельный коэффициент замещения зависит от значения у 2, но не зависит от y 1, то подходящей составной функцией полезности может быть U (Y )=y 1 + U 2 (y 2 ). (10.9)
Карта безразличия, соответствующая структуре предпочтений (10.9), имеет вид семейства кривых, которые получаются простым сдвигом по горизонтали (по оси у 1) одной из них. Аналогичный подход применяется и в случае, когда
Доказано, что структура предпочтений аддитивна и, следовательно, описывается функцией полезности вида U (Y )=U 1 (y 1 )+ U 2 (y 2 ) (10.10) тогда и только тогда, когда выполняется условие соответственных замещений. Одна из процедур построения функции (10.10), которую Для построения функции полезности предварительно устанавливаем область возможных значений критериев: U(y 1 ,y 2 )= где Ui(
В процедуре отыскания U в виде (10.11), приводимой ниже, одинаковость пар и значения средних точек определяет ЛПР в диалоге с аналитиком. I.Строим U 1 в следующей последовательности: -находим среднюю по полезности точку у -находим среднюю по полезности точку у -находим среднюю по полезности точку у -проверяем согласованность результатов: является ли у -по пяти определенным точкам (или большему числу, если продолжить дробление интервалов) строится график функции U 1 (y 1 ). 2. Таким же образом находим U 2 (у 2 ). 3. Определяем коэффициенты шкалирования U ( или
Значения U 1 и U 2 в точках Соответствие полученной функции полезности структуре предпочтений ЛПР можно дополнительно проверить, предложив ему несколько пар значений критериев (отличных от С увеличением размерности критериального пространства трудоемкость построения функции полезности даже в аддитивном виде резко возрастает. А при более сложной структуре предпочтений ЛПР отыскание адекватной U (Y)становится весьма проблематичным. Несмотря на то что имеется целый ряд хорошо разработанных процедур построения функции полезности (например, Р.Кини и Х.Райфа) рассмотренный подход к решению многокритериальных задач находит ограниченное применение. И прежде всего это связано с необходимостью длительной и напряженной работы с ЛПР. А как известно, руководители - народ занятой, да и далеко не все из них могут высказывать непротиворечивые суждения. Проблема многократно усложняется в ситуациях группового принятия решений. В то же время следует отметить главное достоинство метода: функция полезности наиболее полно и адекватно отражает систему ценностей ЛПР и позволяет относительно просто находить решение, наиболее предпочтительное (и в этом смысле оптимальное) для ЛПР с помощью одной стандартной задачи оптимизации.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.009 с.) |


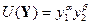 ,
,  >0,
>0,  >0.
>0. ,
,  ) равен
) равен  , если ЛПР согласен уступить
, если ЛПР согласен уступить  единиц критерия y 1 за
единиц критерия y 1 за  единиц критерия у 2, где
единиц критерия у 2, где 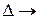 0). В общем случае предельные коэффициенты замещения зависят от значений y 1 и у 2. Возвращаясь к рис.10.4 нетрудно понять, что предельный коэффициент есть тангенс угла наклона касательной к кривой безразличия в точке (
0). В общем случае предельные коэффициенты замещения зависят от значений y 1 и у 2. Возвращаясь к рис.10.4 нетрудно понять, что предельный коэффициент есть тангенс угла наклона касательной к кривой безразличия в точке ( ,
,  ), взятый с обратным знаком. Отсюда ясно, что определение коэффициентов замещения дает представление о карте безразличия, а следовательно, и о виде функции полезности.
), взятый с обратным знаком. Отсюда ясно, что определение коэффициентов замещения дает представление о карте безразличия, а следовательно, и о виде функции полезности. y 2 =Const,
y 2 =Const, Возможный путь получения U 2 (y 2 ) состоит в следующем. Примем произвольно U 2 (
Возможный путь получения U 2 (y 2 ) состоит в следующем. Примем произвольно U 2 (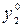 )=0, что дает точку отсчета значений U 2. Тогда U 2 (
)=0, что дает точку отсчета значений U 2. Тогда U 2 ( Из ситуаций, когда коэффициент замещения зависит от значений обоих критериев, рассмотрим самую простую: структура предпочтений ЛПР аддитивна. Обратимся к рис 10.6. Если вместо знака вопроса (?) ЛПР поставит d, т.е. он согласен заплатить d единиц у 1 за увеличение у 2 на с в точке D и это остается в силе при любых значениях а, b, с и d и в любых точках А, В, С и D, образующих прямоугольник, то имеет место условие соответственных замещений.
Из ситуаций, когда коэффициент замещения зависит от значений обоих критериев, рассмотрим самую простую: структура предпочтений ЛПР аддитивна. Обратимся к рис 10.6. Если вместо знака вопроса (?) ЛПР поставит d, т.е. он согласен заплатить d единиц у 1 за увеличение у 2 на с в точке D и это остается в силе при любых значениях а, b, с и d и в любых точках А, В, С и D, образующих прямоугольник, то имеет место условие соответственных замещений. ) эквивалентна по разности полезности
) эквивалентна по разности полезности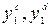 ), где
), где  <
<  и
и 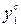 <
<  , если для любого исходного
, если для любого исходного ] значений критерия yi называется точка, которая образует
] значений критерия yi называется точка, которая образует ] и [
] и [ 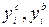 ].
]. . Полагая, что структура предпочтений ЛПР аддитивна (на основе соответствующих предварительных исследований), функцию полезности представим в виде
. Полагая, что структура предпочтений ЛПР аддитивна (на основе соответствующих предварительных исследований), функцию полезности представим в виде )=0, Ui(
)=0, Ui( )= 1, (10.12)
)= 1, (10.12) >0,
>0,  интервала [
интервала [  ] и полагаем U 1 (y
] и полагаем U 1 (y 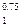 интервала [у
интервала [у  ] и полагаем U 1 (y
] и полагаем U 1 (y  интервала [
интервала [  ] и принимаем U 1 (y
] и принимаем U 1 (y  ) и (
) и ( ). Тогда
). Тогда . (10.14)
. (10.14)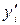 и
и  определяются по построенным графикам. Добавив к (10.14) равенство (10.13), находим значения
определяются по построенным графикам. Добавив к (10.14) равенство (10.13), находим значения  .
.


