
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак оптимальности. Определение начального базисного решения.Содержание книги
Поиск на нашем сайте Имея текущее базисное решение, неоходимо выяснить, является ли оно оптимальным. При положительном ответе процедура поиска оптимума завершается. В противном случае значение критерия может быть улучшено при правильном выборе нового опорного решения (смежной вершины). Признак оптимальности и позволяет установить статус решения и определить последующие действия. Он легко выводится из связи смежных решений. Пусть на k- й итерации получили базисное решение x(k ) с критерием L(k). При смещении из этой вершины на ребро (см. рис.4.6 -а) решение изменяется согласно (4.11): xk+1i=Xki-qair, i=1, 2,…,m. xk+1r=q. Используя приведенные соотношения, определим критерий в новом решении:
или, введя обозначения
получаем
Параметр Δ r называют относительной оценкой переменной. Ее смысл очевиден, если вспомнить, что q - значение новой переменной. Δ r показывает, как изменится значение критерия при введении единицы новой переменной (q= 1 ). Поэтому, если есть отрицательные оценки, текущее решение может быть улучшено при введении в число базисных соответствующей переменной. Если же все оценки будут больше или равны нулю, то тогда ни одна переменная не может улучшить текущее решение, следовательно, условие "Δ j ³0 и является признаком оптимальности. Покажем, что для базисных переменных относительные оценки равны нулю. Так как базисный вектор не выражается через другие, то только один коэффициент arr =1, остальные равны нулю. Из (4.14) следует zr=Cr, а из (4.15) - Δ r= 0. Таким образом, достаточно проверять знаки оценок только небазисных переменных. Полученным формулам можно дать экономическую интерпретацию. Пусть рассматривается задача планирования, в которой Х j – количество продукции j- го вида, Cj – стоимость единицы произведенной продукции. Тогда X (0 ) – план производства, включающий первые m видов продукции.Попытаемся изменить этот план. Включим в него еще один вид продукции r. Так как ресурсы не меняются, это возможно только при одновременном уменьшении продукции, входящей в план X (0). Величина этого изменения определяется коэффициентами air Действительно, как следует из (4.11), air показывает, насколько должно измениться производство продукции i- го вида при введении в план единицы продукции r. В экономической литературе такой показатель называют маргинальной нормой замещения. Значит, объем выпуска каждого вида продукции сокращается на air, а суммарная стоимость на величину Если несколько переменных имеют отрицательные оценки, то возникает необходимость выбора из них самой перспективной. Очевидно, что наибольшее улучшение критерия на очередном шаге даст переменная, для которой произведение q0 Δ j минимально. Однако такой выбор требует большого объема вычислений, так как для каждой переменной с отрицательной оценкой требуется находить q0, а таких переменных в реальной задаче могут быть тысячи. Поэтому обычно выбирают переменную с наименьшей оценкой. Таким образом, укрупненно можно выделить следующие этапы симплекс-метода: 1. Построение начального неотрицательного базисного решения. 2. Анализ оценок. При этом возможны три ситуации: а) все оценки неотрицательны, следовательно, вычисления прекращаются, так как выполнился признак оптимальности. б) имеются отрицательные оценки, но, по крайней мере, одной их них (например, Δ j) соответствует вектор, для которого все коэффициенты разложения неположительны (" aij £0). В этом случае q не ограничено сверху и,как следует из (4.16), критерий неограниченно возрастает. Решение прекращается. в) для каждой отрицательной оценки есть aij >0. Решение может быть улучшено выполнением 3 этапа. 3. Переход к новому базисному решению путем введения переменной с минимальной оценкой и выводом переменной, на которой достигается минимум в (4.12). Этапы 2 и 3 повторяются до выполнения одного из условий останова. Из перечисленных этапов не раскрытым остался первый этап, рассматриваемый ниже.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |


 (4.14)
(4.14) (4.15)
(4.15)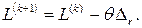 (4.16)
(4.16) Поэтому Zr трактуют как маргинальную цену (снижение стоимости произведенной продукции на каждую единицу продукции r). В то же время, единица продукции r дает прирост стоимости Сr, называемый маргинальным доходом. Очевидно, что если Cr > Zr, то есть Δ r< 0, то такая корректировка плана выгодна.
Поэтому Zr трактуют как маргинальную цену (снижение стоимости произведенной продукции на каждую единицу продукции r). В то же время, единица продукции r дает прирост стоимости Сr, называемый маргинальным доходом. Очевидно, что если Cr > Zr, то есть Δ r< 0, то такая корректировка плана выгодна.


