
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диалоговые методы решения задач по многим критериямСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Главный недостаток рассмотренных выше методов состоит в том, что в большинстве реальных ситуаций ЛПР не располагает до решения задачи информацией о ее свойствах, достаточной для надежного назначения требуемых от него величин. Поэтому, как правило, этими методами не удается за один раз получить приемлемое решение. А многократное применение с корректировкой назначаемых величин фактически переводит их в разряд интерактивных, но не приспособленных для дружественного общения с ЛПР, методов. Интерактивный процесс решения многокритериальной задачи реализуется путем диалога ЛПР с компьютером. При этом происходит чередование этапов вычислений, выполняемых компьютером, и корректировки и принятия решений ЛПР. Такая процедура позволяет ЛПР более полно и глубоко оценить взаимосвязи критериев и возможности оптимизируемой системы. Более того, в интерактивном процессе может развиваться формирование предпочтений, компромиссов и даже системы ценностей. Все это облегчает ЛПР нахождение решения, наилучшего с его точки зрения, и повышает уверенность в правильности выбора. Поэтому такая технология оказывается более реалистичной, более гибкой и более приемлемой для руководителей. Многочисленные интерактивные процедуры предлагают разные схемы решения многокритериальной задачи и предъявляют неодинаковые требования к ЛПР. При прочих равных условиях (сходимость, затраты ресурсов и др.) предпочтительнее те процедуры, которые генерируют только эффективные решения и вызывают у ЛПР меньше затруднений в выражении своих предпочтений. Метод уступок Предварительно ЛПР ранжирует критерии по важности. В результате критериям присваиваются номера в порядке убывания важности. После этого начинается основная часть диалога. Решается задача максимизации первого критерия при Х f 2 ( X ) f 1 ( X ) X
ЛПР оценивает предъявленное ему новое решение X2 и прежде всего улучшение второго критерия, которое определяется как разность в двух решениях: f 2(Х2 )-f 2(X1). За такое увеличение f 2 он платит цену, равную f 3(Х)=> max, f 1(X) f 2(X) X Аналогично формируются задачи по остальным критериям, если их значения не устраивают ЛПР. Очевидно, что в процессе поиска наилучшего решения ЛПР может возвращаться на любое число шагов назад, изменять свои уступки и получать новые решения. Тем самым он выявляет количественные взаимосвязи (замещения) критериев, что облегчает выбор окончательного решения. Пример 10.6. Решим задачу из примера 10.1. Пусть ЛПР представил ранжирование критериев в виде: f 1, f 3, f 2. Максимум f 1 достигается в точке А (рис.10.9), где f 1 ( X ) или в явном виде
В результате допустимое множество сузится до треугольника AMN (рис.10.15). Найдем решение, максимизирующее f 3 на этоммножестве. Оно лежит в вершине N, где f 1=5, f 3=-12,5 и f 2=7,5.Таким образом, за счет снижения первого критерия на 7 единиц увеличилось значение третьего критерия (второго по важности) на 17,5. Однако ЛПР не устраивает значение критерия f 2. Чтобы повысить его, ЛПР согласен уменьшить f 3 до -18, то есть уступает f 3 ( X ) и допустимое множество уменьшается до треугольника NPQ (рис.10.16). Максимизируя f 2, получим решение в точке Q со значениями критериев: f 1=5, f 3=-18, f 2=16. Как видно, второй критерий увеличился на 8,5 за счет снижения третьего на 5,5. Анализируя полученное решение, ЛПР либо принимает его за окончательное, либо, изменив уступки, продолжает поиск. Нетрудно убедиться в том, что решения формируемых задач, если они единственны, принадлежат паретовскому множеству исходной многокритериальной задачи.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 D. Если задача имеет множество оптимальных решений, то на нем ищется решение, наилучшее по второму критерию. Если и оно не единственно, то включается третий критерий, и так до достижения единственного решения. Иначе говоря, ищется лексикографически-оптимальное решение. ЛПР предъявляется полученное решение X1 со значениями всех критериев. ЛПР анализирует это решение и если оно его не устраивает, диалог продолжается. ЛПР просят указать, на какую величину он согласен снизить значение первого критерия с тем, чтобы улучшить значение второго. В результате формируется новая задача:
D. Если задача имеет множество оптимальных решений, то на нем ищется решение, наилучшее по второму критерию. Если и оно не единственно, то включается третий критерий, и так до достижения единственного решения. Иначе говоря, ищется лексикографически-оптимальное решение. ЛПР предъявляется полученное решение X1 со значениями всех критериев. ЛПР анализирует это решение и если оно его не устраивает, диалог продолжается. ЛПР просят указать, на какую величину он согласен снизить значение первого критерия с тем, чтобы улучшить значение второго. В результате формируется новая задача: max,
max, , (10.22)
, (10.22) где
где 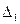 - уступка по первому критерию. Снова ищется лексикографическое решение, начиная с задачи (10.22.).
- уступка по первому критерию. Снова ищется лексикографическое решение, начиная с задачи (10.22.). . Тогда решается задача
. Тогда решается задача , (10.23)
, (10.23) =12, f 3=-30, f 2=18. ЛПР не удовлетворен значением критерия f 3 и готов пойти на снижение критерия f 1 на величину
=12, f 3=-30, f 2=18. ЛПР не удовлетворен значением критерия f 3 и готов пойти на снижение критерия f 1 на величину  - 3 x 1 + 2 x 2
- 3 x 1 + 2 x 2 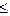 5.
5. =5,5. Тогда условия задачи дополняются еще одним ограничением
=5,5. Тогда условия задачи дополняются еще одним ограничением -18 или - 2 x 1 + 5 х 2
-18 или - 2 x 1 + 5 х 2  18,
18, 



