
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игра двух лиц с нулевой суммой как задача линейного программированияСодержание книги
Поиск на нашем сайте
Рассмотрим платежную матрицу игры двух лиц, не имеющую седловых точек,
где платежи Uij имеют смысл выигрышей игрока A. Как известно, такая игра имеет решение в области смешанных стратегий. Пусть X=(x 1 ,x 2 ,…,xm) – распределение вероятностей на стратегиях игрока A. Тогда согласно принципу гарантированного результата этот игрок будет выбирать такое поведение (распределение X *), которое максимизирует наименьший ожидаемый выигрыш
Обозначим через n минимальный ожидаемый выигрыш
Отсюда очевидно, что n не больше каждого ожидаемого выигрыша, и так как цель – максимальный выигрыш, то приходим к следующей эквивалентной задаче L=n→ max при ограничениях
"хi³0. Это обычная линейная задача, оптимальное значение критерия которой L*=n* есть цена игры. Ее решение определяет оптимальное поведение игрока А. Для игрока B линейная модель строится аналогично, но тот же критерий минимизируется, так как n уже имеет смысл максимального проигрыша, а ограничения на вероятности yj соответствуют строкам платежной матрицы и записываются как неравенства “меньше или равно”. Формы представления задач ЛП и способы приведения к ним Каноническая форма задач ЛП Задача ЛП представлена в канонической форме, если в ее модели все функциональные условия имеют вид равенств и все переменные ограничены по знаку. Направление цели не имеет существенного значения, но для однозначности канонического представления будем иметь в виду максимизацию критерия. Тогда модель задачи ЛП в канонической форме записывается следующим образом
Если использовать векторно-матричные представления, то получим L =
где верхний индекс T означает транспонирование;
Любую задачу ЛП можно привести к каноническому виду. Возможны 3 случая несоответствия исходной модели каноническому представлению. В каждом из них простое преобразование позволяет получить требуемый вид. 1.Если в исходной постановке критерий минимизируется, то изменив знак критерия на обратный, приходим к задаче максимизации, т.е. если 2.В исходной модели есть неравенства. При этом способ преобразования зависит от знака неравенства. В случае неравенства
Отсюда получаем следующее равенство:
Таким образом, чтобы привести рассмотренное неравенство к равенству, нужно к левой части неравенства прибавить новую переменную. Аналогично поступаем с неравенством
и равенство записывается в виде
то есть чтобы неравенство типа “больше или равно” привести к равенству, следует из левой части вычесть новую переменную. В отличие от исходных переменных такие вновь вводимые переменные будем называть дополнительными. Нетрудно видеть, что они по определению являются неотрицательными, что соответствует каноническому представлению модели. 3.Некоторые переменные исходной модели не имеют ограничения на знак. Исключение таких переменных производится следующим способом. Пусть
Таким образом, последние два случая преобразования к каноническому виду приводят к увеличению числа переменных, и поэтому всегда Пример 4.1. Исходная модель:
Каноническая модель:
Стандартная форма задачи ЛП Точные методы решения задач ЛП ориентированы на каноническую форму записи модели. Однако в геометрических представлениях удобнее стандартная форма. Мы будем понимать под стандартной модель, в которой все функциональные ограничения имеют вид неравенств и все переменные неотрицательные. Как и выше, тип экстремума не имеет существенного значения. Таким образом, стандатрная форма модели имеет вид
Та же модель в векторно-матричных обозначениях: L =
Здесь символ / означает “или”. Число переменных Поясним преобразование равенств в неравенства. Пусть в исходной модели имеется q равенств. Решив эту систему уравнений относительно первых q переменных, получим
Используя эти равенства, исключаем
Таким образом, все ограничения задачи будут записаны в виде неравенств.
Основные понятия ЛП. Свойства задач ЛП Множество D={xÎRn| AX£B, X³0} называется допустимым множеством задач ЛП. Иначе говоря, это множество всех решений, удовлетворяющих всем ограничениям задачи. Поэтому форма записи модели не влияет на D. Любое решение Х Î D называют допустимым решением задачи ЛП. Допустимое решение Х* является оптимальным для задачи максимизации, если выполняется неравенство L (X *) ³ L (X), " X Î D. Чтобы определить свойства допустимого множества задачи ЛП, обратимся к терминам теории множеств. Множество называется замкнутым, если оно содержит и свою границу, в противном случае оно открытое. Множество может быть ограниченным, если на нем все переменные ограничены снизу и сверху, и неограниченным, если хотя бы одна переменная на нем не ограничена. Непрерывное множество выпукло, если вместе с любыми двумя точками оно содержит и весь соединяющий их отрезок, иначе множество будет невыпуклым. Пусть условия задачи записаны в стандартной форме å aijxj£ bi, Так как в условия входят только непрерывные переменные, а отношения являются нестрогими, то порождаемое ими множество непрерывно и замкнуто. Возьмем одно неравенство. При двух переменных граница области, где выполняется это неравенство, представляет собой прямую, а множество значений переменных, удовлетворяющих строгому неравенству, расположено с одной стороны границы. Таким образом, неравенству соответствует полуплоскость, которая является выпуклым множесмом. При трех переменных границей будет плоскость, а соответствующее множество – выпуклым полупространством. При большем числе переменных неравенство порождает многомерное выпуклое полупространство с границей – гиперплоскостью. Из теории множеств известно, что пересечение выпуклых множеств выпукло (если оно не пустое). В задаче ЛП число неравенств, а, значит, число полупространств, конечно. Их пересечение и дает допустимое множество D. В связи с этим дадим 2 определения. Пересечение конечного числа выпуклых полупространств, если оно не пустое, называется выпуклым многогранным множеством. Ограниченное выпуклое многогранное множество называется выпуклым многогранником. Характерными примерами выпуклых многогранников являются различные пирамиды и призмы. Таким образом, допустимое множество задачи ЛП может быть или выпуклым многогранным множеством, или выпуклым многогранником, или пустым. Других вариантов быть не может. Критерий L =å CjXj – линейная функция и поэтому удовлетворяет условиям как выпуклости, так и и вогнутости одновременно. Из теории экстремумов известно, что максимум вогнутой функции или минимум выпуклой функции на выпуклом множестве может достигаться только на границе. Аналогичный вывод следует из рассмотрения критических точек целевой функции. Так как производная
то точек, в которых она равна нулю или терпит разрыв, нет. Поэтому, если оптимум существует, то он может быть только на границе. Это важнейшее свойство задач ЛП. Теперь введем понятие разрешимой задачи. Задача ЛП называется разрешимой, если она имеет хотя бы одно оптимальное решение, и неразрешимой в противном случае. Следует обратить внимание на то, что в этом определении не фигурируют допустимые решения, так как их наличие недостаточно для разрешимости задачи, что видно из нижеприводимых утверждений. При решении задач ЛП возможны только три случая: 1) Условия задачи противоречивы (несовместны), допустимое множество пустое и, следовательно, задача неразрешима. 2) Условия задачи совместны, но допустимое множество неограниченно. Тогда возможны два исхода: а) если критерий неограничен на этом множестве, то задача неразрешима; б) если критерий ограничен, то задача разрешима. 3) Условия непротиворечивы и множество является выпуклым многогранником. В этом случае задача всегда разрешима. Из приведенных утверждений, справедливость которых будет показана в следующем разделе, заключаем, что причиной неразрешимости задачи ЛП может быть либо неограниченность критерия, либо противоречивость ограничений. Если модель задачи представлена в каноническом виде, то можно воспользоваться теоремой Кронекера-Капелли для системы линейных уравнений. Согласно теореме система совместна, если ранги основной и расширенной матриц равны, и несовместна в противном случае. Однако из-за трудоемкости вычисления ранга этот способ не используется, а неразрешимость задачи, если она имеет место, обнаруживается в процессе движения к оптимуму или при анализе результатов.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

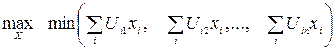 .
.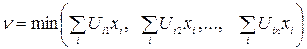 .
.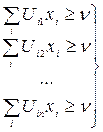
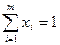 ,
,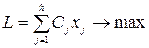
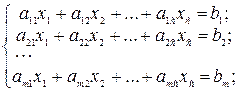

 max
max или
или 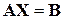
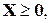
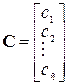 – вектор коэффициентов целевой функции;
– вектор коэффициентов целевой функции; 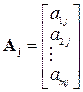 – векторы условий, j =
– векторы условий, j = 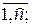
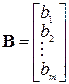 – вектор ограничений или вектор свободных членов, иногда используют сокращение ССЧ (столбец свободных членов);
– вектор ограничений или вектор свободных членов, иногда используют сокращение ССЧ (столбец свободных членов);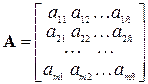 – матрица условий;
– матрица условий;  – вектор переменных;
– вектор переменных; 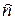 – число переменных в канонической форме, оно не меньше числа переменных в исходной модели
– число переменных в канонической форме, оно не меньше числа переменных в исходной модели 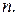
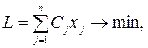 то
то 
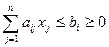 очевидно, что разность правой и левой части будет неотрицательной и неизвестной величиной, которую можно принять за новую переменную:
очевидно, что разность правой и левой части будет неотрицательной и неизвестной величиной, которую можно принять за новую переменную: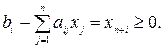
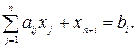
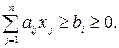 Но теперь новая переменная обозначает разность левой и правой части
Но теперь новая переменная обозначает разность левой и правой части

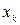 – переменная, которая может иметь любой знак. Введем две неотрицательные переменные
– переменная, которая может иметь любой знак. Введем две неотрицательные переменные 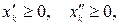 и во всей модели заменяем
и во всей модели заменяем 

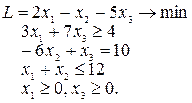
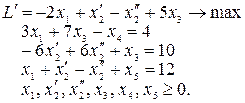

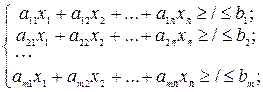
 или
или 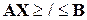
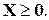
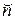 при отсутствии неограниченных по знаку переменных не больше
при отсутствии неограниченных по знаку переменных не больше 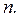 Соответственно матрица
Соответственно матрица 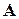 и вектор
и вектор 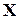 имеют меньшие размеры, чем в канонической модели.
имеют меньшие размеры, чем в канонической модели.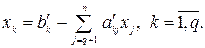
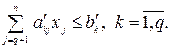
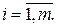
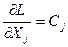 = Const,
= Const,


