
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрирование коэффициентов линейной формыСодержание книги
Поиск на нашем сайте
Здесь рассмотрим три варианта параметрирования, отличающихся своими возможностями. 1. Коэффициенты критерия изменяются линейно от параметра: C (l)= C + l V, а вектор V задается аналогично случаю изменения ресурсов. Тогда задача параметрирования имеет вид: (С +l V)T X ®max AX £ B X ³ 0. Запишем соответствующую двойственную задачу: B T U ®min A T U ³ C +l V U ³ 0 Очевидно, что она представляет собой задачу параметрирования вектора ограничений, решение которой может быть получено вышеописанным методом. В результате найдем диапазон изменения параметра l (0 £ l <
2. Для небазисных переменных весьма просто можно определить диапазон изменения Cj, в котором оптимальное решение остается неизменным. Действительно, пока при изменения Cj все Δj ³0 оптимальное решение исходной задачи сохраняет свой статус. Так как Δ j = Zj-Cj, то уменьшение Cj не может изменить знак оценки. Поэтому интерес представляет увеличение Cj. Пусть Δ ’j = Zj – Cj - ej = Δ j - ej ³ 0. Отсюда следует, что при ej £ Δj исходное решение остается оптимальным. 3. Этот вариант основан на формуле вычисления относительных оценок в модифицированном симплекс-методе:
Она позволяет исследовать влияние изменения любых коэффициентов Сj. В общем случае эти коэффициенты являются некоторыми функциями параметра l: Cj (l). Тогда условия оптимальности запишутся в виде
Здесь обратная матрица соответствует оптимальному базису. Пока при изменении коэффициентов (т.е. l) эти неравенства выполняются, оптимальное решение не изменяется. Значение l, при котором хотя бы одно из условий становится равенством, и будет критическим. Практически оно находится так: каждое условие записывается как равенство и определяются его корни; из всех корней выбирается наименьшее положительное. Это и будет Очевидно, что данный вариант параметрирования пригоден как для линейных, так и нелинейных зависимостей от параметра. Однако в последнем случае его применение ограничено возможностью нахождения корней нелинейного уравнения. Пример 4.8. Пусть ожидается изменение коэффициентов критерия в примере 4.2 (разд. 4.9.7) по закону: C 1(l)=7 - 2 l, C 2(l)=5 + l. Необходимо определить критическое значение l, если таковое имеется. В оптимальной симплекс-таблице базисные индесы расположены в следующем порядке: 6, 2, 5, 1. Значит,
Из условий оптимальности Δ3³0, Δ4 ³0 записываем уравнения
Первое уравнение имеет отрицательный корень, корень второго равен 11/8. Таким образом, Как отмечалось выше, параметрические решения могут быть получены также при одновременном изменении правых частей и коэффициентов критерия по линейной зависимости от одного параметра
при линейном изменении столбца условий Aj + l Vj или строки a i+ l V i. В других случаях изменения модели поведение оптимального решения определяется решениями задачи одним из методов ЛП при разных значениях изменяемых параметров модели.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 ), в котором базис двойственной задачи остается неизменным. В строке Z оптимальной таблицы двойственной задачи находятся переменные прямой задачи (двойственные к двойственной). Но значения zj зависят только от базиса, поэтому в найденном диапазоне l оптимальное решение также не меняется. Изменяться будет только критерий. При достижении критического значения l произойдет смена базиса (оптимальной вершины), а значит, и оптимального решения прямой задачи. Проследить дальнейшее изменение решения можно после повторного решения двойственной задачи с векторм
), в котором базис двойственной задачи остается неизменным. В строке Z оптимальной таблицы двойственной задачи находятся переменные прямой задачи (двойственные к двойственной). Но значения zj зависят только от базиса, поэтому в найденном диапазоне l оптимальное решение также не меняется. Изменяться будет только критерий. При достижении критического значения l произойдет смена базиса (оптимальной вершины), а значит, и оптимального решения прямой задачи. Проследить дальнейшее изменение решения можно после повторного решения двойственной задачи с векторм 
 Такое поведение следует и из геометрических представлений (рис. 4.14). Изменение коэффициентов линейной формы изменяет наклон линии уровня критерия, но не влияет на допустимое множество. При наличии критических значений l изменение коэффициентов приводит к скачкообразному изменению оптимального решения – переходу из вершины в вершину (смежную).
Такое поведение следует и из геометрических представлений (рис. 4.14). Изменение коэффициентов линейной формы изменяет наклон линии уровня критерия, но не влияет на допустимое множество. При наличии критических значений l изменение коэффициентов приводит к скачкообразному изменению оптимального решения – переходу из вершины в вершину (смежную). + ej, ej ³.0. Тогда
+ ej, ej ³.0. Тогда .
.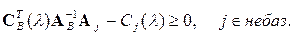

 Вычисляем:
Вычисляем: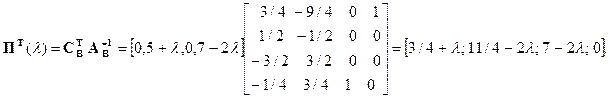

 До этого значения l оптимальное решение не изменяется, при l =11/8 имеем альтернативные оптимальные решения (линии уровня L(
До этого значения l оптимальное решение не изменяется, при l =11/8 имеем альтернативные оптимальные решения (линии уровня L(



