
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрия задач ЛП, базисные решения, вырожденность.Содержание книги
Поиск на нашем сайте Геометрические представления позволяют лучше уяснить рассмотренные свойства задач ЛП. Размерность пространства задачи k равна разности числа переменных и числа ограничений-равенств. Поэтому для модели в стандартной форме k= Очевидно, что геометрические построения возможны для k £ 3. Сначала мы рассмотрим задачи на плоскости (k= 2), а затем сделаем обобщение на многомерное пространство. В качестве первого примера решим графически задачу оптимального планирования из разд. 4.2.2:
Чтобы решить задачу, надо сначала построить допустимое множество, а затем по целевой функции найти на нем точку или множество с максимальным значением критерия. Допустимое множество задачи находится как пересечение допустимых множеств, построенных по отдельным условиям задачи. В нашем примере таких множеств 6. Построение множества начинается с определения его границы. Возьмем условия неотрицательности переменных: x 1³0, следовательно, уравнение границы x 1 =0 (ось х 2) и допустимое множество – правая полуплскость (включая границу); х 2³0, уравнение границы х 2=0 (ось x 1), допустимое множество – верхняя полуплоскость. Таким образом, при неотрицательности всех переменых допустимое множество задачи ЛП всегда лежит в первом квадранте. Теперь перейдем к построению допустимых множеств по функциональным условиям. Граница по 1-му условию 2 х 1+3 х 2=19 (из канонической модели имеем альтернативное уравнение x 3=0) представляет собой прямую, для построения которой достаточно нанести любые 2 точки. Например, положив х 1=0, из уравнения получим х 2=19/3 (точка на оси х 2); вторую точку возьмем на оси х 1: х 2=0 и тогда х 1=19/2. Чтобы определить, с какой стороны прямой выполняется условие, достаточно проверить одну точку вне границы. В качестве такой точки проще всего брать начало коодинат, в котором левая часть условия всегда равна нулю.. Наше условие 1) выполняется в этой точке, следовательно, допустимое множество – юго-западная полуплоскость. В противном случае получили бы северо-восточную полуплоскость. Аналогично записываем уравнения границ и проводим соответствующие прямые по условию 2): из исходной модели 2 х 1+ х 2=13 и канонческой модели х4 =0; по условию 3): 3 х 2=12 и х5 =0; по условию 4): 3 х 1=17 и х6 =0. Нетрудно убедиться, что каждое из этих условий выполняется с той стороны своей границы, с которой находится начало коодинат.
Из бесконечного множества допустимых решений, принадлежащих этому многоугольнику, необходимо найти то, которое дает максимум критерия. Для этого нам нужно знать “поведение“ критерия на допустимом множестве. С этой целью построим линии уровня критерия L=Const.. Так как критерий линейный, то линии уровня – это множество параллельных прямых с постоянным градиентом (направлением возрастания значений критерия). Поэтому для определения этого направления достаточно иметь 2 линии уровня. Конкретные значения L можно брать любые, но так, чтобы соответствующие прямые оказались в области уже выполненных построений.
2 x* 1+3 x* 2=19, 2 x* 1+ x* 2=13. Отсюда имеем: х* 1=5, х* 2=3. Значения остальных переменных вычисляются однозначно из канонической модели после подстановки в ее уравнения х* 1и х* 2. В результате получаем оптимальное решение задачи: х* 1=5, х* 2=3, х* 3= х*4 =0, х*5 =3, х*6 =2 и, следовательно, L*= 50. Таким образом, чтобы добиться максимальной прибыли в 50 единиц, необходимо производить 5 изделий первого типа и 3 изделия второго типа. При этом будут полностью использованы ресусы 1-го и 2 -го вида (х* 3= х*4 =0), а по ресурсам 3-го и 4-го вида образуются остатки в количестве 3 и 2 соответственно (х*5 =3, х*6 =2). Задача имеет единственное оптимальное решение, так как линия уровня L= 50 соприкасается с допустимым множеством только в одной точке.▲
Очевидно, что при данном допустимом множестве задача всегда будет иметь решение независимо от коэффициентов целевой функции, потому что в любом случае будет существовать предельное положение линии уровня критерия. Однако оптимальное решение может быть и не единственным. Пусть в нашем примере при тех же ограничениях изменились коэффициенты критерия: L 1=4 x 1+6 x 2→ max.
Теперь выясним, что будет, если допустимое множество неограниченно. Не конкретезируя модель, рассмотрим поведение двух целевых функций на одном неограниченном множестве (рис. 4.4). Направление улучшения критериев показано стрелками. Здесь мы видим разное поведение критериев, приводящее к различным результатам. а) Значение критерия L 1 улучшается в направлении неограничености множества и, следовательно, критерий неограничен на допустимом множестве, то есть он может улучшаться до бесконечности – допустимые решения есть, а оптимального нет. б) Улучшение критерия L 2 ограничено на допустмом множестве, следовательно, решение существует (в этом примере оно единственное, но, очевидно, возможны и множественные решения на неограниченном множестве).
Результаты геометрического анализа задачи ЛП в двумерном простанстве легко обобщаются на многомерное пространство. Вместо прямых границами множеств будут гиперплоскости, а непустым допустимым множством задачи – выпуклый многогранник или выпуклое многогранное множество. Для нахождения решения мысленно перемещаем гиперплоскость уровня критерия в направлении его улучшения пока имеютя общие точки с допустимым множеством. Если достигается предельное положение, то задача разрешима. При этом гиперплоскость может касаться только одной вершины множества – задача имеет единственное решение,ребра или грани допустимого множества – существует множество решений соответственно на ребре или грани, которые полностью определяются своими крайними точками (вершинами). При отсутствии предельного положения критерий неограниченно улучшается и задача неразрешима. Таким образом, если задача ЛП разрешима, то оптимальное решение обязательно достигается в вершине допустимого множества. Поэтому оптимальное решение следует искать не на всей границе, а только в вершинах допустимого множества.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.006 с.) |

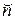 , а для канонической модели k=
, а для канонической модели k= 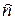 - m. Как отмечалось раньше, значение k не зависит от формы записи модели и является фиксированным для конкретной задачи.
- m. Как отмечалось раньше, значение k не зависит от формы записи модели и является фиксированным для конкретной задачи.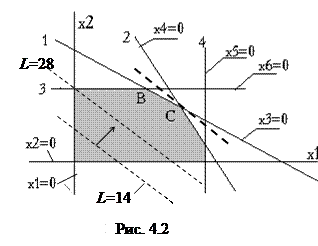 Находя пересечение шести построенных допустимых множеств, получаем выпуклый шестиугольник (рис. 4.2) – частный случай выпуклого многогранника.
Находя пересечение шести построенных допустимых множеств, получаем выпуклый шестиугольник (рис. 4.2) – частный случай выпуклого многогранника. Так как условия не изменились, то допустимое множество остается прежним. Если повторить построение линий уровня, то они будут параллельны стороне BC (коэффициеты при перемен-ных в критерии и 1-м ограничении пропорциональ-ны). Поэтому в предельном положении линия уровня критерия совпадает с границей по 1-му ограничению (рис. 4.3). В таком случае получим множество (бесконечное) оптимальных решений, лежащее на стороне BC, каждому из которых соответствует одно и то же максимальное значение критерия L 1.
Так как условия не изменились, то допустимое множество остается прежним. Если повторить построение линий уровня, то они будут параллельны стороне BC (коэффициеты при перемен-ных в критерии и 1-м ограничении пропорциональ-ны). Поэтому в предельном положении линия уровня критерия совпадает с границей по 1-му ограничению (рис. 4.3). В таком случае получим множество (бесконечное) оптимальных решений, лежащее на стороне BC, каждому из которых соответствует одно и то же максимальное значение критерия L 1. Приведенные построения подтверждают высказанное ранее утверждение о том, что на ограниченном допустимом множестве (выпуклом многограннике) задача всегда разрешима.
Приведенные построения подтверждают высказанное ранее утверждение о том, что на ограниченном допустимом множестве (выпуклом многограннике) задача всегда разрешима. Рассмотрим другой случай (рис. 4.5). Пересечение допустимых множеств, порождаемых тремя функциональными ограничениями задачи и условиями неотрица-тельности переменных, оказывается пустым. Следовательно, допустимых решений нет и задача неразрешима.
Рассмотрим другой случай (рис. 4.5). Пересечение допустимых множеств, порождаемых тремя функциональными ограничениями задачи и условиями неотрица-тельности переменных, оказывается пустым. Следовательно, допустимых решений нет и задача неразрешима.


