Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод декомпозиции Данцига - ВулфаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При решении задач большой размерности значительная часть времени тратится на обращения к внешней памяти и это является главным препятствием на пути увеличения размерности задач. Уменьшить число обращений к внешней памяти можно, если удается большую задачу заменить рядом задач существенно меньшей размерности. Приемы и методы, позволяющие выполнять такие преобразования, составляют предмет блочного программирования. Одним из эффективных методов блочного программирования применительно к линейным задачам является метод декомпозиции Данцига – Вулфа. По данным авторов метод позволяет решать задачи с размерностью n~ 106, m~ 105.
Сначала рассмотрим математические преобразования, приводящие к разбиению исходной задачи, а затем покажем, в каких случаях это дает эффект по сравнению с непосредственным решением большой задачи. Пусть имеется следующая модель задачи: L= C T X àmax; (6.1) AX = B; (6.2) X ³0, (6.3) где вектор X имеет размерность n, а вектор B – m. Условия (6.2), (6.3) определяют допустимое множество задачи D. Представим матрицу А и вектор В в виде двух подматриц:
Тогда условия задачи (6.2)-(6.3) записываются следующим образом: А (0) Х = В (0); (6.4) А (1) Х = В (1); (6.5) Х ³0 (6.6) Условия (6.4), включающие m0 равенств, порождают допустимое множество D0, а система (6.5) содержит m1 равенств и вместе с (6.6) задает множество D1. Очевидно, что m=m0+m1, D = D0 Ç D1. При этом выделение подматриц выполняется так, что m1 >> m0. Далее будем полагать, что множество D1 ограниченное и, значит, является выпуклым многогранником. В противном случае его легко сделать ограниченным добавлением ограничений сверху на переменные так, что они не повлияют на исходное множество D. Предположим, что нам известны вершины множества D1. Обозначим их координаты через Х 1, Х 2,…, Х N, где N – число вершин. Поскольку D1 – выпуклый многогранник, то любую его точку можно представить в виде линейной комбинации вершин: Х = S z n=1; (6.8) z n³0, " v. (6.9) Так как все решения Х, определяемые по (6.7)-(6.9), принадлежат D1, то описание (6.7)-(6.9) эквивалентно (6.5), (6.6). Подставим Х в виде (6.7) в (6.1) и (6.4): L = S A (0) X n z n= B (0). Считая X n известными, введем обозначения: С Т Х n= sn; (6.10) А (0) Х n= Р n. (6.11) Тогда преобразованная модель задачи запишется в виде L =
" z n³0. В этой модели неизвестными являются z n, число которых равно числу вершин многогранника D1. Последнее равенство модели можно объединить со всеми остальными, используя обозначения расширенных векторов
Тогда окончательно получим: L =
" z n³0. (6.15) Задача в виде (6.13) – (6.15) называется координирующей или основной задачей. Главное отличие этой задачи от исходной в несравнимо меньшем числе условий (m0 +1<< m). Если мы сможем ее решить, то есть найти Z *, то получим решение и исходной задачи, воспользовавшись (6.7): Х *= Для решения основной задачи применим модифицированный симплекс-метод. Начальное решение можно построить, не зная ни одной вершины, с помощью искусственных переменных zN+i. Согласно модифицированному методу после получения очередного базисного решения вычисляются относительные оценки. В разд. 4.10 получены формулы:
Перепишем их в обозначениях координирующей задачи:
или окончательно
Мы не можем вычислить все оценки, так как нам не известно даже их число. Но этого и не требуется, достаточно только определить: есть или нет среди них отрицательные. Для ответа на этот вопрос будем искать наименьшую оценку. Если она отрицательная, текущее решение координирующей задачи может быть улучшено введением переменной с этой оценкой. В противном случае констатируется выполнение признака оптимальности. Итак, задача состоит в следующем: Dnàmin. Отбросив в (6.18) константу, запишем ее в виде (pTA(0)-CT)Xn® Решение задачи (6.19) проблематично, так как минимум ищется на дискретном множестве вершин многогранника D1. Учитывая, что минимизируемая функция линейная, будем искать решение не на вершинах, а на всем многограннике. Известно, что если решение существует, то оно будет достигаться в вершине. Поэтому решение на всем (непрерывном) множестве D1 совпадет с решением задачи (6.19). Таким образом, задачу (6.19) заменяем эквивалентной: Lвсп =(pTA(0)-CT)X® A(1)X = B(1); (6.21) X ³ 0. (6.22) Эта задача называется вспомогательной. Если она неразрешима, то и исходная задача не имеет решения. Пусть оптимальное решение вспомогательной задачи (6.20)-(6.22) достигается в вершине r. Это означает, что нам становятся известны координаты вершины Xr и оптимальное значение критерия
Очевидно, что если D r ³0, то и все оценки неотрицательны, и решение координирующей задачи завершено. При отрицательной D r решение продолжается. В базис основной задачи вводится вектор
Направляющий столбец находится разложением этого вектора по текущему базису:
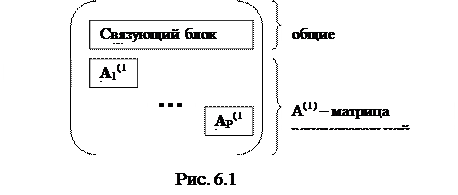
После определения направляющего элемента и симплекс-преобразования получаем новое решение основной задачи. Коэффициент критерия (6.13) при переменной, введенной в базисное решение, вычисляется согласно (6.10): sr = C T X r. (6.32) Теперь по формуле (6.17) находим новый вектор Таким образом, решение исходной задачи заменяется многократным решением основной и вспомогательной задач. При этом порядок размерности вспомогательной задачи такой же, как у исходной. Поэтому естественнен вопрос: в каких случаях такой метод эффективен? Ответ очевиден: в тех случаях, когда сложность решения вспомогательной задачи намного ниже, чем исходной. Такие случаи имеют место, когда матрица условий задачи (после упорядочения строк и столбцов) оказывается почти-блочно-диагональной, как показано на рис. 6.1. Примером может служить задача планирования производства продукции в крупной фирме или холдинге, когда у каждого предприятия своя номенклатура продукции, а некоторые ресурсы являются общими. Подматрица А (0), входящая в параметры координирующей задачи,соответствует ограничениям по общим ресурсам. Такие условия называют связующими. Их относят к основной задаче.
Остальные условия образуют вспомогательную задачу. При этом подматрица А (1) имеет блочно-диагональную структуру, что позволяет разбить вспомогательную задачу на p независимых задач:
После решения этих задач определяется критерий вспомогательной задачи по очевидной формуле
Таким образом, решение вспомогательной задачи существенно упрощается, если структура матрица условий может быть приведена к блочно-диагональной. В следующем разделе декомпозиция вспомогательной задачи будет показана на примере решения транспортной задачи. Применение рассмотренного метода может быть целесообразно и тогда, когда вспомогательная задача имеет особенности, позволяющие решать ее специальными методами.
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.008 с.) |


 z n X n; (6.7)
z n X n; (6.7) s n z nàmax;
s n z nàmax; P n z n= B (0);
P n z n= B (0); z n=1;
z n=1; . (6.12)
. (6.12) z n =
z n =  ; (6.14)
; (6.14) z n* X n. (6.16)
z n* X n. (6.16)

 (6.17)
(6.17)
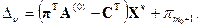 (6.18)
(6.18) (6.19)
(6.19) (6.20)
(6.20) . Тогда согласно формуле (6.18) вычисляем минимальную оценку
. Тогда согласно формуле (6.18) вычисляем минимальную оценку (6.23)
(6.23) , определяемый по формуле
, определяемый по формуле (6.30)
(6.30) . (6.31)
. (6.31) , снова решаем вспомогательную задачу и по полученной минимальной оценке делаем вывод о дальнейших действиях.
, снова решаем вспомогательную задачу и по полученной минимальной оценке делаем вывод о дальнейших действиях.