
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерактивное компромиссное программированиеСодержание книги
Поиск на нашем сайте Так называется метод, использующий для поиска удовлетворящего ЛПР компромиссного решения линейную свертку. При этом от ЛПР не требуется назначать веса, ему лишь нужно на каждой итерации выбрать одно решение из (m +1)-го предлагаемых, после чего веса вычисляются программно. Сравнивать альтернативные решения легче, если критерии измеряются в одной шкале. С этой целью в данном методе критерии заменяются функциями степени близости, которые определяются по формуле
где Теперь паретовские (эффективные) решения можно находить, максимизируя свертку
при условии Х Одним из существенных недостатков ряда интерактивных методов является использование параметров, численные значения которых должен указывать ЛПР. В рассматриваемом методе эта проблема исключается, так как веса в (10.25) определяются не ЛПР, а специальной процедурой, обеспечивающей вычисление на каждой итерации значений весов, оптимальных в максиминном смысле. Процедура основана на игровом подходе, а именно, на формализации и решении игры двух лиц с нулевой суммой. В качестве стратегий первого игрока рассматриваются целевые функции, второго - решения многокритериальной задачи, полученные к данному шагу и не забракованные ЛПР. Платежом на каждой паре стратегий В целом процесс поиска компромиссного решения рассматриваемым методом можно представить следующим образом. Процедура начинается с решения 2 m обычных задач математического программирования для нахождения максимальных и минимальных значений m целевых функций. По ним вычисляют степень близости каждого решения к максимально возможному значению каждой целевой функции. Приняв их за платежи игры 2-х лиц размерности m* m и решив игровую задачу, получают текущие веса целевых функций. Последние используют для нахождения (m +1)-го решения. Для полученного решения также вычисляются степени близости по всем критериям. Теперь вместе с предыдущими m решениями новое решение предъявляют ЛПР. Его спрашивают, предпочитает ли он одно из этих решений всем другим. Если да, то это решение принимается за окончательное и процесс заканчивается. В противном случае ЛПР просят выделить из предъявленных ему решений наименее предпочитаемое. Это решение исключается, а из оставшихся m решений формируется и решается очередная игровая задача. Далее таким же способом, как описано выше, находят новое альтернативное компромиссное решение и предъявляют его вместе с m уже имеющимися. Итеративный процесс продолжается до тех пор, пока ЛПР не выявит предпочитаемое им решение. Рассмотренная процедура реализуется следующим алгоритмом. Шаг 0. Определить а) при условии Х б) при условии X Шаг 1. Взять решения Построить таблицу
где Шаг 2. Решить следующую игровую задачу одним из методов линейного программирования.
при условиях
...
Шаг 3. Образовать новую функции свертки, используя оптимальные веса, найденные на шаге 2, и решить следующую задачу максимизации этой функции для получения нового альтернативного компромиссного решения
при условии X Шаг 4. Вычислить значения степеней близости нового решения к максимально возможным значениям целевых функций, Шаг 5. Представить ЛПР новую таблицу и спросить, предпочитает ли он строго одно решение всем другим m-решениям. Если да, то идти на шаг 6. Иначе просить ЛПР отметить наименее предпочитаемое решение. Заменить его новым решением, найденным на шаге 4, и вернуться на шаг 2. Шаг 6. Останов. Пример 10.7. Применим этот алгоритм к задаче из примера 10.5. Шаг 0. a) при условии X где D определяется системой x 1+ x 2 - x 1+ x 2 0 Решение: f 2(X) = 4 x 1- x 2 при условии X Решение: б) f 1(X ) =-2 x 1+ x 2 при условии X Решение:
при условии X Решение: Шаг 1. Решения
Шаг 2. Решаем задачу линейного программирования:
при условиях
Решение: Шаг 3. Составляем новую функцию свертки
Решаем следующую задачу линейного программирования для нахождения нового компромиссного решения:
при условии X Решение: Х3=(4,4), f 1(Х3)=-4, f 2(X3)=l2. На рис.10.17 это точка С. Шаг 4. Вычисляем степени близости полученного решения
и показываем ЛПР три эффективных решения:
Шаг 5. Предположим, что ЛПР не устраивает ни одно из этих решений, а наименее предпочтительным он считает решение X1. Тогда это решение заменяем решением X3 и возвращаемся на шаг 2. Вторая итерация Шаг 2. Решаем следующую задачу для определения новых весов: d 4(X) => max при условиях 0.571
Оптимальные значения: Шаг 3. Решаем задачу с этими весами: d 4(X) = 0.447 d 1(X) + 0.553 d 2(Х)= = при условии X Решение: Х4=(6.2), f 1(X4)=-10, f 2(X4)=22. На рис.10.17 это вершина E множества достижимости. Шаг 4. Вычисляем степени близости нового решения
и предъявляем его ЛПР вместе с оставшимися:
Шаг 5. Предположим, что ЛПР предпочитает новое решение всем другим. Идем на шаг 6. Шаг 6. Останов. Наилучшее компромиссное решение нашей задачи:
Х =(6.2), f = (-10,22), d = (0.143,0.923). Отметим некоторые особенности рассмотренного метода. При его применении необходимо иметь в виду, что в соответствии с теоремой 5 максимизация линейной свертки (10.25) гарантирует получение эффективного решения только в случае положительности всех Из анализа процедуры поиска компромиссного решения следует, что область принятия решений сужается после каждой итерации алгоритма. При этом можно ожидать хорошей сходимости, так как каждое новое решение, предъявляемое ЛПР, является наиболее вероятным среди уже имеющихся, что обусловлено максиминным выбором весов. Очевидным достоинством метода является использование естественного для ЛПР способа выражения своих предпочтений. Здесь отсутствуют какие-либо эвристические параметры (к ним относят параметры, значения которых должен назначать ЛПР). Если модель исходной многокритериальной задачи линейна, то вся вычислительная часть интерактивного метода может быть реализована с помощью стандартных пакетов линейного программирования, что означает возможность решения задач большой размерности. Подзадача определения оптимальных весов (шаг 2) остается линейной при любом виде исходной модели. Наконец, заметим, что для получения очередного нового решения можно применить вместо линейной максиминную свертку. Такая замена может оказаться существенной для линейных задач, так как линейная свертка позволяет находить решения только в вершинах, в то время как максиминная – и на ребре или грани. И тем самым можно избежать возможных повторений решений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 , (10.24)
, (10.24) - максимальное и минимальное значения
- максимальное и минимальное значения  -го критерия на допустимом множестве D. Как следует из (10.24),
-го критерия на допустимом множестве D. Как следует из (10.24),  может изменяться от 0 до 1. Очевидно, что если
может изменяться от 0 до 1. Очевидно, что если  - линейная функция, то и
- линейная функция, то и  тоже линейная.
тоже линейная. (10.25)
(10.25) D.
D. является степень близости
является степень близости  -м решении к своему максимальному значению
-м решении к своему максимальному значению  . Тогда вероятности применения стратегий первым игроком и будут иметь смысл весов целевых функций, входящих в свертку (10.25).
. Тогда вероятности применения стратегий первым игроком и будут иметь смысл весов целевых функций, входящих в свертку (10.25).
 , для чего решить задачи
, для чего решить задачи
 ) не что иное, как идеальные решения.
) не что иное, как идеальные решения.
 ) называют антиидеальными.
) называют антиидеальными.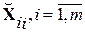 в качестве первоначальных решений
в качестве первоначальных решений  и вычислить степени близости по формуле (10.24).
и вычислить степени близости по формуле (10.24).




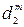



 - степень близости j -ro решения к максимальному значению i -й целевой функции.
- степень близости j -ro решения к максимальному значению i -й целевой функции.




 .
.
 . Добавить колонку с этими значениями к таблице, построенной на шаге 1.
. Добавить колонку с этими значениями к таблице, построенной на шаге 1.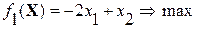
 8,
8, =(0,2),
=(0,2),  =2.
=2.
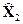 =(6,0),
=(6,0),  =24.
=24.
 =(6,0),
=(6,0),  =-12.
=-12. = 4 x 1- x 2
= 4 x 1- x 2  min
min =(0.2).
=(0.2).  =-2.
=-2.

 ,
, ,
, .
. =0.5,
=0.5,  =0.5.
=0.5.

 ,
,
 + 0.538
+ 0.538  d 4,
d 4, 2
2  d 4,
d 4,
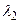 =0.553.
=0.553. ( 2 х 1 + x 2 + 40 )=> max
( 2 х 1 + x 2 + 40 )=> max D.
D. =0.143,
=0.143,  =0.923
=0.923

 . Наличие нулевых значений весов может приводить к слабо эффективным решениям.
. Наличие нулевых значений весов может приводить к слабо эффективным решениям.


