
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Где искать оптимальное решениеСодержание книги
Поиск на нашем сайте Как отмечалось выше, без установления принципа оптимальности, отражающего предпочтения ЛПР, невозможно формально распознать оптимальное решение (как в сказке: "ищи то, не знаю, что"). Однако учитывая стремление ЛПР к увеличению значений всех частных критериев, можно формальными методами исключить из множества G (и D) заведомо не перспективные точки и тем самым облегчить решение задачи.
Это наименование произошло от фамилии итальянского экономиста и социолога В.Парето (1848-1923), который проводил математические исследования процесса рыночного обмена товаров. Рассматривалась модель чистого обмена, в которой каждый участник стремится составить себе набор товаров наибольшей ценности. Эффективным является такое состояние, которое не может быть улучшено путем перераспределения товаров ни для одного из участников без ущемления интересов некоторых других участников. Значит, эффективное состояние соответствует экономическому равновесию, а неэффективное состояние побуждает проводить перераспределение (торговать), которое ведет к установлению равновесия. Теперь очевидно, что оптимальное решение следует искать только среди эффективных точек. При групповом принятии решений множество эффективных точек называют также переговрным, подчеркивая тем самым, что только их и нужно рассматривать в качестве претендентов на компромиссное решение. Если эффективная точка одна (А на рис.10.2), что возможно в тривиальном случае непротиворечивости критериев, то она и является искомым оптимумом. В задачах с конечным числом точек G (дискретные задачи) выделение эффективного множества часто настолько уменьшает число вариантов, что выбор из них наилучшего не вызывает затруднений у ЛПР.
Ввиду особой важности парето-оптимальности для решения многокритериальных задач приведем более строгие определения, связанные с этим понятием. Определения Для описания предпочтений используют бинарные отношения, вводимые на множестве А сравниваемых объектов. В многокритериальной задаче роль таких объектов играют X или Y на множествах D и G соответственно. Если из двух объектов a и b ЛПР выбирает a, то говорят, что a предпочтительнее b. Все пары вида (a,b), где a,bÎА, для которых a предпочтительнее b, образуют множество, называемое отношением строгого предпочтения на А. Такое отношение обозначают символом ý (a ý b или a P b, где Р – первая буква английского слова preferance – предпочтение). Объекты a и b неразличимы для ЛПР, если они одинаковы по предпочтительности. Это значит, что не выполняется ни отношение a ý b, ни b ý a. Множество всех неразличимых пар (a, b) называют отношением неразличимости или безразличия и обозначают символом ~ (a~b или a I b, где I происходит от indifference – безразличие).
При сравнении по предпочтительности векторов Y=f(X ) наиболее просто сопоставлять те вектора, которые отличаются лишь одной компонентой. Однако в общем случае частные критерии yi = fi (X) могут по-разному соотноситься по предпочтительности в зависимости от того, на каких уровнях зафиксированы остальные критерии. Так если вектор ( Задачи, в которых все критерии независимы по предпочтению, а отношением строгого предпочтения R является отношение >= (не меньше) называются многокритериальными задачами максимизации (аналогично при отношении «не больше» – задачами минимизации). Напомним, что R включает (объединяет) P и I. На множестве G (или D) отношение строгого порядка P задают неравенством Y Вектор (решение), оптимальный по отношению ≥ на множестве G (D), называется эффективным или парето-оптимальным. Значит, вектор Y *ÎG является парето-оптимальным (оптимумом Парето), если не существует вектор Y Î G такой, что Y ³ Y*. Множество таких векторов обозначают через Р(Y)и называют множеством Парето (эффективным множеством). Множество эффективных решений обозначают через Р(X). Вектор, оптимальный по отношению >, называют слабо эффективным, слабо оптимальным по Парето (слабым оптимумом Парето). Значит, вектор Y *ÎG слабо парето оптимальный, если не существует Y ÎG такой, что Y>Y*. Множество таких векторов называют слабо эффективным и обозначают через S(Y). Соответствующее множество слабо эффективных решений имеет обозначение S(X ). Если в G не найдётся Y³Y *, то не существует и Y>Y*. Следовательно, всякий эффективный вектор одновременно является и слабо эффективным, т.е. P(Y)ÍS(Y). Аналогично P(X) Í S(X). Различие эффективного и слабо эффективного множеств хорошо видно на рис.10.3. Множество P(Y) состоит из частей границы множества G: кривых bc, de (исключая точки d и e) и gh, аS(Y)– из кривой abcde (включая точку e) и кривой ghk. Точка d не входит в P(Y), т.к. она доминируется точкой c. Точно также точка e менее предпочтительна, чем g. Геометрическое определение множеств P(Y) и S(Y) основано на том, что все точки YÎE m, для которых выполняется неравенство Y³Y0, образуют ортант (для m =2 – прямой угол), стороны которого параллельны координатным осям, а вершиной является точка Y0.
Понятие слабой эффективности оказывается полезным и в случае, когда приходится сокращать первоначальный набор критериев. Нередко на первых этапах исследования трудно определить минимально необходимый набор критериев и поэтому начинают с возможно более полного набора. По мере изучения свойств задачи выявляются несущественные критерии, которые исключаются из дальнейшего рассмотрения. В [30] показано, что множество слабо эффективных решений, выделяемое на полном наборе критериев, содержит все исходные решения, эффективные по сокращенному набору критериев. Условия оптимальности Здесь рассмотрим наиболее важные с точки зрения приложений необходимые и достаточные условия оптимальности. Они позволяют строить методы отыскания эффективных решений и способы проверки эффективности найденных решений. Наиболее общий случай необходимых условий содержит следующая теорема. Теорема 1. Пусть Y *
Условие При оговариваемых свойствах D и f (X) справедливы теоремы 2 и 3. Теорема 2. Пусть D выпукло, а
Теорема 3. Пусть D выпукло, а f вогнуто. Для слабой эффективности точки X *ÎD необходимо и достаточно, чтобы существовали числа
Терема 4. Вектор Y *ÎG эффективен тогда и только тогда, когда для каждого
где
Если Y*Î G эффективна, то она является единственной в G точкой, удовлетворяющей (10.4) при каждом Достаточные условия, приведенные ниже, основаны на свойствах возрастающей функции многих переменных. Поэтому сначала дадим определение такой функции. Числовая функция F (Y), определённая на множестве G, является возрастающей по отношению ³, если из выполнения неравенства Y³Y ¢ для векторов Y,Y¢Î G всегда следует справедливость неравенства F (Y) >F (Y¢). Аналогично, F (Y) – функция, возрастающая по отношению >, если из Y>Y ¢ всегда следует F (Y )>F (Y¢). Теорема 5. Пусть функция F (Y ) определена на множестве G. Для того чтобы точка Y*Î G была эффективной (слабо эффективной), достаточно, чтобы она являлась точкой максимума на множестве G функции F (Y), возрастающей по отношению ³ (по отношению >). Теорема легко доказывается от противного. Пусть Y *ÎG и F (Y*)³ F (Y) для всех Y ÎG. (10.6) Предположим противное, т.е. что существует Y ¢ Î G, для которого верно неравенство Y ¢³Y*.Так как функция F возрастающая по отношению ³, то противоречит (10.6). Аналогично доказываются достаточные условия слабой эффективности. Теорема 5 играет важную роль в решении многокритериальных задач. Её применение основано на максимизации возрастающих функций многих переменных. Поэтому целесообразно рассмотреть примеры таких функций. 1). Функция F (Y) =
 , при s >0 и , при s >0 и  >0 является возрастающей по каждой переменной на множестве неотрицательных чисел и потому возрастает по ³ на E >= (т.е. в пространств Е где все >0 является возрастающей по каждой переменной на множестве неотрицательных чисел и потому возрастает по ³ на E >= (т.е. в пространств Е где все  >=0). Если же s<0 и >=0). Если же s<0 и  >0, то эта функция возрастает по ≥ на Е > (т.е. в области положительных >0, то эта функция возрастает по ≥ на Е > (т.е. в области положительных  ). Точка максимума такой функции эффективна. ). Точка максимума такой функции эффективна.
3).Функция F (Y)
 при при  >0 возрастает по каждой переменной >0 возрастает по каждой переменной  на множестве положительных чисел и поэтому является возрастающей по ≥ на Е > . Если же на множестве положительных чисел и поэтому является возрастающей по ≥ на Е > . Если же  ≥0 и есть среди них положительные, то эта функция будет возрастающей по отношению > на Е > . ≥0 и есть среди них положительные, то эта функция будет возрастающей по отношению > на Е > .
5). Возьмём функцию F (Y)
 и, значит, приведённая функция возрастает по отношению > на E. Следовательно, любая её точка максимума на G слабо эффективна. и, значит, приведённая функция возрастает по отношению > на E. Следовательно, любая её точка максимума на G слабо эффективна.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 Для наглядности рассуждений рассмотрим пример с двумя критериями (рис10.1). Независимо от предпочтений ЛПР, вектор критериев, соответствующий точке 2, лучше, чем в точке 1. Аналогично, точка 3 лучше точки 2, а 4 лучше 3. Но точки 4 и 5 оказываются не сравнимыми, так как по первому критерию лучше точка 5, а по второму – точка 4. Как для точки 5, так и для 4 на множестве G можно найти лучшую точку, например 6. Нетрудно убедиться в том, что для любой точки Y внутри G найдется точка, которая ее доминирует, т.е. лучше хотя бы по одному частному критерию и не хуже по всем другим. В то же время для точек 6 или 7 этого сделать нельзя. Более того, не найдется вектора из G, который доминировал бы точку, принадлежащую северо-восточной границе AB множества G. Таким образом, векторы на АВ являются недоминируемыми (неулучшаемыми). Одновременно они являются несравнимыми между собой (например, в точках 6 и 7), поэтому отдать предпочтение одному из них без ЛПР невозможно. Такие точки (векторы критериев и соответствующие решения) называют эффективными или оптимальными по Парето. Их совокупность образует множество Парето (паретовское множество).
Для наглядности рассуждений рассмотрим пример с двумя критериями (рис10.1). Независимо от предпочтений ЛПР, вектор критериев, соответствующий точке 2, лучше, чем в точке 1. Аналогично, точка 3 лучше точки 2, а 4 лучше 3. Но точки 4 и 5 оказываются не сравнимыми, так как по первому критерию лучше точка 5, а по второму – точка 4. Как для точки 5, так и для 4 на множестве G можно найти лучшую точку, например 6. Нетрудно убедиться в том, что для любой точки Y внутри G найдется точка, которая ее доминирует, т.е. лучше хотя бы по одному частному критерию и не хуже по всем другим. В то же время для точек 6 или 7 этого сделать нельзя. Более того, не найдется вектора из G, который доминировал бы точку, принадлежащую северо-восточной границе AB множества G. Таким образом, векторы на АВ являются недоминируемыми (неулучшаемыми). Одновременно они являются несравнимыми между собой (например, в точках 6 и 7), поэтому отдать предпочтение одному из них без ЛПР невозможно. Такие точки (векторы критериев и соответствующие решения) называют эффективными или оптимальными по Парето. Их совокупность образует множество Парето (паретовское множество). Однако при непрерывном и тем более невыпуклом множестве G паретовское множество имеет сложную структуру и его исследование требует специальных методов
Однако при непрерывном и тем более невыпуклом множестве G паретовское множество имеет сложную структуру и его исследование требует специальных методов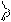

 Очевидно, что для любой пары a,b
Очевидно, что для любой пары a,b  A выполняется только одно из трех соотношений: a ý b, b ý a, a~b. Объединение P и I дает отношение нестрогого предпочтения, обозначаемого символом (a b или a R b). Отношение a b означает, что a не менее предпочтительно, чем b.
A выполняется только одно из трех соотношений: a ý b, b ý a, a~b. Объединение P и I дает отношение нестрогого предпочтения, обозначаемого символом (a b или a R b). Отношение a b означает, что a не менее предпочтительно, чем b.

 В соответствии с этими определениями решение Х *
В соответствии с этими определениями решение Х *  ,
, 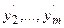 ) предпочтительнее вектора (
) предпочтительнее вектора (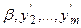 ), а вектор (
), а вектор ( ) менее предпочтителен, чем (
) менее предпочтителен, чем (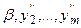 ), то какое из значение первого критерия,
), то какое из значение первого критерия,  , предпочтительнее сказать нельзя без знания значений остальных критериев. Так, например, чем выше потолок комнаты, тем лучше, но справедливо это до определенных соотношений высоты, ширины и длины комнаты. Чаще, однако, все значения частного критерия можно упорядочить по предпочтению без учета значений других критериев. Такие критерии называют независимыми по предпочтению от остальных. Примерами могут служить прибыль, издержки и т.п.
, предпочтительнее сказать нельзя без знания значений остальных критериев. Так, например, чем выше потолок комнаты, тем лучше, но справедливо это до определенных соотношений высоты, ширины и длины комнаты. Чаще, однако, все значения частного критерия можно упорядочить по предпочтению без учета значений других критериев. Такие критерии называют независимыми по предпочтению от остальных. Примерами могут служить прибыль, издержки и т.п. Y ’ (т.е. Y
Y ’ (т.е. Y  Y ’) или Y>Y ’ (т.е.
Y ’) или Y>Y ’ (т.е.  для
для  ). Наконец, равенство = порождает отношение безразличия.
). Наконец, равенство = порождает отношение безразличия.
 Поэтому, если весь угол (ортант), построенный на некоторой точке Y *
Поэтому, если весь угол (ортант), построенный на некоторой точке Y *  P(Y), т.е. не является эффективной.
P(Y), т.е. не является эффективной.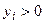 . Вектор Y * слабо эффективен тогда и только тогда, когда найдутся такие числа
. Вектор Y * слабо эффективен тогда и только тогда, когда найдутся такие числа  , что
, что (10.1)
(10.1) положительной константы
положительной константы 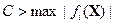 .
. , вогнуты и положительны на D. Тогда решение X * слабо эффективно в том и только в том случае, если существуют такие числа
, вогнуты и положительны на D. Тогда решение X * слабо эффективно в том и только в том случае, если существуют такие числа 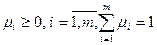 , что
, что . (10.2)
. (10.2) , при которых
, при которых . (10.3)
. (10.3) Требование вогнутости f существенно, так как его невыполнение может привести к тому, что не для всех слабо эффективных решений найдутся
Требование вогнутости f существенно, так как его невыполнение может привести к тому, что не для всех слабо эффективных решений найдутся  , удовлетворяющие (10.3). Например, для критериев
, удовлетворяющие (10.3). Например, для критериев  и
и  (
(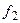 выпукла) на D =[0,1] множество S(X)= D. Максимум функции
выпукла) на D =[0,1] множество S(X)= D. Максимум функции  достигается только на одном из концов интервала [0,1] и поэтому ни при каких неотрицательных
достигается только на одном из концов интервала [0,1] и поэтому ни при каких неотрицательных  и
и  максимизация этой функции не даст слабо оптимальную точку, лежащую внутри D.
максимизация этой функции не даст слабо оптимальную точку, лежащую внутри D.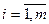
 , (10.4)
, (10.4)
 ¦
¦  >
> 
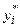 ,
,  }. (10.5)
}. (10.5) , где
, где  , является возрастающей по каждой переменной
, является возрастающей по каждой переменной  и хотя бы одном из них положительном является возрастающей по отношению > и, значит, максимизация такой функции на G дает слабо эффективную точку.
и хотя бы одном из них положительном является возрастающей по отношению > и, значит, максимизация такой функции на G дает слабо эффективную точку. , где s >0,
, где s >0, 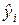 >=
>= 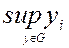 ,
,  , возрастает по ≥ на G. Поэтому любая её точка максимума на G эффективна. Отсюда, в частности, следует, что минимизация широко применяемой функции
, возрастает по ≥ на G. Поэтому любая её точка максимума на G эффективна. Отсюда, в частности, следует, что минимизация широко применяемой функции  дает эффективную точку.
дает эффективную точку. при
при  ,
,  для всех i, тои
для всех i, тои  для всех i. Поэтому справедливо неравенство
для всех i. Поэтому справедливо неравенство


