
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие базиса. Переход от одного базисного решения к другомуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Здесь нам понадобятся некоторые понятия линейной алгебры.. Векторы А 1, А 2, …, АS являются линейно-независимыми, если равенство k 1 A 1 +k 2 A 2 +…+kSAS =0 выполняется только при k 1 =k 2 =…=kS= 0. Признаком линейной независимости векторов является ненулевое значение определителя, составленного из этих векторов, так как однородная система имеет единственное (нулевое) решение только при таком определителе. Если есть система линейно-независимых векторов, то любой другой вектор может быть выражен в виде их линейной комбинации и притом единственным образом: Ap=a 1 A 1 +a 2 A 2 +…+aSAS, pÏ[1, S]. В канонической форме условия записываются в виде
Пусть система (4.4) имеет базисное решение:
Тогда из (4.4) следует
Так как система (4.6) совместна, то ее определитель не равен нулю и, значит, векторы, входящие в (4.6), являются линейно-независимыми. Для их обозначения введем следующее понятие: система m линейно-независимых векторов, соответствующих базисным переменным, называется базисом. Таким образом, каждой экстремальной точке соответствует своё базисное решение и свой базис. Теперь, имея исходные базисное решение (4.5) и базис Пусть вводимой будет переменная с индексом rÏ[1,m], принимающая в новом решении некоторое положительное значение В новом решении, как в любом допустимом, условия (4.4) также должны выполняться, поэтому имеем:
Задача состоит в том, чтобы определить X (1) по X( 0). С этой целью сделаем несложные преобразования. Выразим вектор Ar через исходный базис: Ar=A 1 a 1 r+A 2 a 2 r+…+Amamr .(4.8) Так как известен базис, то известны (или находятся решением этой ситстемы) коэффициенты разложения air. Умножим левую и правую части равенства (4.8) на q: qAr=qA 1 a 1 r +qA 2 a 2 r +…+qAmamr. (4.9) Вычитая (4.9) из (4.6), получим:
или окончательно:
Сравнивая равенства (4.7) и (4.10), видим, что правые части равны, а левые содержат одну и ту же ситстему векторов. Поэтому коэффициенты при одноименных векторах должны совпадать. Приравнивая их, получаем искомые соотношения:
Однако решение (4.11) может быть недопустимым, если не оговорить возможные значения q. Предположим, что среди коэффициентов air есть положительные. Тогда с увеличением значения q соответствующие переменные могут стать отрицательными. Поэтому для допустимости решения X (1) необходимо, чтобы q было ограничено сверху:
С учетом (4.12) решение (4.11) всегда будет допустимым, но число ненулевых переменных в нем может превышать m, так как добавлена xr , а значит, оно может быть небазисным. Если же в качестве значения q выбрать q0, то одна из переменных Пусть минимум в (4.12) достигается на переменной xk. Тогда базисные переменные в новом опорном решении будут вычисляться по формулам:
Этому решению соответствует новый базис {Ai}(1)={A 1 ,…,Ak- 1 ,Ar, Ak+ 1 ,…,Am}. Таким образом, переход к новому базисному решению произошел путем замены переменной Xk на Xr, соответсвенно в базисе - Ak на Ar.
При вычислении q0 минимум может достигаться более чем на одном индексе. При этом обнуляется более одной переменной из входящих в исходное решение. Следовательно, в новом решении будут базисные переменные с нулевым значением, что означает попадание в вырожденное базисное решение. Если исходное решение вырожденное и нулевой переменной соответствует коэффициет akr >0, то согласно (4.12) q0 =0 и значения переменных не изменяются. Однако состав базиса и базисных переменных изменится - произойдет замена
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 (4.4)
(4.4) (4.5)
(4.5) (4.6)
(4.6) , построим новое базисное решение. Как следует из геометрических представлений, смежные вершины отличаются по составу базисных переменных только одной. Поэтому новое решение можно получить вводом в исходное небазисной переменной с одновременным переводом одной базисной переменной в небазисные.
, построим новое базисное решение. Как следует из геометрических представлений, смежные вершины отличаются по составу базисных переменных только одной. Поэтому новое решение можно получить вводом в исходное небазисной переменной с одновременным переводом одной базисной переменной в небазисные.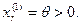
 (4.7)
(4.7)
 (4.10)
(4.10) (4.11)
(4.11) (4.12)
(4.12) станет равной нулю, а решение (4.11) - базисным.
станет равной нулю, а решение (4.11) - базисным. (4.13)
(4.13)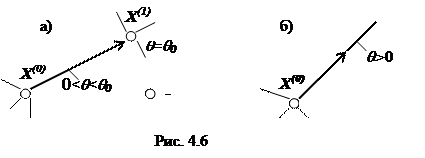 Рассмотрим возможные ситуации при переходе от одного решения к другому. Как было показано выше, при существовании положительных коэффициентов air достигается новое базисное решение (смежная вершина), что иллюстрируется рис. 4.6-а. Если же все air неположительны, величина q, а это значениевводимой переменной, не ограничена сверху. Следовательно, введение такой переменной не приведет к получению базисного решения (достижению новой вершины). Это признак того, что соответствующее ребро допустимого множества, а значит, и само множество оказываются неогранниченными (рис. 4.6-б).
Рассмотрим возможные ситуации при переходе от одного решения к другому. Как было показано выше, при существовании положительных коэффициентов air достигается новое базисное решение (смежная вершина), что иллюстрируется рис. 4.6-а. Если же все air неположительны, величина q, а это значениевводимой переменной, не ограничена сверху. Следовательно, введение такой переменной не приведет к получению базисного решения (достижению новой вершины). Это признак того, что соответствующее ребро допустимого множества, а значит, и само множество оказываются неогранниченными (рис. 4.6-б).
 на
на  При высокой степени вырожденности теоретически возможно зацикливание, то есть возврат к старому базису, но на практике такие случаи не встречались.
При высокой степени вырожденности теоретически возможно зацикливание, то есть возврат к старому базису, но на практике такие случаи не встречались.


