
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 11. Задачи линейного программированияСодержание книги Поиск на нашем сайте
56. Решите задачу линейного программирования графическим способом:
57. Решите задачу симплекс-методом:
58. Решите задачу симплекс-методом:
59. Предприятие выпускает два вида продукции П1 и П2. Для выпуска каждого вида продукции требуется 4 вида ресурсов: Р1, Р2, Р3, Р4. Объем ресурсов вида Требуется: а) решить задачу графическим методом; б) решить задачу симплексным методом, поставить двойственную задачу, найти ее решение и проверить правильность решения прямой и двойственной задачи с помощью теоремы двойственности; в) дать экономическую интерпретацию решений прямой и двойственной задач.
60. При откорме животных каждое животное ежедневно должно получить не менее 60 ед. питательного вещества А, не менее 50 ед. питательного вещества В и не менее 12 ед. вещества С. Указанные питательные вещества содержат три вида корма. Содержание единиц питательных веществ в 1кг каждого из видов корма приведено в таблице:
Составьте дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах, если цена 1 кг корма 1 вида составляет 9 руб., корма 2 вида – 12 руб., корма 3 вида – 10 руб. 61. На трех складах оптовой базы сосредоточен однородный груз в количествах 90, 60 и 150 ед. Этот груз необходимо перевезти в 4 магазина. Каждый из магазинов должен получить соответственно 120, 40, 60 и 80 ед. груза. Тарифы перевозок ед. груза из каждого из складов во все магазины задаются матрицей:
Составьте такой план перевозок, при котором общая стоимость перевозок является минимальной. Начальный план перевозок транспортной задачи построить методом северо-западного угла.
62. Производственное объединение имеет в своем составе три филиала, которые производят однородную продукцию соответственно в количествах, равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя, расположенные в разных местах. Их потребности соответственно равны 30, 30, 10 и 20 ед. Тарифы перевозок ед. продукции от каждого из филиалов соответствующим потребителям задаются матрицей:
Составьте такой план прикрепления получателей продукции к ее поставщикам, при котором общая стоимость перевозок будет минимальной. Начальный план прикрепления получателей продукции к ее поставщикам построить методом наименьшей стоимости. 63. Некоторый однородный груз, сосредоточенный у четырех поставщиков А1,А2,А3,А4 в количестве а1,а2,а3,а4 единиц соответственно, необходимо доставить пяти потребителям В1,В2,В3,В4,В5 в количестве b1, b 2, b 3, b 4, b 5 ед. соответственно. Тарифы
а1=24,а2=32,а3=43,а4=16; b1=20, b 2=45, b 3=10, b 4=15, b 5=25. Раздел IY. Теория вероятностей и математическая статистика
Тема 12. Основные понятия и теоремы теории вероятностей 64. На каждой из шести одинаковых карточек напечатана одна из букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найдите вероятность того, что на четырех, вынутых по одной и расположенных “в одну линию” карточках, можно будет прочесть слово «сорт». 65. Набирая номер телефона, абонент не помня одну цифру, набрал ее наудачу. Найдите вероятность того, что набрана нужная цифра. 66. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найдите вероятность того, что набраны нужные цифры. 67. В партии из 10 изделий 7 стандартных. Найдите вероятность того, что среди шести взятых наудачу деталей 4 стандартных. 68. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найдите вероятность того, что среди извлеченных деталей а) нет бракованных; б) нет годных. 69. Есть 3 билета в различные театры. Сколькими способами они могут быть распределены среди 25 студентов группы, если каждый студент может получить только один билет?
70. На группу из 25 человек выделены 3 пригласительных билета на вечер. Сколькими способами они могут быть распределены (не более одного билета в руки)?
71. В группе из 15 человек 7 студентов не выполнили домашнего задания по математике. Преподаватель опрашивает 5 человек. Найдите вероятность того, что преподаватель вызовет 2 человека из числа не выполнивших домашнего задания. 72. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найдите вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие. 73. В урне 30 шаров: 10 красных, 5 синих, 15 белых. Найдите вероятность появления цветного шара (не белого). 74. Вероятности попадания в цель при стрельбе из трех орудий таковы: р1=0,8; р2=0,7; р3=0,9. Найдите вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. 75. В урне 5 белых, 4 черных, 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найдите вероятность того, что при первом испытании появится белый шар (событие А), при втором – черный (событие В), при третьем – синий (событие С). 76. В урну, содержащую 2 шара, опущен белый шар, после чего из него наудачу извлечен один шар. Найдите вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету). 77. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найдите вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная. 78. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найдите вероятность того, что эта деталь произведена первым автоматом. 79. Детали, изготовленные цехом завода, попадают для проверки их на стандартность к одному из контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найдите вероятность того, что эту деталь проверил первый контролер. 80. Монету бросают 5 раз. Найдите вероятность того, что «герб» выпадет: а) менее 2 раз; б) не менее 2 раз. 81. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найдите вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы. 82. В семье 5 детей. Найдите вероятность того, что среди этих детей: а) 2 мальчика; б) не более 2 мальчиков; в) более 2 мальчиков; г) не менее 2 и не более 3 мальчиков. Вероятность рождения мальчика принять равной 0,51. 83. Найдите вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25. 84. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,8. Найдите вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз;
б) не менее 75 раз; в) не более 75 раз.
Тема 13. Случайные величины 85. Дискретная случайная величина Х задана законом распределения:
Постройте многоугольник распределения. 86. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составьте закон распределения числа отказавших элементов в одном опыте. 87. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны 2 детали. Составьте закон распределения числа отказавших элементов в одном опыте. 88. В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Напишите биномиальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и постройте многоугольник полученного распределения. 89. Найдите математическое ожидание дискретной случайной величины Х, заданной законом распределения:
90. Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения:
91. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найдите вероятность того, что за 2 минуты поступит: а) 4 вызова; б) менее 4 вызовов; в) не менее 4 вызовов. 92. Найдите математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, распределенной по закону Пуассона:
93. Случайная величина Х задана интегральной функцией:
Найдите вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0; 1/3). 94. Случайная величина Х задана интегральной функцией:
Найдите вероятность того, что в результате испытания величина Х примет значение: а) меньшее 0,2; б) меньшее 3; в) не меньшее 3; г)не меньшее 5. 95. Случайная величина Х задана дифференциальной функцией f(x)=2x в интервале (0;1); вне этого интервала f(x)=0. Найдите математическое ожидание величины Х. 96. Найдите математическое ожидание случайной величины Х, заданной интегральной функцией:
97. Случайная величина Х задана дифференциальной функцией f(x)=1/2 sinx в интервале (0;π); вне этого интервала f(x)=0. Найдите дисперсию величины Х. 98. Найти дисперсию случайной величины Х, заданной интегральной функцией:
99. Найдите математическое ожидание и дисперсию случайной величины Х, распределенной равномерно в интервале (a, b).
100. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратичное отклонение этой величины соответственно равны 30 и 10. Найдите вероятность того, что Х примет значение, принадлежащее интервалу (10, 50). 101 Непрерывная случайная величина Х распределена по показательному закону. Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,3; 1). 102. Вероятность появления события А в каждом испытании равна ½. Используя неравенство Чебышева, оцените вероятность того, что число Х появлений события А заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.
103. Последовательность независимых случайных величин Х1, Х2,…,Хп задана законом распределения:
Применима ли к данной последовательности теорема Чебышева? 104. Задана матрица перехода системы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.212.244 (0.008 с.) |







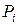 , которыми располагает предприятие, равен
, которыми располагает предприятие, равен 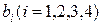 . Цена 1 единицы продукции вида Пj равна Сj (j = 1,2). Объемы ресурсов каждого вида
. Цена 1 единицы продукции вида Пj равна Сj (j = 1,2). Объемы ресурсов каждого вида 
 .
.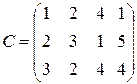
 c
c  перевозок 1 ед. груза от I-го поставщика к j-му производителю заданы матрицей С. Требуется составить план перевозок, имеющий минимальную стоимость, позволяющий вывезти все грузы и удовлетворить все потребности потребителей.
перевозок 1 ед. груза от I-го поставщика к j-му производителю заданы матрицей С. Требуется составить план перевозок, имеющий минимальную стоимость, позволяющий вывезти все грузы и удовлетворить все потребности потребителей.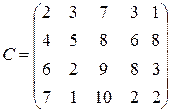 ;
;
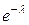
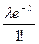
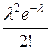


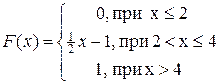

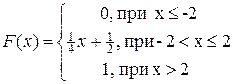
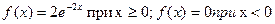
 . Найдите матрицу перехода Р2, Р3.
. Найдите матрицу перехода Р2, Р3.


