
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 10. Классические методы оптимизацииСодержание книги Поиск на нашем сайте Классическая задача на условный экстремум - специфическая задача для функции нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию, которое называется уравнением связи. Наиболее простым способом нахождения условного экстремума функции двух переменных Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Тема 11. Задачи линейного программирования Задача линейного программирования сводится к следующему: требуется найти некоторую совокупность переменных, удовлетворяющих системе ограничений в форме равенств и неравенств минимизирующих (максимизирующих) линейную функцию. Если положительным компонентам некоторого допустимого решения отвечают линейно независимые векторы условий, то это допустимое решение является вершиной многоугольника решений. В теории линейного программирования по симплекс-методу осуществляется целенаправленный перебор соседних вершин многоугольника решений так, чтобы в новой вершине значение функции цели было меньше, тогда за конечное число итераций будет получено решение задачи. Среди задач линейного программирования встречаются задачи, допускающие решение более простыми методами. К таким относится транспортная задача. Она заключается в следующем: требуется составить план перевозок однородного груза из пунктов отправления, в каждом из которых имеется определенное количество единиц груза, в пункты назначения с целью удовлетворения запросов всех потребителей и минимизировать суммарную стоимость перевозок. Раздел IY. Теория вероятностей и математическая статистика Тема 12. Основные понятия и теоремы теории вероятностей Приступая к изучению этого раздела, студентам необходимо познакомится с основными понятиями теории вероятностей к которым можно отнести: испытание и случайное событие, частота и относительная частота появления события в серии испытаний, свойство устойчивости относительной частоты, статистическое и классическое определения вероятности. Студент должен знать простейшие свойства вероятности. Не всегда возможно вычисление вероятности какого-либо события с использованием только классического определения вероятности. В некоторых задачах вероятности отдельных "исходных" событий известны и требуется вычислить вероятность другого события, являющегося комбинацией исходных. В таких задачах используют теоремы сложения и умножения вероятностей. Если требуется вычислить вероятность события при условии, что известны значения его вероятности при выполнении некоторых гипотез, или требуется переоценить значения вероятностей гипотез с учетом некоторой дополнительной информации о результатах испытания, то для решения такого рода задач используются формулы полной вероятности и формулы Байеса. Студенты должны знать определения, теоремы, формулы вычисления вероятностей и условия их применимости к той или иной задаче. При осуществлении серии из п однородных независимых испытаний, в каждом из которых может произойти или не произойти некоторое событие А и требуется определить вероятность того, что в этой серии испытаний событие А произойдет определенное число раз, или вероятность того, что количество появлений события А в данной серии испытаний будет заключено в определенных границах используется: 1) если число испытаний п невелико и требуется вычислить вероятность того, что событие А в данной серии испытаний произойдет ровно k раз, т.е. 2) если число испытаний велико, для вычисления вероятности
Тема 13. Случайные величины Целью изучения данной темы является усвоение студентами таких понятий, как случайная величина, дискретная случайная величина, закон распределения случайной величины. Понятие случайной величины определяется следующим образом. Осуществляется некоторое испытание, для которого известна совокупность элементарных исходов. В связи с данным испытанием рассматривается некоторая величина, которая в результате испытания может принимать различные числовые значения, не поддающиеся прогнозированию. Однако, известно, что при каждом конкретном элементарном исходе испытания эта величина принимает одно определенное значение. Эта величина называется случайной. Если множество возможных значений случайной величины конечно или бесконечно и может быть записано в виде последовательности, то такая случайная величина называется дискретной. Законом распределения дискретной случайной величины называется соответствие между всеми возможными значениями этой случайной величины и вероятностями, с которыми данная случайная величина принимает эти значения. Закон распределения дискретной случайной величины может быть задан таблицей, формулой, графиком. Студенты должны знать определения, понимать эмпирический смысл числовых характеристик дискретных случайных величин (математическое ожидание, дисперсия, среднее квадратическое отклонение). Конкретным примером закона распределения дискретной случайной величины является биномиальный закон распределения. Студентам необходимо знать определение биномиального закона, его связь с формулой Бернулли и числовые характеристики случайной величины, распределенной по биномиальному закону. Необходимо знать распределение Пуассона. При изучении непрерывных случайных величин необходимо усвоить: случайная величина Х называется непрерывной случайной величиной, если закон ее распределения может быть задан равенством Студенты должны знать определения и свойства функции распределения и плотности вероятности случайной величины, взаимосвязь функции распределения и плотности вероятности, знать определения и понимать эмпирический смысл числовых характеристик непрерывной случайной величины (математическое ожидание, дисперсия, среднее квадратическое отклонение). В качестве примеров законов распределения непрерывных случайных величин необходимо рассматривать конкретные законы распределения (равномерный, нормальный, показательный). Студентам необходимо знать определения законов распределения, числовые характеристики, формулы для вычисления вероятности попадания случайной величины в заданный интервал. Закон больших чисел устанавливает близость между вероятностью случайного события и частостью появления его при большом числе испытаний. Наиболее общая форма этого закона дана П.Л. Чебышевым. Теорема Чебышева имеет применение в теории ошибок наблюдений.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.28.79 (0.006 с.) |

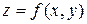 является сведение задачи к отысканию экстремума функции одной переменной. Данный способ приемлем, когда уравнение связи представляет собой достаточно простую функцию, например линейную.
является сведение задачи к отысканию экстремума функции одной переменной. Данный способ приемлем, когда уравнение связи представляет собой достаточно простую функцию, например линейную.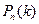 , формула Бернулли. Вероятность
, формула Бернулли. Вероятность 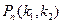 того, что в данной серии испытаний событие А произойдет не менее k1 раз и не более k2 раз вычисляется с помощью формулы Бернулли и теоремы сложения вероятностей;
того, что в данной серии испытаний событие А произойдет не менее k1 раз и не более k2 раз вычисляется с помощью формулы Бернулли и теоремы сложения вероятностей;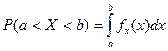 , где (
, где (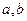 ) – произвольный интервал числовой оси,
) – произвольный интервал числовой оси,  - плотность вероятности случайной величины Х.
- плотность вероятности случайной величины Х.


