
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение транспортной задачи с помощью средства MS Excel «Поиск решения»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте УТВЕРЖДАЮ
Директор КФ СПб ГУП ________________/В.К. Подлесский/ подпись расшифровка подписи “___” ____________________ 2014г.
Методы оптимальных решений. Часть 2 Методические указания и задания для контрольных работ Направление: Экономика Форма обучения: заочная Кафедра ЕСТЕСТВЕННО-НАУЧНЫХ ДИСЦИПЛИН
Красноярск 2014
Методы оптимальных решений. Часть 2. Методические указания и задания для контрольных работ для студентов направления Экономика Божков А.Р. – Красноярск: СПб ГУП (Красноярский филиал), 2014. – 13 с. Составитель: к.ф.-м.н. Божков А.Р.
Транспортная задача Постановки задачи
Транспортная задача является одной из наиболее распространенных задач линейного программирования и находит широкое практическое приложение. Постановка транспортной задачи. Некоторый однородный продукт, сосредоточенный у т поставщиков Ai, в количестве ai (i = 1,..., т)единиц, необходимо доставить n потребителям Bj в количестве bj (j = 1, ..., п)единиц. Известна стоимость Cij перевозки единицы груза от i -го поставщика к j -му потребителю. Необходимо составить план перевозок, позволяющий вывести все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость. Сформулируем экономико-математическую модель транспортной задачи. Обозначим через Xij количество единиц груза, запланированных к перевозке от i -го поставщика к j -му потребителю. Так как от i -ro поставщика к j -му потребителю запланировано к перевозке xij единиц груза, то стоимость перевозки составит CijXij. Стоимость всего плана выразится двойной суммой
Систему ограничений получаем из следующих условий задачи: а) все грузы должны быть перевезены, т.е.
б) все потребности должны быть удовлетворены, т.е.
Таким образом, математическая модель транспортной задачи имеет следующий вид: найти минимальное значение линейной функции
при ограничениях
Видно, что эта модель является частным случаем задачи линейного программирования. Кроме того, предположим, что имеет место баланс производства-потребления:
Транспортная задача имеет п + т уравнений с т x п неизвестными. Матрицу X= (Xij) mn , удовлетворяющую условиям (2)–(4), называют планом перевозок транспортной задачи, а Xij называются перевозками. План X*, при котором целевая функция (1) обращается в минимум, называется оптимальным. Следует отметить, что m+n ограничений (3) – (4) линейно зависимы и одним из них можно пренебречь. Соответственно, опорный план транспортной задачи может содержать не более m+n–1 положительных компонент. Опорные планы, в которых положительных составляющих меньше m+n–1, называются вырожденными. Вычислить решение задачи. В результате получено решение
x 13 = 80 ед. груза следует перевезти от 1-го поставщика 3-му потребителю; x 21 = 200 ед. груза следует перевезти от 2-го поставщика 1-му потребителю; x 23 = 70 ед. груза следует перевезти от 2-го поставщика 3-му потребителю; x 24 = 50 ед. груза следует перевезти от 2-го поставщика 4-му потребителю; x 32 = 100 ед. груза следует перевезти от 3-го поставщика 2-му потребителю; x 41 = 50 ед. груза следует перевезти от 4-го поставщика 1-му потребителю; x 42 = 0 ед. груза следует перевезти от 4-го поставщика 2-му потребителю.
Общая стоимость перевозок = 3200.
Метод множителей Лагранжа Рассмотрим теперь задачи условной оптимизации, то есть когда в задаче на определение экстремума функции множество допустимых решений
где gi и hj называются функциями ограничения. Если среди всех функций f, gi, hj имеется хотя бы одна нелинейная функция, то (7.1) называется задачей нелинейного программирования. В противном случае это есть задача линейного программирования. Если все эти функции дифференцируемы в Rn, то (7.1) называется гладкой задачей нелинейного программирования. Будем считать, что задача (7.1) гладкая и составим для нее так называемую функцию Лагранжа, зависящую от n+k+m переменных
где В формулировке необходимых признаков будет применяться градиент функции L по x:
. Теорема (необходимое условие Куна-Таккера). Пусть задача (7.1) гладкая. Для того, чтобы точка 1. условия стационарности:
2. условия дополняющей нежесткости:
3. условия неотрицательности:
причем все множители Лагранжа С помощью условий этой теоремы можно составить следующий алгоритм решения задачи (7.1), который называется методом множителей Лагранжа: 1. убедиться в существовании экстремальных точек (теорема Вейерштрасса и ее следствие); 2. составить функцию Лагранжа (7.2); 3. выписать все необходимые условия (7.3)-(7.5); 4. вычислить все стационарные точки, то есть найти все решения уравнений (7.3); 5. определить характер экстремума стационарных точек. Рассмотрим более простую формулировку задачи на условный экстремум.
для решения которых можно воспользоваться классическим методом оптимизации Лагранжа, или методом разрешающих множителей. При этом предполагают, что функции Можно указать следующий порядок решения задачи (7.6)-(7.7) методом множителей Лагранжа: 1) составить функцию Лагранжа:
здесь 2) Найти частные производные функции Лагранжа по всем переменным
Эта система состоит из m + n уравнений. Решить эту систему (если это окажется возможным) и найти таким образом все стационарные точки функции Лагранжа; 3) из стационарных точек, взятых без координат В основе метода Лагранжа решения классической задачи оптимизации (7.6)-(7.7) лежит утверждение, что если Множителям Лагранжа можно придать следующий экономический смысл. Если Пример 7.1. По плану производства продукции предприятию необходимо изготовить 200 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. Производственные затраты на изготовление n изделий первым способом равны 4 n+n2, а для второго способа - 8 n+n2. Сколько изделий надо изготовить каждым способом, чтобы общие затраты на производство продукции были бы минимальными. Решение. Обозначим число изделий, изготовленных первым способом через х1, вторым способом – х2 . Тогда суммарные затраты на изготовление продукции по плану составят: f (x1,x2)=4x1+x12+8x2+x22 При этом общее число изделий должно быть равно 200, т.е. x1+ x2 =200 Получим математическую модель задачи: f (x1,x2)=4x1+x12+8x2+x22 → min x1+ x2 =200 x1 ≥ 0, x2 ≥ 0 Для ее расчета применим метод множителей Лагранжа. Составим функцию Лагранжа L(x1,x2,λ)=4x1+x12+8x2+x22+ λ (200-x1-x2) Найдем частные производные функции L по x1, x2, λ и приравняем их к нулю:
имеем систему:
Исключим из этой системы λ, например, выразим λ из первого уравнения
Таким образом, по необходимому условию экстремума дифференцируемой функции получим стационарную точку X(101,99) возможного условного экстремума функции f(x1,x2). Дальнейшее исследование этой точки будем проводить, как и в случае безусловного экстремума. Вспомним сначала достаточные условия существования локального экстремума для случая функции двух переменных z = f(x, y. Обозначим вторые частные производные этой функции ТЕОРЕМА. Пусть в точке М 0 (х 0, у 0 ) возможного экстремума функции z = f(x, у) и в некоторой ее окрестности все вторые частные производные этой функции непрерывны. Тогда если
то функция z = f(x, у) имеет в точке М 0 локальный экстремум: минимум при а 11 > 0 и максимум при а 11 < 0. Если же а 11 а 22 — a 122 ≤ 0, то данная функция не имеет локального экстремума в точке M 0. В данном примере найдем частные производные второго порядка:
Проверим условие Так a 11= 2 >0, то в точке X(101,99) функция f(x1,x2) имеет минимум:
Ответ. При изготовлении 101 детали первым способом и 99 деталей вторым способом затраты на производство будут минимальными и равными 21198 денежным единицам.
Задания для самостоятельной работы. Задание 1. Решение транспортной задачи Формулировка задачи. Имеются три пункта производства, располагающие некоторым однородным продуктом в количествах a1, a2 и a3. Продукт необходимо доставить в пять пунктов конечного потребления, платежеспособный спрос в которых составляет b1, b2, b3, b4 и b5. Затраты на транспортировку (прямую поставку) единицы продукта от пункта производства в пункт потребления приведены в таблице С, расположенной в таблице 1 Требуется отыскать такие объемы прямых поставок продукта от пунктов производства к пунктам потребления, при которых достигается минимум суммарных транспортных затрат. Информацию о задаче соответствующую вашему варианту возьмите из таблицы 1. Таблица 1
Задание 2. Нелинейные задачи условной оптимизации
Задача 1. По плану производства продукции предприятию необходимо изготовить d изделий. Эти изделия могут быть изготовлены двумя технологическими способами. Производственные затраты на изготовление n изделий первым способом равны Таблица
Задача 2. Фирма реализует товар двумя способами: через магазин и через торговых агентов. При реализации товара в количестве x единиц через магазин расходы на реализацию составляют R1(x), а при продаже товара в количестве y единиц через торговых агентов расходы составляют R2(y). Требуется, используя принцип Лагранжа, составить план реализации товара, минимизирующий общие расходы, если R1(x) = x 2 – k x +400, R2(y) = y 2 – m y +25 и общее число предназначенных для продажи товаров составляет 63 единицы.
Таблица
Литература 1. Соловьев В. И. Методы оптимальных решений: Учебное пособие. М.: Финансовый Университет, 2012. 364 с. 2. Окунева Е.О., Моисеев С.И.. Методы оптимальных решений –Воронеж: ВФ МГЭИ, 2013. – 139 с. 3. Конюховский П. В. Математические методы исследования операций в экономике. — СПб: Питер, 2000.—208 с 4. Математические методы моделирования экономических систем/ Е.В. Бережная, В.И. Бережной. —М.: Финансы и статистика, 2006. – 432 с. УТВЕРЖДАЮ
Директор КФ СПб ГУП ________________/В.К. Подлесский/ подпись расшифровка подписи “___” ____________________ 2014г.
Методы оптимальных решений. Часть 2 Методические указания и задания для контрольных работ Направление: Экономика Форма обучения: заочная Кафедра ЕСТЕСТВЕННО-НАУЧНЫХ ДИСЦИПЛИН
Красноярск 2014
Методы оптимальных решений. Часть 2. Методические указания и задания для контрольных работ для студентов направления Экономика Божков А.Р. – Красноярск: СПб ГУП (Красноярский филиал), 2014. – 13 с. Составитель: к.ф.-м.н. Божков А.Р.
Транспортная задача Постановки задачи
Транспортная задача является одной из наиболее распространенных задач линейного программирования и находит широкое практическое приложение. Постановка транспортной задачи. Некоторый однородный продукт, сосредоточенный у т поставщиков Ai, в количестве ai (i = 1,..., т)единиц, необходимо доставить n потребителям Bj в количестве bj (j = 1, ..., п)единиц. Известна стоимость Cij перевозки единицы груза от i -го поставщика к j -му потребителю. Необходимо составить план перевозок, позволяющий вывести все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость. Сформулируем экономико-математическую модель транспортной задачи. Обозначим через Xij количество единиц груза, запланированных к перевозке от i -го поставщика к j -му потребителю. Так как от i -ro поставщика к j -му потребителю запланировано к перевозке xij единиц груза, то стоимость перевозки составит CijXij. Стоимость всего плана выразится двойной суммой
Систему ограничений получаем из следующих условий задачи: а) все грузы должны быть перевезены, т.е.
б) все потребности должны быть удовлетворены, т.е.
Таким образом, математическая модель транспортной задачи имеет следующий вид: найти минимальное значение линейной функции
при ограничениях
Видно, что эта модель является частным случаем задачи линейного программирования. Кроме того, предположим, что имеет место баланс производства-потребления:
Транспортная задача имеет п + т уравнений с т x п неизвестными. Матрицу X= (Xij) mn , удовлетворяющую условиям (2)–(4), называют планом перевозок транспортной задачи, а Xij называются перевозками. План X*, при котором целевая функция (1) обращается в минимум, называется оптимальным. Следует отметить, что m+n ограничений (3) – (4) линейно зависимы и одним из них можно пренебречь. Соответственно, опорный план транспортной задачи может содержать не более m+n–1 положительных компонент. Опорные планы, в которых положительных составляющих меньше m+n–1, называются вырожденными. Решение транспортной задачи с помощью средства MS Excel «Поиск решения»
В следующей таблице приведены исходные данные транспортной задачи: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза (c ij), справа указаны мощности поставщиков (a i), a снизу – мощности потребителей (b j). Найти оптимальный план закрепления поставщиков за потребителями (x ij).
В данной задаче суммарные запасы равны суммарным потребностям
т.е. данная транспортная задача является закрытой. Ввод условий задачи состоит из следующих основных шагов: 1. Создание формы для ввода условий задачи. 2. Ввод исходных данных. 3. Назначение целевой функции. 4. Ввод зависимостей из математической модели. 5. Ввод ограничений и граничных условий. 6. Ввести параметры для решения задачи. 7. Вычислить решение задачи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 718; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |




 (4)
(4)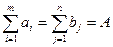 (5)
(5)
 задается с помощью системы неравенств и уравнений:
задается с помощью системы неравенств и уравнений:
 :
: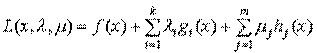
 - вектор множителей Лагранжа для ограничений- неравенств, а
- вектор множителей Лагранжа для ограничений- неравенств, а  - вектор множителя Лагранжа для ограничений-равенств.
- вектор множителя Лагранжа для ограничений-равенств.
 была точкой локального минимума (максимума) в задаче (7.1) необходимо выполнение следующих условий:
была точкой локального минимума (максимума) в задаче (7.1) необходимо выполнение следующих условий:
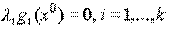

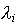 и
и  одновременно не могут быть равны нулю.
одновременно не могут быть равны нулю. (7.6)
(7.6) , (7.7)
, (7.7) и
и  непрерывны вместе со своими первыми частными производными.
непрерывны вместе со своими первыми частными производными. (7.8)
(7.8) - множители Лагранжа;
- множители Лагранжа; и приравнять их нулю. Тем самым получим систему:
и приравнять их нулю. Тем самым получим систему: (7.9)
(7.9) выбрать точки, в которых функция f(
выбрать точки, в которых функция f( имеет условные локальные экстремумы при наличии ограничений (7.7). Этот выбор осуществляется, например, с применением достаточных условий локального экстремума. Часто исследование упрощается, если использовать конкретные условия задачи.
имеет условные локальные экстремумы при наличии ограничений (7.7). Этот выбор осуществляется, например, с применением достаточных условий локального экстремума. Часто исследование упрощается, если использовать конкретные условия задачи. в точке
в точке  имеет экстремум, то существует такой вектор
имеет экстремум, то существует такой вектор 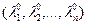 , что точка
, что точка 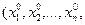
 является решением системы (6.13). Следовательно, решая систему (7.9), получаем множество стационарных точек, в которых функция f может иметь экстремальные значения. При этом, как правило, неизвестен способ определения точек глобального максимума или минимума. Однако, если решения системы найдены, то для определения глобального экстремума достаточно найти значения функции в соответствующих точках области определения.
является решением системы (6.13). Следовательно, решая систему (7.9), получаем множество стационарных точек, в которых функция f может иметь экстремальные значения. При этом, как правило, неизвестен способ определения точек глобального максимума или минимума. Однако, если решения системы найдены, то для определения глобального экстремума достаточно найти значения функции в соответствующих точках области определения. - доход, соответствующий плану
- доход, соответствующий плану  , а функция
, а функция  - издержки i -го ресурса, соответствующие этому плану, то
- издержки i -го ресурса, соответствующие этому плану, то  - цена (оценка) i -го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i -го ресурса.
- цена (оценка) i -го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i -го ресурса.

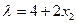 и подставим найденное значение во второе уравнение системы, получим:
и подставим найденное значение во второе уравнение системы, получим: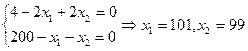
 ,
, 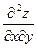 ,
,  в некоторой точке M 0 через а 11, a 12, a 22 соответственно. Тогда достаточное условие локального экстремума формулируется следующим образом.
в некоторой точке M 0 через а 11, a 12, a 22 соответственно. Тогда достаточное условие локального экстремума формулируется следующим образом.

 a11 a22 – (a12)2 = 4 >0.
a11 a22 – (a12)2 = 4 >0.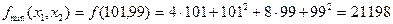 (ед.)
(ед.) , а для второго способа
, а для второго способа  . Сколько изделий надо изготовить каждым способом, чтобы общие затраты на производство продукции были бы минимальными? Исходные данные приведены в таблице.
. Сколько изделий надо изготовить каждым способом, чтобы общие затраты на производство продукции были бы минимальными? Исходные данные приведены в таблице.



