
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача оптимального управления с непрерывным временемСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим задачу о запуске ракеты с поверхности земли до высоты, которую ракета должна достичь за время Т. Обозначим через y (t) высоту, достигнутую ракетой за время t, а через u(t) – силу действующую на ракету в вертикальном направлении в момент t. Пусть масса ракеты равна m. Тогда уравнение движения имеет вид:
где g – ускорение свободного падения.
Будем считать, что максимальная сила, прилагаемая к ракете в любой момент, не превосходит b. Требуется вычислить минимальную энергию, которую необходимо затратить для выведения ракеты на высоту Эта задача может быть сформулирована следующим образом: при условиях:
Уравнение
Таким образом, задача (1.70) принимает вид:
при условиях:
Разделим отрезок [0,T] на K интервалов длины D. Чтобы упростить запись, будем считать, что D = 1. Обозначим силу, действующую на ракету, высоту полета над поверхностью и скорость ракеты в конце k -го периода соответственно через uk, y1k, y2k. Тогда задача оптимального управления полетом ракеты можно аппроксимировать следующей задачей нелинейного программирования:
при условиях: Несмотря на простоту данного примера наглядно видны принципы и приемы сведения задач оптимального управления к задачам математического программирования.
Пример 1.10. Целочисленные модели Задача о размещении Рассмотрим какую-нибудь отрасль промышленности, выпускающую товары широкого потребления, которые прямо с заводов отправляются в торговые предприятия. Требуется ответить на вопрос, где разместить каждое из промышленных предприятий и каковы должны быть их производственные мощности. При этом известно местонахождение каждой торговой точки, занимающейся розничной продажей товаров данной отрасли промышленности и известны потребности каждой из этих точек. Пусть b1,b2,..., bn, – объемы продукции, необходимые для покрытия потребностей «п» имеющихся торговых точек, a1,a2,..., am – производственные мощности «т» заводов, о размещении которых идет речь. Допустим, что известна стоимость каждого из заводов: стоимость строительства i - го завода обозначим через fi. Расходы на доставку единицы продукции от i -го завода до j -ой торговой точки равны ci j. Предположим, что i -м заводом j - й торговой точке поставляется xi j единиц продукции. Введем переменную yi, такую, что
yi = 1, если i - й завод решено построить; yi = 0, если i - й завод решено не строить. Задача заключается в том, чтобы минимизировать сумму расходов на строительство заводов и доставку товара торговым точкам при полном удовлетворении спроса потребителей.
Математическая модель задачи выглядит следующим образом:
при условиях: Если было бы заранее известно, какие заводы и где решено построить, все свелось бы к решению обычной транспортной задачи (пример 1.8). Задача о водопроводчике
Водопроводчик получил наряд на установку вентилей на нескольких трубах, проложенных под землей, покрытой тяжелыми квадратными плитами (рис. 1.3). Он может установить механизмы перекрытия в любом месте трубы, но, разумеется, лишь по одному шлюзовому затвору на каждой трубе. Для минимизации трудозатрат водопроводчику надо определить минимальное число плит, которые требуется приподнять, чтобы установить по одному затвору на каждой трубе. Пронумеруем плиты от 1 до 12. Пусть x i = 0, если выбранное решение состоит в том, чтобы не приподнимать i - ю плиту, x i = 1, если принимается решение приподнять i - ю плиту (
Математическая модель задачи выглядит следующим образом:
при условиях:
Эта задача попадает в класс так называемых задач о «покрытии множества», для которого характерны разнообразные практические приложения.
Рис 1.3
Пример 1.11. Стохастические модели
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.130.96 (0.009 с.) |

 (1.69)
(1.69) – ускорение движения ракеты в момент времени t,
– ускорение движения ракеты в момент времени t, за время Т.
за время Т.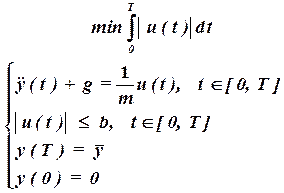 (1.70)
(1.70) эквивалентно системе уравнений:
эквивалентно системе уравнений: (1.71)
(1.71)
 .
.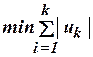
 . (1.72)
. (1.72)
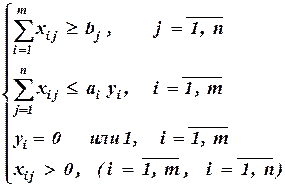 (1.73)
(1.73) ). Каждой трубе соответствует одно ограничение, которое означает, что для получения к ней доступа необходимо приподнять, по крайней мере, одну из плит.
). Каждой трубе соответствует одно ограничение, которое означает, что для получения к ней доступа необходимо приподнять, по крайней мере, одну из плит.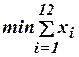
 . (1.74)
. (1.74) 1
1



