Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципы системного анализа.Содержание книги Поиск на нашем сайте
Принципы системного анализа. Системный анализ и исследование операций
Дисциплина, именуемая «системный анализ», родилась в силу необходимости вести исследования междисциплинарного характера. Поэтому в соответствии с [12] можно принять за основу следующее определение: Системный анализ представляет собой научное направление, связанное с исследованием слабоструктурированных сложных проблем междисциплинарного характера. Он включает в себя и создание сложных технических систем, проектирование больших технологических, энергетических, гидротехнических, информационных комплексов, анализ экономических и экологических ситуаций, и многие другие направления инженерной, научной и хозяйственной деятельности. Решение этих задач требует объединения усилий специалистов разных научных профилей, унификации и согласования информации, получаемой в результате исследований конкретного характера. Системный анализ является необходимой методической базой для проведения системных исследований. Предметом системных исследований могут быть различного рода объекты, процессы, явления, а также связанные с ними проблемы. В рамках системных исследований решаются два основных класса задач: Задачи анализа объекта исследования. Задачи синтеза наилучшего в определенном смысле варианта решения проблемы.
Системный анализ как научное направление базируется на четырех основополагающих принципах: системности, иерархичности, интегральности и формализма [13, 23].
Принцип системности требует всестороннего, многоаспектного, целостного, целеориентированного подхода к исследуемому предмету, исходя из возможного набора сфер его существенного проявления и назначения.
Принцип иерархичности требует многоуровневого рассмотрения предмета исследований.
Принцип интегральности требует выявления, в первую очередь, общих свойств предмета исследований, дающих о нем целостное представление. Этот принцип базируется на фундаментальном свойстве систем, которое может быть сформулировано следующим образом:
Свойства системы не есть простая сумма свойств, составляющих ее частей.
В силу этого нельзя получить адекватного представления о системе, изучая по отдельности ее компоненты.
Принцип формализма требует построения формальных моделей исследуемого объекта, Результатом системных исследований является, как правило, выбор вполне определенной альтернативы (решения). Таким образом, системный анализ – это дисциплина, занимающаяся проблемами принятия решений в условиях, когда выбор альтернативы требует анализа сложной информации различной физической природы. Поэтому истоки системного анализа, его методических концепций лежат в тех дисциплинах, которые занимаются проблемами принятия решений. Одной из основных дисциплин такого рода является исследование операций. Термин "операция" достаточно общий, он означает любое целенаправленное действие. Исследование операций нельзя считать дисциплиной чисто математической, хотя она широко использует математические методы и породила целый ряд направлений прикладной математики. Главным же содержанием дисциплины являются сложные проблемы принятия решений, при изучении которых неформальные методы, представления здравого смысла и способы описания – математическая формализация, – играют не меньшую роль, чем формальный математический аппарат.
Принципы принятия решений Неопределённость целей. Выделение главного критерия
Предположим, что введена некоторая система показателей
Среди показателей
при ограничениях (1.2), где Такая схема редукции многокритериальной задачи к однокритериальной является, вероятно, самой простой и наиболее употребительной в практике. При этом следует заметить следующее [32]:
1. Переход от исходной задачи (1.1) к задаче (1.3) не есть переход от одной эквивалентной задачи к другой. 2. Не всегда ясен алгоритм определения границ
3. Возможно наличие нескольких «главных» критериев, находящихся в противоречии друг с другом. Метод максиминной свёртки Задаётся некоторая система нормативов:
В таких случаях интегральный критерий удобно представить в виде:
и искать вектор х *, который обеспечивает максимальное значение F(x). Если значения
Компромиссы Парето
Все рассмотренные выше способы разрешения многокритериальной проблемы выбора были основаны на различных операциях свёртывания скалярных критериев к интегральным. К решению многокритериальных задач можно подойти с других позиций – попытаться сократить множество исходных вариантов, т. е. исключить из неформального анализа те варианты решений, которые заведомо плохи. Один из подобных путей был предложен итальянским экономистом Парето в 1904 г. Для раскрытия содержания этого подхода воспользуемся теоретико-множественной интерпретацией, для чего введём следующие операции и понятия [33].
Содержательный смысл этого определения состоит в том, что задание подмножества R на множестве W x W определяет, какие пары находятся в отношении R. Это подчёркивается следующим соглашением об обозначениях: если пара
Множество W называется областью задания отношения и в тех случаях, где существенна область задания отношения, используется пара обозначений Пример 1.1
Пусть W 1 – множество студентов группы, W 2 – множество студентов факультета, W 3 – множество студентов всего института. Естественно определяются три разных отношения: Способы задания отношений
Существуют три основных способа задания отношений: · матрицей, · графом, · сечениями.
Матричный способ. Общее правило задания матрицы отношения формулируется так:
где
Задание графом Элементы конечного множества W – вершины графа. От элемента Задание сечениями. Этот способ менее распространён, чем предыдущие, однако он пригоден и для задания отношений на бесконечных множествах.
Таким образом, множество Множество
На рис 1.1 изображены верхнее и нижнее сечения отношения Р в точке
Из определения множества следует, что Пример 1.2 Пусть
Множества  и и  изображены на рис. 1.2. изображены на рис. 1.2.
Легко видеть, что
Таким образом, множество Парето Переходя к многокритериальному пространству где хТ = [ х1, х2,..., х j,.,. хn ], отношение Парето в соответствии с определением 4 представляет собой следующее отношение доминирования:
Множество, включающее в себя все эффективные элементы х множества Отображение множества Заметим, что принцип Парето не выделяет единственного решения, он только сужает множество альтернатив, окончательный выбор остаётся за ЛПР на основе дополнительной информации о его предпочтениях. Метод парного сравнения
Данный метод заключается в установлении предпочтений при сравнении двух критериев. Матрица предпочтений А составляется следующим образом:
Таким образом, значение «1» при сравнении двух критериев выставляется лишь в том случае, если i - й критерий более предпочтителен, чем j - й или эквивалентен ему. Результаты обработки ряда (1.17) по методу парных сравнений представлены матрицей А (табл.1.3).
Таблица 1.3
А. Ранжирование
Ранжирование
Для построения средней оценки вводится в соответствии с [33] понятие расстояния между ранжировками
При наличии m ранжировок Медиана Кемени
где m – число экспертов,
Наряду с принципом Кемени, для выбора результирующего ранжирования часто используется принцип большинства. Он состоит в следующем: на первое место в результирующую ранжировку попадает критерий, который большинство экспертов поставили на первое место, на второе – критерий, который поставили на второе и т. д. Однако, как показано в [33], данный принцип в отличие от принципа Кемени не всегда приводит к выбору наилучшего решения. Примеры построения операционных моделей Пример 1.8. Линейные модели Транспортная задача Предположим, что однородный продукт должен быть перевезен из т пунктов производства в п пунктов потребления, причем из каждого пункта производства вывозится установленное количество и в каждый пункт потребления ввозится также установленное количество продукта, так что общие спрос и предложение равны. Пусть из i -го пункта производства (i =1, 2,..., m) вывозится ai продукта, а в j -й пункт потребления должно быть ввезено bj продукта, причем величины эти известны. Тогда:
где Пусть xi j – неизвестное количество продукта, которое должно быть перевезено из i -го пункта производства в j -й пункт потребления. Тогда:
где Пусть стоимость перевозки из i -го пункта производства в j -й пункт потребления равна
Задача поставщика
Владелец кафе знает, что в связи с наступлением праздников в течение одной следующей недели ему в j -й день (
На стирку обычно требуется три дня, т.е. грязная салфетка отправленная в стирку в j -й день, вернется из стирки и может быть использована в (j+3) -ийдень. Однако в прачечной существует ускоренное обслуживание по повышенному тарифу, при котором салфетки возвращаются из стирки через два дня. Не имея на руках или в прачечной готовых к употреблению салфеток, владелец будет вынужден покупать салфетки по 25 рублей за штуку. Стоимость стирки – 10 и 15 рублей соответственно при обычном обслуживании и при ускоренном обслуживании. Как должен вести дело владелец кафе, чтобы удовлетворить потребность кафе в салфетках и минимизировать издержки за неделю? Построим математическую модель. Пусть x i, ( Так как необходимо минимизировать общую сумму, требуемую для поддержания количества салфеток на должном уровне, не следует покупать салфеток больше, чем требуется в данный день, или отправлять салфетку в прачечную, если она не будет использована в дальнейшем.
В первый день, т.е. в понедельник, необходимо купить такое количество салфеток, какое требуется, т.е. x 1 = 5. В этот день можно выбирать: послать ли все или некоторые из пяти грязных салфеток в быструю, медленную прачечную или оставить их в ящике для грязных салфеток. То, что происходит с этими пятью салфетками можно представить уравнением:
y1 + z1 + u1 = 5. (1.54)
Общая стоимость всех операций первого дня:
25x1 +15y1 + 10z1 (1.55)
Выпишем остальные ограничения данной модели, помня о том, что в нашей системе выстиранные салфетки возвращаются через 2 или 3 дня в зависимости от того, какой прачечной мы воспользовались.
Во вторник необходимо купить некоторое количество салфеток, а именно x2 = 6. После того, как их используют, мы поступим с ними и u1 грязными салфетками согласно уравнению: y2 + z2 + u2 = 6 + u1. (1.56)
Оно выражает тот факт, что у нас скопилось u1 грязных салфеток, оставшихся с понедельника и еще 6, оставшихся со вторника. Можно их отправить в стирку (y2 + z2), либо оставить в ящике с грязными салфет-ками (u2). Стоимость всех операций во вторник:
25x2 + 15y2 + 10z2. (1.57)
В среду нам потребуется 7салфеток. Это первый день, когда выстиранные салфетки из быстрой стирки можно употребить в дело. Поэтому нужные 7 салфеток можно получить, купив их или взяв их из того количества салфеток, которые были сданы в стирку в понедельник. Имеем:
x3 + y1 = 7. (1.58) Так же, как и ранее y3 + z3 + u3 = 7 + u2, (1.59)
а стоимость операции в среду равна:
25x3 + 15y3 + 10 z 3. (1.60)
Необходимые в четверг 8 салфеток могут быть либо новыми, либо выбранными из числа тех, которые мы посылали в быструю прачечную во вторник или в медленную прачечную в понедельник. Это можно записать как: x4 + y2 + z1 = 8 (1.61) y4 + z 4 + u4 = 8 + u3, (1.62)
а стоимость операций в четверг составит:
25x4 + 15y4 + 10z4.
Предположим, что нас интересует только одна неделя и, следовательно, мы не будем отдавать салфетки в стирку, если они не вернутся назад к воскресенью. Для пятницы имеем: x5 + y3 + z2 = 7. (1.63) y5 + u5 = 7 + u4 (1.64) а стоимость равна: 25x5 + 15y5. (1.65) Для субботы: x6 + y4 + z3 = 9 (1.66)
u6 = 9 + u5, а стоимость равна 25 x6 .
Для воскресенья имеем: x7 + y5 + z4 = 10 (1.67) u7 = 10 + u6, а стоимость равна 25 x7.
Объединяя полученные выше уравнения, получаем математическую модель операции:
при условиях:
Пример 1.9. Нелинейные модели Пример 1.10. Целочисленные модели Задача о размещении Рассмотрим какую-нибудь отрасль промышленности, выпускающую товары широкого потребления, которые прямо с заводов отправляются в торговые предприятия. Требуется ответить на вопрос, где разместить каждое из промышленных предприятий и каковы должны быть их производственные мощности. При этом известно местонахождение каждой торговой точки, занимающейся розничной продажей товаров данной отрасли промышленности и известны потребности каждой из этих точек. Пусть b1,b2,..., bn, – объемы продукции, необходимые для покрытия потребностей «п» имеющихся торговых точек, a1,a2,..., am – производственные мощности «т» заводов, о размещении которых идет речь. Допустим, что известна стоимость каждого из заводов: стоимость строительства i - го завода обозначим через fi. Расходы на доставку единицы продукции от i -го завода до j -ой торговой точки равны ci j. Предположим, что i -м заводом j - й торговой точке поставляется xi j единиц продукции. Введем переменную yi, такую, что
yi = 1, если i - й завод решено построить; yi = 0, если i - й завод решено не строить. Задача заключается в том, чтобы минимизировать сумму расходов на строительство заводов и доставку товара торговым точкам при полном удовлетворении спроса потребителей.
Математическая модель задачи выглядит следующим образом:
при условиях: Если было бы заранее известно, какие заводы и где решено построить, все свелось бы к решению обычной транспортной задачи (пример 1.8). Задача о водопроводчике
Водопроводчик получил наряд на установку вентилей на нескольких трубах, проложенных под землей, покрытой тяжелыми квадратными плитами (рис. 1.3). Он может установить механизмы перекрытия в любом месте трубы, но, разумеется, лишь по одному шлюзовому затвору на каждой трубе. Для минимизации трудозатрат водопроводчику надо определить минимальное число плит, которые требуется приподнять, чтобы установить по одному затвору на каждой трубе. Пронумеруем плиты от 1 до 12. Пусть x i = 0, если выбранное решение состоит в том, чтобы не приподнимать i - ю плиту, x i = 1, если принимается решение приподнять i - ю плиту (
Математическая модель задачи выглядит следующим образом:
при условиях:
Эта задача попадает в класс так называемых задач о «покрытии множества», для которого характерны разнообразные практические приложения.
Рис 1.3
Пример 1.11. Стохастические модели
Задачи
1. Диспетчерская служба имеет следующие минимальные потребности в количестве диспетчеров в различное время суток (табл. 1.6):
Таблица 1.6
При этом нужно иметь в виду, что период 1 следует сразу же за периодом 6. Каждый диспетчер ежедневно приступает к работе в начале определенного периода и работает восемь часов без перерыва. Требуется составить расписание на каждые сутки таким образом, чтобы обойтись минимальным числом диспетчеров, не нарушая, при этом, сформулированных выше требований.
2. В обработку поступили две партии досок для изготовления комплектов из трех деталей, причем первая партия содержит 50 досок длиной по 6,5 м, вторая содержит 200 досок длиной 4 м. Каждый комплект состоит из двух деталей по 2 м каждая и одной детали по 1,25 м. Как распилить доски, чтобы получить наибольшее число комплектов?
3. На заводе предстоит решить, какое количество х1 чистой стали и какое количество х2 металлолома следует использовать для приготовления (из соответствующего сплава) литья для одного из своих заказчиков. Пусть производственные затраты на 1 т стали составляют 3 усл. ед., а затраты на 1 т металлолома 5 усл. ед. (последняя цифра больше предыдущей, т.к. использование металлолома связано с его предварительной очисткой). Заказ предусматривает поставку не менее 5 т литья. Предположим, что предназначенные для литья запасы чистой стали составляют 4 т, а металлолома – 6 т. Отношение веса металлолома к весу чистой стали в сплаве не должно превышать 7/8. Производственно-технологические условия таковы, что на процессы плавки и литья может быть отведено не более 18 час., при этом на 1 т стали затрачивается от 2,5 до 3 час., а на 1т металлолома от 1,5 до 2 час. Цель завода – выполнить заказ с минимальными производственными затратами. 4. Предприятие выпускает радиоприемники трех различных моделей: модель А, модель В и модель С. Каждое изделие указанных моделей приносит доход в размере 8, 15, 25 единиц стоимости соответственно. Необходимо, чтобы фирма выпускала не менее 100 приемников модели А, 150 приемников модели В и 75 приемников модели С. Каждая модель характеризуется определенным временем, необходимым для изготовления соответствующих деталей, сборки изделия и его упаковки. Так, в частности, в расчете на 10 приемников модели А требуется 3 ч. для изготовления соответствующих деталей, 4 ч. на сборку и 1 ч. на упаковку. Соответствующие показатели на 10 приемников модели В равняются 3; 5, 5 и 1,5 ч., а на 10 приемников модели С – 5, 8 и 3. В течение ближайшей недели фирма может израсходовать на производство – 150 ч., на сборку – 200 ч. и на упаковку – 60 ч. Составить производственный план. 5. На предприятии требуется произвести раскрой рулона материала шириной 60 см. Мастер сообщил следующие данные о заказах текущей недели:
Предполагается, что количество рулонов с шириной 60 см достаточно для того, чтобы удовлетворить все недельные заказы. Найти план раскроя, минимизирующий общие суммарные потери.
6. В небольшом населенном пункте А имеется школа, которую посещает некоторое число учеников, при этом место жительства 72 учеников находится вне населенного пункта, что приводит к необходимости организовать их доставку к школе на автобусах. Имеются две основные автобусные остановки В, С (В находится между А и С). Число учеников, нуждающихся в доставке к школе на автобусе равняется 42 на остановке С, 6 – между С и В, 20 на остановке В и 4 – между В и А (рис.1.4).
Рис. 1.4
Транспортное агентство, обслуживающее пункт А, располагает двумя типами автобусов: автобусы на 35 и 50 мест. Транспортным агентством установлены следующие цены проездных билетов для каждого из отрезков пути в зависимости от типа автобуса:
Необходимо определить, какого типа автобусы следует использовать на каждом участке пути так, чтобы суммарные издержки школьников были минимальными.
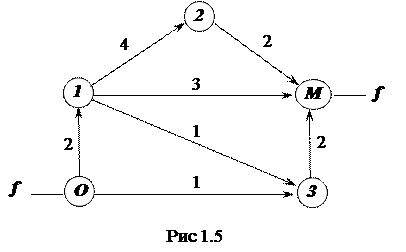
7. Определить максимальный поток f из пункта О в пункт М при ограниченной пропускной способности путей. Граф путей представлен на рис 1.5.
Числа над дугами графа определяют верхнюю границу потока на соответствующих путях.
8. Информация о проекте задана перечнем работ, их продолжительностью и последовательностью выполнения (табл. 1.7):
Таблица 1.7
В i - ю работу можно вложить средства, где xi £ ci, при этом время выполнения работы уменьшится до t i(1 - bi xi).
Пусть: b1 = 0.2, c1 = 2, b4 = 0.3, c4 = 2, b8 = 0.1, c8 = 5. Определить размер вложенных средств x1 , x4 , x8 в 1-ю, 4-ю, 8-ю работы так, чтобы время завершения всего комплекса работ не превышало 40 месяцев. Сформулировать общую задачу минимизации суммы вложений, необходимых для того, чтобы обеспечить завершение всего комплекса работ к заданному моменту в
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.017 с.) |


 позволяющего получить конструктивные результаты и сделать необходимые позитивные выводы. Однако этот принцип не исключает возможности использования неформальных методов и процедур.
позволяющего получить конструктивные результаты и сделать необходимые позитивные выводы. Однако этот принцип не исключает возможности использования неформальных методов и процедур. относительно которых
относительно которых  должен удовлетворять ограничениям:
должен удовлетворять ограничениям: (1.2)
(1.2) Тогда переходим к однокритериальной задаче:
Тогда переходим к однокритериальной задаче: (1.3)
(1.3)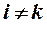 .
.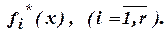
 . Это значит, что параметры будущего проекта должны быть таковы, чтобы максимизировать функции
. Это значит, что параметры будущего проекта должны быть таковы, чтобы максимизировать функции 
 (1.10)
(1.10) жестко не заданы, то они могут быть определены в результате экспертного опроса.
жестко не заданы, то они могут быть определены в результате экспертного опроса. .
.
 входит в R, т. е.
входит в R, т. е.  , то пишут x R y, что читается: “ x находится в отношении R с y ”.
, то пишут x R y, что читается: “ x находится в отношении R с y ”. .
. ,
,  ,
,  , где
, где 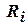 – множество таких пар
– множество таких пар  ,
,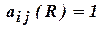 , если выполнено
, если выполнено  ,
, , если не выполнено
, если не выполнено  к элементу
к элементу  проводится дуга тогда и только тогда, когда выполнено
проводится дуга тогда и только тогда, когда выполнено  ) превращается в петлю при вершине
) превращается в петлю при вершине  ).
). таких, что
таких, что  ;
;
 . (1.11)
Аналогично определяется нижнее сечение:
. (1.11)
Аналогично определяется нижнее сечение:
 . (1.12)
. (1.12)
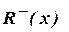 – это множество всех элементов
– это множество всех элементов  находится в отношении
находится в отношении  .
. – это множество всех элементов
– это множество всех элементов  с фиксированным элементом
с фиксированным элементом  называется дополнением отношения
называется дополнением отношения  \
\ 

 (1.13)
где множество
(1.13)
где множество  – n -мерное пространство
– n -мерное пространство  .
.


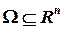 называется множество:
называется множество:
 . (1.14)
. (1.14)
 содержит те и только те элементы х* для которых
содержит те и только те элементы х* для которых  .
. ;
;

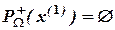 ,
,  ,
, ,
, ,
, ,
,  .
. и
и  .
. , где
, где  и множеству решений х Î Х,
и множеству решений х Î Х,


 Определение 6
Определение 6
 не существует более предпочтительной по Парето точки, т.е. такой точки х, что
не существует более предпочтительной по Парето точки, т.е. такой точки х, что  , тогда
, тогда  называется
эффективным или Парето-оптимальным решением многокритериальной задачи:
называется
эффективным или Парето-оптимальным решением многокритериальной задачи:
 .
.
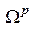 , называется множеством Парето и обозначается
, называется множеством Парето и обозначается  .
. и называется множеством эффективных оценок. Смысл введённого понятия состоит в том, что оптимальный исход следует искать среди элементов множества недоминируемых элементов
и называется множеством эффективных оценок. Смысл введённого понятия состоит в том, что оптимальный исход следует искать среди элементов множества недоминируемых элементов  , оказывающаяся более предпочтительной с учётом всех частных целевых функций
, оказывающаяся более предпочтительной с учётом всех частных целевых функций 
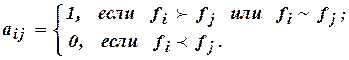
 проведёнными k –ым и l –ым экспертами:
проведёнными k –ым и l –ым экспертами: . (1.21)
. (1.21)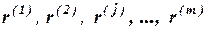 , проведённых m экспертами, результирующей считается та сумма расстояний от которой до исходных есть величина наименьшая из всех возможных. Такая ранжировка называется медианой Кемени.
, проведённых m экспертами, результирующей считается та сумма расстояний от которой до исходных есть величина наименьшая из всех возможных. Такая ранжировка называется медианой Кемени. находится из задачи минимизации по всем возможным ранжировкам из множества R (таких ранжировок r!) суммы расстояний от r до
находится из задачи минимизации по всем возможным ранжировкам из множества R (таких ранжировок r!) суммы расстояний от r до  , т.е. определяется формулой:
, т.е. определяется формулой: , (1.22)
, (1.22)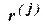 – ранжировка на множестве критериев, проведённая j -м экспертом.
– ранжировка на множестве критериев, проведённая j -м экспертом. , (1.50)
, (1.50) для всех i ¹ j.
для всех i ¹ j. (1.51)
(1.51) , (1.52)
, (1.52) ³ 0 для всех i и j.
³ 0 для всех i и j. . Эти величины также заданы. Задача состоит в том, чтобы найти
. Эти величины также заданы. Задача состоит в том, чтобы найти  . (1.53)
. (1.53) ) потребуется rj чистых салфеток:
) потребуется rj чистых салфеток: ) количество новых салфеток, купленных в соответствующий день недели, Аналогично, пусть y i, z i, (
) количество новых салфеток, купленных в соответствующий день недели, Аналогично, пусть y i, z i, (



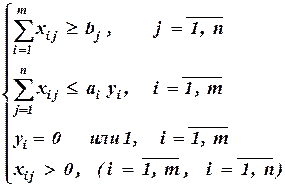 (1.73)
(1.73) ). Каждой трубе соответствует одно ограничение, которое означает, что для получения к ней доступа необходимо приподнять, по крайней мере, одну из плит.
). Каждой трубе соответствует одно ограничение, которое означает, что для получения к ней доступа необходимо приподнять, по крайней мере, одну из плит.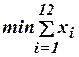
 . (1.74)
. (1.74) 1
1

 А (4) В (20) (6) С (42)
А (4) В (20) (6) С (42)