В чем суть теории нормализации реляционной модели данных.

В чем суть теории нормализации реляционной модели данных.

Теория нормализации схем отношений реляционной модели
данных – это теория, устанавливающая:

· каким образом исходная схема отношений может быть
преобразована в другую результирующую схему, которая

· эквивалентна в некотором смысле исходной и

· в каком-то смысле лучше ее.

Таким образом эта теория должна ответить на следующие вопросы:

· какие существуют критерии эквивалентности схем
отношений;

· какие существуют критерии оценки качества схем
отношений;

какие существуют механизмы эквивалентных преобразо-
ваний схем отношений, дающие более качественные схемы

 

Почему схемы реляционных баз данных могут быть плохими. Примеры

· Установлен предел в 9 покупок, а что если их больше?

· Если покупок меньше 9, то следует устанавливать значения NULL
для остальных покупок! Что делать если необходимо удалить
покупку в середине списка?

· Как поступать в том случае, когда следует упорядочивать
покупки одного покупателя.

· Как должно выглядеть условие поиска покупателей, купивших
товар с номером 2?:
(НТ1 = 2) OR (НТ2 = 2) OR (НТ3 = 2)... OR (НТ9 = 2)

 

· Аномалии вставки. Нельзя вставить одни данные в связи с тем,
что не определены другие данные.

· Аномалии обновления. Может возникнуть потеря целостности.
в связи с избыточностью данных и их частичным обновлением.

· Аномалии удаления. При удалении одних данных можно
потерять другие данные.

Причина! Такая ситуация возможна, когда в одном отношении хранится информация о нескольких сущностях

 

Сложные домены и первая нормальная форма. Примеры

Нормализация – это пошаговый обратимый процесс эквивалентного преобразования одной схемы отношений в другую, которая обладает улучшенными характеристиками по сравнению с предыдущей. Каждый из таких этапов преобразования называется нормальной формой.

Виды нежелательных свойств отношений и нормальные формы,
которые их устраняют:

 

· Составные (неатомарные) данные - 1NF

· Неполная (частичная) функциональная зависимость - 2NF

· Транзитивная функциональная зависимость - 3NF

· Многозначная зависимость - 4NF

Зависимость по соединению

 

Отношение находится в первой нормальной форме (1NF), если все его атрибуты построены на атомарных (простых) доменах, и, следовательно, значения в ячейках таблицы являются простыми.

Отношение называется нормализованным, если оно находится в 1NF

 

4) Функциональная зависимость. Основные определения. Примеры

Пусть задано отношение R, которое содержит наборы атрибутов A и B. В отношении R B функционально зависит от A и А функционально определяет В, тогда и только тогда, когда каждое значение проекции R[А] в любой момент времени связано точно с одним значением проекции R[В]. Эта ФЗ обозначается следующим образом: R.А ® R.В. (или.А ® В). Набор атрибутов А называют детерминантом для набора атрибутов В.

Формальное определение функциональной зависимости (FD):

 

 

Наличие функциональной зависимости является свойством схемы, а не того или иного экземпляра отношения, и отражает семантику моделируемой предметной области.

 

Ключи отношения с точки зрения функциональной зависимости. Примеры

Набор К атрибутов отношения R называется суперключом отношения R, если все атрибуты R функционально зависит от К.

 

Набор К атрибутов отношения R называется возможным ключом отношения R, если верно, что:

o все атрибуты отношения R функционально зависит от К;

o ни один атрибут из набора К не может быть удален без нарушения свойства (а).

 

Формальное определение возможного ключа. Пусть М – полный набор атрибутов отношения R Подмножество атрибутов К отношения R является возможным ключом, если

· "А Í М R.K ® R.A

· "К' Ì K $B Í M R.K' ® R.B

Утверждение: Любое отношение имеет возможный ключ.

 

 

Свойства функциональных зависимостей. Примеры.

 

Свойства
1),2),3)составляют систему аксиом Армстронга

 

 

1) Транзитивность: если A ® B и B ® C, то A ® C.
2) Проективность: если B Í A, то A ® B
3) Аддитивность (объединение): если A® B и A® C, то A® (B,C)
4)Рефлексивность: A ® A.
5)Псевдотранзитивность: если А® В и (В,С)® D, то (A,C)®D
6) Продолжение: если А ® В, то (А, С) ® В для любого атрибута С.
7) Пополнение: если А ® В, то (А, С) ® (В, С) для любого атрибута С.
8) Декомпозиция: если А ® В и С Í В, то А ® С

 

Логическое следование функциональных зависимостей. Примеры

Пусть в отношении R имеется множество функциональных зависимостей F и конкретная зависимость А ® С, которая не входит в F. Зависимость А ® С логически следует из зависимостей F, если она может быть выведена из F с помощью аксиом функциональных зависимостей. Также говорят, что зависимость
А ® С выводима из F.

 

Например, если в R(A, B, C) и множество F состоит из А ® В, то из нее логически следуют (выводимы) следующие зависимости:

 

(А, С) ® В - применяется свойство продолжения;

(А, С) ® (В, С) - применяется свойство пополнения.

 

Замыкание, полнота, эквивалентность и минимальное покрытие функциональных зависимостей. Примеры

Пусть в отношении R имеется множество FD F. Множество всех FD, являющихся следствием (выводимыми) из F, называется (логическим) замыканием F, которое обозначается через F⁺. Очевидно, что F Í F⁺ и F⁺ = F⁺⁺.

Множество FD F образует полное семейство зависимостей, если F = F⁺.

Множества FD F и G (логически) эквивалентны, если F⁺ = G⁺.

 

Пусть задано множество FD F. Говорят, что множество FD G образует базис зависимостей F или, то же самое, образует минимальное покрытие F, если G является таким минимальным подмножеством F, что G⁺ =F⁺.

 

Неполная (частичная) функциональная зависимость и вторая нормальная форма. Примеры

 

Пусть в отношении R имеются наборы атрибутов А и В. Зависимость R.A ® R.B называется полной если В не зависит функционально ни от какого поднабора С Ì А, не содержащего В.

· Атрибут К-ВО полно функционально зависит от (НТ, НП, ДАТА)

· Атрибуты ИМЯ и ГОРОД полно функционально зависят от НП

· Атрибуты ИМЯ и ГОРОД не полно функционально зависят от (НТ, НП, ДАТА

 

 

Пример приведения в 2NF

 

Пример приведения в 2NF – итоги

· Исходное отношение содержит информацию о двух
сущностях, результирующие – каждое по одной сущности.

· Результирующие отношения не содержат аномалий
вставки, удаления, замены.

· Исходное отношение можно восстановить из
результирующих с помощью операции естественного
соединения.

· При таком разбиении не теряются функциональные
зависимости (то есть зависимости исходного и
результирующих отношений эквивалентны)

 

Транзитивная зависимость и третья нормальная форма. Примеры.

 

В отношении R присутствует транзитивная зависимость, если в нем имеются такие наборы атрибутов А, В, С, С Ë В, В Ë А что:

4 А ® В, В ® С; при этом В ® А

1) Условие В ® А необходимо, чтобы исключить тривиальную транзитивную зависимость типа следующей:

2) Условия С Ë В, В Ë А необходимы, чтобы исключить следующие тривиальные транзитивные зависимости:

 

Пример приведения в 3NF

Пример приведения в 3NF – итоги

o Исходное отношение содержит информацию о двух
сущностях, результирующие – каждое по одной
сущности.

o Результирующие отношения не содержат аномалий
вставки, удаления, замены.

o Исходное отношение можно восстановить из
результирующих с помощью операции естественного
соединения.

o При таком разбиении не теряются функциональные
зависимости (то есть зависимости исходного и
результирующих отношений эквивалентны)

 

Усиленная третья нормальная форма и нормальная форма Бойса-Кодда. Примеры

 

3NF требует отсутствия транзитивной зависимости именно непервичных атрибутов, а не всех атрибутов отношения. Усиленная 3NF требует отсутствия транзитивной зависимости
для ВСЕХ атрибутов отношения.

 

Это отношение находится в 3NF, но содержит информацию о двух сущностях и поэтому обладает аномалиями

 

Отношение находится в усиленной третьей нормальной форме, если оно находится во второй нормальной форме и не содержит транзитивных зависимостей ВСЕХ атрибутов от возможных ключей

 

Приведение в S3NF

Аксиомы MVD

Пусть R состоит из атрибутов (или набора атрибутов) А, В, С.

MVD обладают следующими аксиомами:

1) Аксиома дополнения

Если А ®® В, то А ®® С

2) Аксиома пополнения

Если А ®® В и V Í W, то (А, W) ®® (В, V)

3) Аксиома транзитивности

Если А ®® В и В ®® С, то А ®® С – В

Существуют следующие две аксиомы, которые связывают многозначные и функциональные зависимости.

1) Аксиома репликации

Если А ® В, то А ®® В

2) Аксиома соединения

Если А ®® В и Z Í B, и для некоторого W, непересекающегося с B имеем W ® Z, то A ® Z

 

Дополнительные свойства MVD

1) Объединение

Если А ®® В и А ®® С, то А ®® (В, С)

2) Псевдотранзитивность

Если А ®® В и (W, В) ®® Z,

то (W, А) ®® Z – (W, В)

3) Смешанная псевдотранзитивность

Если А ®® В и (А,В) ®® С, то А ®® (С - В)

4) Пересечение и разность

Если А ®® В и А ®® С,
то А ®® В Ç С, А ®® В – С, А ®® С – В

Четвертая нормальная форма. Примеры.

Отношение R находится в четвертой нормальной форме (4NF), если из существования в нем нетривиальной MVD
X ®® Y (где Y Ë Х) следует, что Х является суперключом отношения R.

Утверждение. Пусть отношение R состоит из атрибутов (или множеств атрибутов) А, В, С. Зависимость А ®® В имеет место в R тогда и только тогда, когда R = R[A, B] * R[A, C].

Алгоритм приведения к 4NF. Пусть задано отношение R с
атрибутами А, В, С, и имеется многозначная зависимость
R.A ®® R.B Тогда отношение R декомпозируются на
следующие два отношения: R[A, B] и R[B, С].

 

Если результирующие отношения все еще не находятся в
4NF, то к ним опять применяется этот алгоритм.

Многозначная зависимость называется встроенной, если она отсутствует в самом отношении, но существует в его проекциях по некоторым атрибутам.

 

15) Зависимость по соединению и пятая нормальная форма.

Пусть R является отношением с атрибутами (множествами атрибутов) А1, А2, …, Аn. Отношение R обладает зависимостью по соединению (JD) относительно А1, А2, …, Аn, что обозначается как *(А1, А2,…, Аn), если отношение R равно естественному соединению его проекций на А1, А2, …, Аn, то есть:

R = p_A1(R)*p_A2(R)*... * p_An(R) Û R = R[A1] * R[A2]*…*R[An])

JD является тривиальной, если один из наборов атрибутов Ai совпадает со множеством всех атрибутов отношения R.

JD является следствием возможных ключей отношения R, если все Ai (1 £ i £ n) являются суперключами R.

 

Требования к методологии проектирования БД

• Требования к методологии проектирования БД:
• Она должна приводить к созданию приемлемой
  структуры БД

• в разумные сроки,

• при разумных затратах,

• удовлетворяющей требованиям заказчика.

• Она должна быть достаточно общей, гибкой,
  доступной

Этап системного анализа ПО

 

Целью этапа анализа является проведение глубокого и всестороннего анализа содержимого ПО и фиксация результатов анализа в виде естественного языка

Методы анализа ПО:

· проведение всевозможных бесед с пользователями;

· интервьюирование и протоколирование;

· анализ циркулирующих в организации документов и бланков;

· анализ потока документов (документооборот);

· анализ решаемых в организации задач и способов их решения;

· фиксация всевозможных правил, ограничений, законов, действующих в ПО.

Язык ER-моделирования. Сущности. Примеры

Язык ER-моделирования - это язык определения информационной модели ПО. Базируется на концепции, согласно которой информационная модель ПО может быть описана в терминах: сущность, атрибут, связь. Используется на этапе анализа и прежде всего – концептуального моделирования. Язык является существенно графическим.

Сущность -это реальный или воображаемый объект, информация о котором подлежит сбору или хранению.

Графически сущность представляется поименованным прямоугольником с закругленными углами

Имя сущности дается в единственном числе заглавными буквами.

Любой объект может быть представлен только одной сущностью. Значит сущности всегда являются взаимоисключающими.

Каждая сущность должна быть уникально идентифицируема.
Это означает, что должен существовать способ независимой идентификации каждого экземпляра сущности, позволяющий отличать его от всех других экземпляров данного типа сущности.

Язык ER-моделирования. Атрибуты. Примеры

Язык ER-моделирования - это язык определения информационной модели ПО. Базируется на концепции, согласно которой информационная модель ПО может быть описана в терминах: сущность, атрибут, связь. Используется на этапе анализа и прежде всего – концептуального моделирования. Язык является существенно графическим.

Атрибут - это любая деталь или аспект, способствующие качественному или количественному описанию сущности, ее идентификации, классификации или отражению ее состояния.

Приводить атрибуты ER-схеме не обязательно. Желательно приводить обязательные и идентифицирующие атрибуты. Можно приводить атрибуты с примером его значения.

Язык ER-моделирования. Связи. Примеры

Язык ER-моделирования - это язык определения информационной модели ПО. Базируется на концепции, согласно которой информационная модель ПО может быть описана в терминах: сущность, атрибут, связь. Используется на этапе анализа и прежде всего – концептуального моделирования. Язык является существенно графическим.

Связь -это некоторая представляющая интерес поименованная ассоциация двух сущностей.

Связь является бинарной в том смысле, что это всегда ассоциация в точности двух сущностей или сущности с самой собой. Каждая связь имеет два конца, для каждого из которых имеются свои: имя; степень/мощность (один/много); Факультативность (обязательная/факультативная).

Представление связей

Именование и чтение связей

При чтении связи со обязательной стороны ее имя необходимо предварить словами " во всех случаях " или " всегда ",для факультативной стороны используются слова
" в общем случае " или " иногда ". Степень много читается как " один или несколько ", а степень один - " один и только один ".

Любой БИЛЕТ всегда выписывается на одного и только одного ПАССАЖИРа. Любой ПАССАЖИР в общем случае имеет на свое имя один или
не сколько БИЛЕТов.

Язык ER-моделирования. Допустимые и недопустимые связи. Примеры.

Язык ER-моделирования - это язык определения информационной модели ПО. Базируется на концепции, согласно которой информационная модель ПО может быть описана в терминах: сущность, атрибут, связь. Используется на этапе анализа и прежде всего – концептуального моделирования. Язык является существенно графическим.

Связь -это некоторая представляющая интерес поименованная ассоциация двух сущностей.

Связь является бинарной в том смысле, что это всегда ассоциация в точности двух сущностей или сущности с самой собой. Каждая связь имеет два конца, для каждого из которых имеются свои: имя; степень/мощность (один/много); Факультативность (обязательная/факультативная).

Язык ER-моделирования. Подтипы и супертипы. Примеры.

Язык ER-моделирования - это язык определения информационной модели ПО. Базируется на концепции, согласно которой информационная модель ПО может быть описана в терминах: сущность, атрибут, связь. Используется на этапе анализа и прежде всего – концептуального моделирования. Язык является существенно графическим.

Подтип - это разновидность сущности. Подтип неявно наследует все атрибуты и связи супертипа. Подтипы могут обладать собственными атрибутами и/или связями и, в свою очередь, разделяться на подтипы более низких уровней. Супертип - это систематизация сущностей с общими подтипами. Одна и та же сущность может являться супертипом и, в то же
время, представлять собой подтип другой сущности. Подтипы сущности образовывают полную систему множеств.

Пример типа/супертипа

НЕРЕГУЛЯРНЫЙ ПОЛЕТ и РЕГУЛЯРНЫЙ РЕЙСОВЫЙ ПОЛЕТ имеют один и тот же атрибут – НОМЕР (наследуется из супертипа РЕЙСОВЫЙ ПОЛЕТ), но отличаются связями!

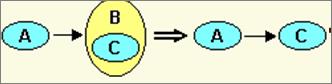
Сущность является простой, если она не является подтипом или сама не имеет подтипов.

Язык ER-моделирования. Разрешение связей многие-ко-многим. Примеры

Язык ER-моделирования - это язык определения информационной модели ПО. Базируется на концепции, согласно которой информационная модель ПО может быть описана в терминах: сущность, атрибут, связь. Используется на этапе анализа и прежде всего – концептуального моделирования. Язык является существенно графическим.

Взаимоисключающие связи

Две или более связей одной и той же сущности могут оказаться взаимоисключающими (либо-либо).

Этот факт представляется поперечной дугой, пересекающей окончания всех соответствующих связей, с небольшими точками или кружками в местах пересечения.

Создание пользователей

Любой пользователь для получения доступа к базе данных должен быть зарегистрирован в системе под определенным именем и определенным паролем.

Регистрация необходима для того, чтобы знать с кем имеет дело система в текущий момент работы.

Пользователь - это не только конкретное лицо, но и любой источник, который в состоянии обратиться к базе данных (программа, операционная система, Интернет-приложение и т.д.)

Создание ролей

Роль - это совокупность привилегий (прав) которые могут предоставляться группам пользователей или другим ролям.

Роли введены для того, чтобы можно было описывать ситуацию, когда группы пользователей имеют одинаковые функциональные обязанности, а значит они могут иметь одинаковые полномочия по работе с БД

Можно присвоить привилегии ролям, а затем «приписывать» пользователей к тем или иным ролям. Когда пользователь отнесен к роли, он получает привилегии этой роли

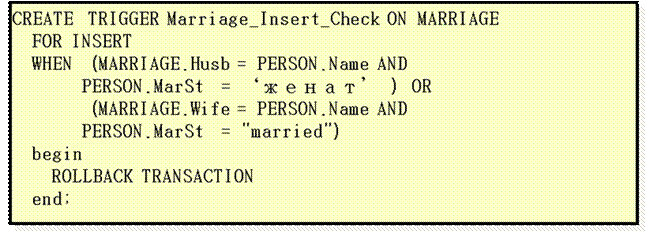
Пример операционно-ориентированного ограничения целостности

Пример: Вставка в базу данных информации о том, что х является
супругом y допустима только в том случае, если текущее
семейное положение x и y не есть женат/замужем

MARRIAGE(Husb, Wife), PERSON(Name, MarSt)

 

44) Целостность БД. Транзакции как механизм поддержания целостности

Тразакция – это последовательность предложений SQL, которые рассматриваются как единое целое.

Либо все предложения в транзакции выполняются успешно, либо ни одно из них не будет выполнено.

Это свойство поддерживается даже при выполнении транзакции произойдет программный или аппаратный сбой.

Транзакция преобразует базу данных из одного целостного состояния в другое, но в процессе выполнения транзакции целостность может нарушаться.

Транзакция гарантирует, что промежуточное противоречивое состояние базы данных будет невидимым для других пользователей.

Общая схема транзакции

 

 

 

В чем суть теории нормализации реляционной модели данных.

Теория нормализации схем отношений реляционной модели
данных – это теория, устанавливающая:

· каким образом исходная схема отношений может быть
преобразована в другую результирующую схему, которая

· эквивалентна в некотором смысле исходной и

· в каком-то смысле лучше ее.

Таким образом эта теория должна ответить на следующие вопросы:

· какие существуют критерии эквивалентности схем
отношений;

· какие существуют критерии оценки качества схем
отношений;

какие существуют механизмы эквивалентных преобразо-
ваний схем отношений, дающие более качественные схемы

 

Почему схемы реляционных баз данных могут быть плохими. Примеры

· Установлен предел в 9 покупок, а что если их больше?

· Если покупок меньше 9, то следует устанавливать значения NULL
для остальных покупок! Что делать если необходимо удалить
покупку в середине списка?

· Как поступать в том случае, когда следует упорядочивать
покупки одного покупателя.

· Как должно выглядеть условие поиска покупателей, купивших
товар с номером 2?:
(НТ1 = 2) OR (НТ2 = 2) OR (НТ3 = 2)... OR (НТ9 = 2)

 

· Аномалии вставки. Нельзя вставить одни данные в связи с тем,
что не определены другие данные.

· Аномалии обновления. Может возникнуть потеря целостности.
в связи с избыточностью данных и их частичным обновлением.

· Аномалии удаления. При удалении одних данных можно
потерять другие данные.

Причина! Такая ситуация возможна, когда в одном отношении хранится информация о нескольких сущностях

 

Сложные домены и первая нормальная форма. Примеры

Нормализация – это пошаговый обратимый процесс эквивалентного преобразования одной схемы отношений в другую, которая обладает улучшенными характеристиками по сравнению с предыдущей. Каждый из таких этапов преобразования называется нормальной формой.

Виды нежелательных свойств отношений и нормальные формы,
которые их устраняют:

 

· Составные (неатомарные) данные - 1NF

· Неполная (частичная) функциональная зависимость - 2NF

· Транзитивная функциональная зависимость - 3NF

· Многозначная зависимость - 4NF

Зависимость по соединению

 

Отношение находится в первой нормальной форме (1NF), если все его атрибуты построены на атомарных (простых) доменах, и, следовательно, значения в ячейках таблицы являются простыми.

Отношение называется нормализованным, если оно находится в 1NF

 

4) Функциональная зависимость. Основные определения. Примеры

Пусть задано отношение R, которое содержит наборы атрибутов A и B. В отношении R B функционально зависит от A и А функционально определяет В, тогда и только тогда, когда каждое значение проекции R[А] в любой момент времени связано точно с одним значением проекции R[В]. Эта ФЗ обозначается следующим образом: R.А ® R.В. (или.А ® В). Набор атрибутов А называют детерминантом для набора атрибутов В.

Формальное определение функциональной зависимости (FD):