Аномалии вставки, удаления, замены при наличии транзитивной зависимости

· Наличие в отношении транзитивной зависимости свидетельствует, что отношение содержит информацию о более, чем одной
сущности.

· Как следствие, такое отношение влечет аномалии вставки,
удаления, замены.

Третья нормальная форма (3NF)

Отношение находится в третьей нормальной форме, если оно находится во второй нормальной форме и не содержит транзитивных зависимостей непервичных атрибутов от возможных ключей.

Другими словами все непервичные атрибут должны функционально зависеть только от возможных ключей

Алгоритм приведения к 3NF. Пусть задано отношение R со множеством атрибутов M. Если в R имеется транзитивная функциональная зависимость R.A ® R.B и R.В ® R.С неключевого атрибута С от возможного ключа А, то отношение R разбивается на следующие два отношения: R[В, С] и R[M - С]. Если результирующие отношения все еще не находятся в третьей нормальной форме, то к ним опять применяется этот алгоритм.

Пример приведения в 3NF

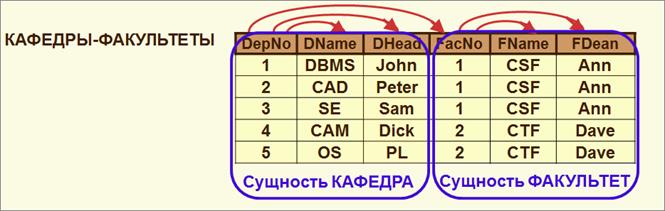
Пример приведения в 3NF – итоги

o Исходное отношение содержит информацию о двух
сущностях, результирующие – каждое по одной
сущности.

o Результирующие отношения не содержат аномалий
вставки, удаления, замены.

o Исходное отношение можно восстановить из
результирующих с помощью операции естественного
соединения.

o При таком разбиении не теряются функциональные
зависимости (то есть зависимости исходного и
результирующих отношений эквивалентны)

 

Усиленная третья нормальная форма и нормальная форма Бойса-Кодда. Примеры

 

3NF требует отсутствия транзитивной зависимости именно непервичных атрибутов, а не всех атрибутов отношения. Усиленная 3NF требует отсутствия транзитивной зависимости
для ВСЕХ атрибутов отношения.

 

Это отношение находится в 3NF, но содержит информацию о двух сущностях и поэтому обладает аномалиями

 

Отношение находится в усиленной третьей нормальной форме, если оно находится во второй нормальной форме и не содержит транзитивных зависимостей ВСЕХ атрибутов от возможных ключей

 

Приведение в S3NF

Алгоритм приведения к S3NF такой же, как в 3NF

 

 

Нормальная форма Бойса-Кодда (BCNF)

Отношение R находится в нормальной форме Бойса-Кодда, если любой детерминант является суперключом

Утверждение. Усиленная третья нормальная форма и нормальная форма Бойса-Кодда эквивалентны

 

12) Многозначная зависимость. Определение. Примеры.

Пусть задано отношение R с атрибутами (или наборами атрибутов) А, В, С. Говорят, что существует многозначная зависимость В от А (или А многозначно определяет В), и это обозначается как
А ®® В, если при заданных значениях атрибутов из А существует множество связанных значений атрибутов из В и это множество
В-значений не зависит от значений атрибутов из С.

Пример: В отношении УЧЕБА имеются следующие MVD:

Предмет ®® Преподаватель
Предмет ®® Учебник

Пусть задано отношение R(A,B). MVD А ®® Æ и А ®® В называются тривиальными так как они присутствуют во любых отношениях.

 

13) Свойства многозначных зависимостей. Примеры.

Аксиомы MVD

Пусть R состоит из атрибутов (или набора атрибутов) А, В, С.

MVD обладают следующими аксиомами:

1) Аксиома дополнения

Если А ®® В, то А ®® С

2) Аксиома пополнения

Если А ®® В и V Í W, то (А, W) ®® (В, V)

3) Аксиома транзитивности

Если А ®® В и В ®® С, то А ®® С – В

Существуют следующие две аксиомы, которые связывают многозначные и функциональные зависимости.

1) Аксиома репликации

Если А ® В, то А ®® В

2) Аксиома соединения

Если А ®® В и Z Í B, и для некоторого W, непересекающегося с B имеем W ® Z, то A ® Z

 

Дополнительные свойства MVD

1) Объединение

Если А ®® В и А ®® С, то А ®® (В, С)

2) Псевдотранзитивность

Если А ®® В и (W, В) ®® Z,

то (W, А) ®® Z – (W, В)

3) Смешанная псевдотранзитивность

Если А ®® В и (А,В) ®® С, то А ®® (С - В)

4) Пересечение и разность

Если А ®® В и А ®® С,
то А ®® В Ç С, А ®® В – С, А ®® С – В

Четвертая нормальная форма. Примеры.

Отношение R находится в четвертой нормальной форме (4NF), если из существования в нем нетривиальной MVD
X ®® Y (где Y Ë Х) следует, что Х является суперключом отношения R.

Утверждение. Пусть отношение R состоит из атрибутов (или множеств атрибутов) А, В, С. Зависимость А ®® В имеет место в R тогда и только тогда, когда R = R[A, B] * R[A, C].

Алгоритм приведения к 4NF. Пусть задано отношение R с
атрибутами А, В, С, и имеется многозначная зависимость
R.A ®® R.B Тогда отношение R декомпозируются на
следующие два отношения: R[A, B] и R[B, С].

 

Если результирующие отношения все еще не находятся в
4NF, то к ним опять применяется этот алгоритм.

Многозначная зависимость называется встроенной, если она отсутствует в самом отношении, но существует в его проекциях по некоторым атрибутам.

 

15) Зависимость по соединению и пятая нормальная форма.

Пусть R является отношением с атрибутами (множествами атрибутов) А1, А2, …, Аn. Отношение R обладает зависимостью по соединению (JD) относительно А1, А2, …, Аn, что обозначается как *(А1, А2,…, Аn), если отношение R равно естественному соединению его проекций на А1, А2, …, Аn, то есть:

R = p_A1(R)*p_A2(R)*... * p_An(R) Û R = R[A1] * R[A2]*…*R[An])

JD является тривиальной, если один из наборов атрибутов Ai совпадает со множеством всех атрибутов отношения R.

JD является следствием возможных ключей отношения R, если все Ai (1 £ i £ n) являются суперключами R.