
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конечность симплекс метода при решении канонической задачи линейного программированияСодержание книги
Поиск на нашем сайте
Решая каноническую задачу линейного программирования на минимум, мы выполняем ряд шагов. При этом на каждом шаге осуществляется либо переход от базиса исходного опорного решения к базису нового опорного решения, на котором значение целевой функции меньше, чем на исходном опорном решении, либо переход к очередному базису исходного опорного решения, если это опорное решения является вырожденным. Так как опорных решений у канонической задачи линейного программирования конечное число, то через конечное число шагов задача будет решена, т.е. либо будет найдено оптимальное решение, либо будет установлена неограниченность целевой функции на множестве допустимых решений этой задачи. Если задача имеет вырожденное опорное решение, то, переходя от одного его базиса к другому, можно вернуться к базису, который уже встречался ранее, и продолжать движение уже по пройденной последовательности базисов этого опорного решения. Такую ситуацию называют зацикливанием алгоритма симплекс метода. Чтобы избежать зацикливания, необходимо при переходе от одного базиса к другому ввести дополнительные условия. Рассмотрим симплекс таблицу, приведенную к базису В1,…,Bl,…,Bk,…,Br, опорного решения α.
Среди положительных одинаковых оценок симплекс таблице выбираем оценку Билет №25 Условия разрешимости канонической задачи линейного программирования на минимум Если каноническая задача линейного программирования н минимум имеет допустимое решение, а целевая функция на множестве допустимых решений ограничена снизу, то эта задача имеет оптимальное решение. Доказательство: в теореме о существовании опорного решения было доказано, что если каноническая задача линейного программирования имеет допустимое решение, то эта задача имеет и опорное решение. Принимаем это опорное решение за начальное опорное решение и решаем задачу симплекс методом. Так как целевая функция ограничена снизу на множестве допустимых решений, то через конечное число шагов симплекс метода будет найдено оптимальное решение данной задачи.
Билет №26
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.176 (0.007 с.) |


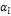



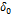
 } для всех a’is
} для всех a’is  0 выбираем наименьшее. Если указанное отношение не является единственным, то выбираем то, которое имеет наименьший номер i. применяя это правило на каждом шаге симплекс метода, будем получать базис системы условий задачи, который не встречался ранее. Поэтому через конечное число шагов задача будет решена.
0 выбираем наименьшее. Если указанное отношение не является единственным, то выбираем то, которое имеет наименьший номер i. применяя это правило на каждом шаге симплекс метода, будем получать базис системы условий задачи, который не встречался ранее. Поэтому через конечное число шагов задача будет решена.


