
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство системы линейных уравнений, содержащей тривиальное уравнение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Билет №1 Правило умножения матриц Пусть даны 2 матрицы A(m×n) и B(n×l), причем число столбцов матрицы A равно числу строк матрицы B. Тогда матрица C(m×l) с элементами
Билет №2 Свойство системы линейных уравнений, содержащей тривиальное уравнение. Тривиальное уравнение – уравнение, в котором коэффициенты при всех неизвестных и свободных членах равны нулю. Теорема: Система линейных уравнений, содержащая тривиальное уравнение, равносильна той же системе без тривиального уравнения. Доказательство: Рассмотрим СЛУ (1) и ту же СЛУ (2), но без тривиального уравнения.
(1) ……………………………………………………………… (2)
Пусть вектор Обратно, пусть вектор Таким образом, система линейных уравнений, содержащая тривиальное уравнение, равносильна этой же системе без тривиального уравнения.
Билет №3 Свойство свободных неизвестных в разрешенной СЛУ СЛУ называется разрешенной, если каждое уравнение системы содержит хотя бы одно разрешенное неизвестное. Теорема: Если в разрешенной СЛУ (4) придать свободным неизвестным Доказательство:
(4)
Подставим
(5)
Т. к. вектор Докажем единственность такого решения. Пусть вектор
(6)
Сопоставляя (5) и (6), видим, что Замечания: 1) Т. к. значения свободных неизвестных можно задать бесконечно большим числом способов, то система (4) является неопределенной. 2) Разрешенная СЛУ всегда совместна. При этом она определена, если m=n, т. е. число уравнений равно числу неизвестных, и не определена, если число уравнений меньше числа неизвестных, т. е. m<n
Билет №4 Решение системы однородных уравнений Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид: Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных. Доказательство: Допустим, система, ранг которой равен Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение. Доказательство: Если у системы уравнений Следствие 2: Однородная система Доказательство: Допустим, система
Билет №5 Примеры линейно зависимых и линейно независимых систем векторов 1) Система m -мерных векторов 2) Система m -мерных векторов Пример: Билет №6 Билет №7 Билет №8 Билет №9 Билет №10 Примеры задач линейного программирования: выпуск продукции, рацион, транспортная, портфель ценных бумаг.
Билет №11 Билет №12 Билет №13 Билет №14 Билет №15 Билет №16 Билет №17 Билет №18 Билет №19 Билет №20 Лемма о целевой функции Пусть δ₁,…,δј,…,δn оценки векторов условий задачи (1)-(3), приведенных к базису опорного решения α. Если вектор β=(l₁,…,lј,…,ln) является допустимым решением данной задачи, то f(β)=f(α)-∑ δј lј. Пусть векторы А₁, А₂, …, Аr являются базисом опорного решения α=(α₁,α₂,…,αr,0,0,…,0). Тогда симплекс таблица системы векторов условий задачи(1)-(3), приведенных к данному базису будет иметь вид:
Где по правилу построения строки (δ₁,…,δј,…,δn), оценки примут следующие значения: δ₁=δ₂=…=δr=0 и
Так как для базисных векторов А₁, А₂, …, Аr оценки равны нулю, то есть δ₁=δ₂=…=δr=0, то значение целевой функции на векторе β можно записать в виде: f(β)= γ₀+γ₁α₁+…+γr αr-δ r+₁ l r+₁- δ r+₂ l r+₂-…-δn ln=f(α)-∑ δј lј. Билет №21 Билет №22 Билет №23 Билет №24 Билет №25 Билет №26 Билет №27 Теорема (о методе искусственного базиса) Пусть вектор ß=(а1, а2,…, аn, an+1, an+2,…, an+m) является оптимальным решением искусственной задачи. Тогда: 1. если an+1=an+2=…=an+m=0,то вектор а=(а1, а2,…,an) является опорным решением исходной канонической задачи линейного программирования; 2. если среди чисел an+1, an+2,…, an+m, хотя бы одно отличается от нуля, т.е. найдётся an+1>0, i=1,2,…,m, то задача не имеет ни одного допустимого решения, т.е. система ограничений канонической задачи линейного программирования является несовместной. Доказательство. Докажем первое утверждение. По условию вектор ß =(а1, а2,…, аn, an+1, an+2,…, an+m) является оптимальным решением искусственной задачи. Тогда вектор ß является опорным решением этой задачи, а, следовательно, допустимым решением и, по определению, является решением системы линейных уравнений, т.е. выполняется соотношение: A1a1+A2a2+…+Anan+E1a n+1+E2an+2+…Eman+m=B, Так как an+1=an+2=…=an+m=0, то последнее равенство можно записать в виде A1a1+A2a2+…+Anan=B. Откуда по определению следует, что вектор а=(а1, а2,…,an) является допустимым решением исходной задачи. Так как вектор ß=(а1, а2,…, аn,0, 0,…, 0) является опорным решением искусственной задачи, то ненулевым координатам этого вектора соответствуют линейно независимые векторов условий этой задачи. Тогда некоторые из указанных линейно независимых векторов соответствуют ненулевым координатам вектора а=(а1, а2,…,an). Следовательно, вектор а является опорным решением исходной задачи. Второе утверждение теоремы будем доказывать от противного, предположив, что существует число аn+i >o, i=1,2,…,m, но при этом исходная задача имеет допустимое решение а=(k1,k2,…kn), которое удовлетворяет системе и kj≥, j=1,2,…,n. Тогда по определению допустимого решения выполняется соотношение: A1k1+A2k2+…+Ankn=B, которое можно переписать в виде A1k1+A2k2+…+Ankn+A n+10+An+20+…An+m0=B. Откуда следует, что вектор ß’=(k1, k2,…, kn,0, 0,…, 0) является допустимым решением искусственной задачи. Так как по условию вектор ß=(а1, а2,…, аn, an+1, an+2,…, an+m) является оптимальным решением искусственной задачи, то φ(а=(k1,k2,…kn),) ≤ φ(ß’), что равносильно неравенству: a n+1+an+2+…an+m≤0+0+…0. Однако, по предположению, существует a n+1>0, i=1,2,…,m, а следовательно, a n+1+an+2+…an+m>0. Получено противоречие. Таким образом, предположение о существовании допустимого решения исходной задачи является неверным. Следовательно, система ограничений исходной задачи является несовместной.
Билет №28 Доказательство. Значение целевой функции ЗЛП (1)-(4) на допустимом векторе а=(k1,…kn) с учетом доказанной леммы можно записать в виде f(a)=y1k1+…+yTkn+y0≤(∑i=1mai11j)k1+…+(∑mi=1ain1j)kn+y0=(a1111+…+am11m)k1+…+(a1n11+…+amn1m)kn+y0= (a11k1+…+a1nkn)11+…+(am1k1+…+am1kn)1m+y0=(∑j=1na1jkj)11+…+(∑j=1namjkj)1m+y0=b111+…+bm1m+y0≤φ(ß). Следовательно, f(a)≤φ(ß).
20. Если векторы а0 и ß0 являются допустимыми решениями взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно, и f(a0)=φ(ß0), то векторы а0 и ß0 – оптимальные решения этих задач соответственно. Доказательство. Для произвольного допустимого решения а задачи ЛП (1)-(4) по свойству 10 выполняется неравенство f(a)≤φ(ß0).так как по условию f(a0)= φ(ß0), то f(a)≤f(а0) и по определению вектор а0 является оптимальным решением ЗЛП (1)-(4). Оптимальность вектора ß0 доказывается аналогично.
30. Если целевая функция одной из взаимно двойственных задач ЛП неограниченна на множестве допустимых решений этой задачи, то другая взаимно двойственная задача ЛП не имеет ни одного допустимого решения, т.е. система условий этой задачи является несовместной. Доказательство. Доказательство проведем от противного. Пусть целевая функция - φ(ß) задачи ЛП (1’)-(4’) неограниченна снизу на множестве допустимых решений, а задача ЛП (1)-(4) имеет допустимое решение –а. тогда по свойству 10 для любого допустимого решения-ß задачи ЛП (1’)-(4’) должно выполняться неравенство f(a)≤φ(ß). Это неравенство противоречит неограниченности снизу целевой функции φ(ß) на множестве допустимых решений этой задачи. Следовательно, задача ЛП (1)-(4) не имеет ни одного допустимого решения, т.е. система условий этой задачи несовместна.
Билет №29 Теоремы двойственности Теорема 1. Если одна из взаимно двойственных задач ЛП имеет оптимальное решение, то и другая взаимно двойственная задача ЛП имеет оптимальное решение, при этом значения целевых функций на оптимальных решениях этих задач совпадают. Если же целевая функция одной из взаимно двойственных задач ЛП неограниченна на множестве допустимых решений, то вторая из взаимно двойственных задач ЛП не имеет ни одного допустимого решения, т.е., система условий второй задачи несовместна. Доказательство теоремы следует из сформулированных выше свойств. Теорема 2. Пусть векторы a0=(x10,…,xn0) и ß0=(y10,…,ym0) являются допустимыми решениями взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно. Для того, чтобы векторы a0 и ß0 были оптимальными решениями этих задач необходимо и достаточно выполнение следующих равенств: { xj0(∑mi=1aijyj0-yj)=0, j=1,2,…,n; {yi0(∑nj=1aijx0j-bi)=0, i=1,2,…,m. Доказательство. Необходимость. Пусть векторы a0 и ß0 оптимальные решения взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно. Тогда по свойству 20 выполняется равенство f(a0)=φ(ß0), которое можно записать в виде: y1x10+…+ynxn0+y0=b1y10+…+bmym0+y0. Это равенство с учётом соотношения (∑aijyi0)xj0≥yjxj0,j=1,2,…,n,равносильно неравенству: (∑ai1yi0)x10+…+(∑aiTyi0)xT0≥b1y10+…+bmym0 В то же время, из условий задач (1)-(4) и (1’)-(4’) следует, что каждое слагаемое в последнем неравенстве неположительное. Поэтому и все выражение в левой части этого неравенства должны быть не положительны. Следовательно в последнем отношении должно быть равенство, т.е. (∑a1jxj0-b1)y10+…+(∑amjxj0-bm)ym0=0. Однако сумма положительных слагаемых может равняться нулю только тогда, когда каждое слагаемое равно нулю. Таким образом, необходимость для выполнения второго соотношения в утверждении теоремы доказана. Необходимость для выполнения первого соотношения в утверждении теоремы доказывается аналогично. Достаточность. Пусть выполняются равенства: { xj0(∑mi=1aijyj0-yj)=0, j=1,2,…,n; {yi0(∑nj=1aijx0j-bi)=0, i=1,2,…,m. Тогда f(a0)=y1x10+…+ynxn0+y0=xj0(∑aijyi0)+…+xj0(∑aijyi0)+y0=(a11y10+…+am1ym0)x10+…+(a1ny10+…+amnym0)xn0+y0= =b1y10+…+bmym0+y0=φ(ß0)
Т.е. f(a0)= φ(ß0). Откуда с учётом свойства 20 следует, что векторы a0 и ß0 оптимальные решения взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно.
Билет №30 Билет №31 Билет №1 Правило умножения матриц Пусть даны 2 матрицы A(m×n) и B(n×l), причем число столбцов матрицы A равно числу строк матрицы B. Тогда матрица C(m×l) с элементами
Билет №2 Свойство системы линейных уравнений, содержащей тривиальное уравнение. Тривиальное уравнение – уравнение, в котором коэффициенты при всех неизвестных и свободных членах равны нулю. Теорема: Система линейных уравнений, содержащая тривиальное уравнение, равносильна той же системе без тривиального уравнения. Доказательство: Рассмотрим СЛУ (1) и ту же СЛУ (2), но без тривиального уравнения.
(1) ……………………………………………………………… (2)
Пусть вектор Обратно, пусть вектор Таким образом, система линейных уравнений, содержащая тривиальное уравнение, равносильна этой же системе без тривиального уравнения.
Билет №3
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1037; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.008 с.) |

 ,
,  (т.е. i-тая строка матрицы A, умноженная скалярно на j-й столбец матрицы B, дает cij-й элемент матрицы C, стоящий в i-й строке и j-м столбце).
(т.е. i-тая строка матрицы A, умноженная скалярно на j-й столбец матрицы B, дает cij-й элемент матрицы C, стоящий в i-й строке и j-м столбце). ,
,  .
. 




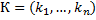 является решением системы (1), тогда этот вектор является и решением системы (2).
является решением системы (1), тогда этот вектор является и решением системы (2). является решением системы (2). Т.к. n-мерный вектор L является и решением тривиального уравнения, то он является решением системы (1).
является решением системы (2). Т.к. n-мерный вектор L является и решением тривиального уравнения, то он является решением системы (1). произвольные значения
произвольные значения  , т. е.
, т. е.  , то найдется единственное решение этой системы в виде n-мерного вектора К, у которого значения координат, соответствующих свободным неизвестным, равны соответственно
, то найдется единственное решение этой системы в виде n-мерного вектора К, у которого значения координат, соответствующих свободным неизвестным, равны соответственно 



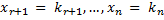 в систему (4). Тогда разрешенные неизвестные
в систему (4). Тогда разрешенные неизвестные  примут значения
примут значения  такие, что:
такие, что:


 обращает каждое уравнение системы (4) в точное числовое равенство, то он является решением этой системы. Таким образом, доказано существование решения системы (4).
обращает каждое уравнение системы (4) в точное числовое равенство, то он является решением этой системы. Таким образом, доказано существование решения системы (4). с теми же значениями свободных неизвестных является также решением системы (4). Тогда подставим его в систему (4), получим:
с теми же значениями свободных неизвестных является также решением системы (4). Тогда подставим его в систему (4), получим: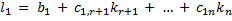


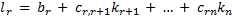
 . Таким образом, доказано, что существует единственное решение системы (4) с заданными значениями свободных неизвестных.
. Таким образом, доказано, что существует единственное решение системы (4) с заданными значениями свободных неизвестных.
 , имеет ненулевое решение. Очевидно, что
, имеет ненулевое решение. Очевидно, что  не превосходит
не превосходит  . В случае
. В случае  система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при
система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при 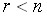 .
. , то ранг
, то ранг  , т.е.
, т.е.  . Таким образом, выполняется условие
. Таким образом, выполняется условие  с определителем
с определителем  , имеет ненулевое решение. Тогда по доказанной теореме
, имеет ненулевое решение. Тогда по доказанной теореме  вырожденная, т.е.
вырожденная, т.е.  .
. называется линейно зависимой, если система линейных уравнений (1)
называется линейно зависимой, если система линейных уравнений (1)  имеет ненулевые решения. Если же система (1) не имеет ненулевых решений, то данная система векторов
имеет ненулевые решения. Если же система (1) не имеет ненулевых решений, то данная система векторов  , что выполняется линейное соотношение (2)
, что выполняется линейное соотношение (2)  . Если же из всякого соотношения вида (2) следует, что
. Если же из всякого соотношения вида (2) следует, что 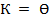 , то система векторов
, то система векторов  называется линейно независимой.
называется линейно независимой.


 (a11x10+…+a1nxn0-b1)y10+…+(am1xn0+…+amnxn0-bm)ym≥0
(a11x10+…+a1nxn0-b1)y10+…+(am1xn0+…+amnxn0-bm)ym≥0 


