
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Искусственная задача линейного программирования и ее основные свойстваСодержание книги
Поиск на нашем сайте
(1) (2) (3) xj≥0, j=1,2,…,n+1,n+2,…,n+m.
1. Вектор β=(0,…,0,b1,b2,…,bm) является опорным решением задачи (1)-(3) Заметим что по определению канонической задачи линейного программирования все координаты вектора ограничений B=(b1,b2,…,bm) должны быть неотрицательными. Так как единичные векторы E1,E2,…,Em образуют базис системы векторов условий A1,A2,…,An, E1,E2,…,Em задачи (1)-(3), то вектор ограничений В можно представить в виде линейной комбинации векторов E1,E2,…,Em с неотрицательными коэффициентами bi≥0, i=1,2,…,m, т.е. в виде B= b1 E1+b2 E2 +… + bm Em. Следовательно, по свойству базиса опорного решения вектор β=(0,…,0,b1,b2,…,bm) является опорным решением задачи (1)-(3). 2. Задача (1)-(3) всегда имеет оптимальное решение. Задача (1)-(3) имеет допустимые решения, одним из которых является например вектор β=(0,…,0,b1,b2,…,bm), так как опорное решение всегда является допустимым. Из (3) следует. Что все искусственные переменные неотрицательны, т.е. xn+i≥0, i=1,2,…,m. поэтому целевая функция (1) ограничена снизу на множестве допустимых решений. Следовательно по теореме о разрешимости канонической задачи линейного программирования задача (1)-(3) имеет оптимальное решение.
Билет №27 Теорема (о методе искусственного базиса) Пусть вектор ß=(а1, а2,…, аn, an+1, an+2,…, an+m) является оптимальным решением искусственной задачи. Тогда: 1. если an+1=an+2=…=an+m=0,то вектор а=(а1, а2,…,an) является опорным решением исходной канонической задачи линейного программирования; 2. если среди чисел an+1, an+2,…, an+m, хотя бы одно отличается от нуля, т.е. найдётся an+1>0, i=1,2,…,m, то задача не имеет ни одного допустимого решения, т.е. система ограничений канонической задачи линейного программирования является несовместной. Доказательство. Докажем первое утверждение. По условию вектор ß =(а1, а2,…, аn, an+1, an+2,…, an+m) является оптимальным решением искусственной задачи. Тогда вектор ß является опорным решением этой задачи, а, следовательно, допустимым решением и, по определению, является решением системы линейных уравнений, т.е. выполняется соотношение: A1a1+A2a2+…+Anan+E1a n+1+E2an+2+…Eman+m=B, Так как an+1=an+2=…=an+m=0, то последнее равенство можно записать в виде A1a1+A2a2+…+Anan=B. Откуда по определению следует, что вектор а=(а1, а2,…,an) является допустимым решением исходной задачи.
Так как вектор ß=(а1, а2,…, аn,0, 0,…, 0) является опорным решением искусственной задачи, то ненулевым координатам этого вектора соответствуют линейно независимые векторов условий этой задачи. Тогда некоторые из указанных линейно независимых векторов соответствуют ненулевым координатам вектора а=(а1, а2,…,an). Следовательно, вектор а является опорным решением исходной задачи. Второе утверждение теоремы будем доказывать от противного, предположив, что существует число аn+i >o, i=1,2,…,m, но при этом исходная задача имеет допустимое решение а=(k1,k2,…kn), которое удовлетворяет системе и kj≥, j=1,2,…,n. Тогда по определению допустимого решения выполняется соотношение: A1k1+A2k2+…+Ankn=B, которое можно переписать в виде A1k1+A2k2+…+Ankn+A n+10+An+20+…An+m0=B. Откуда следует, что вектор ß’=(k1, k2,…, kn,0, 0,…, 0) является допустимым решением искусственной задачи. Так как по условию вектор ß=(а1, а2,…, аn, an+1, an+2,…, an+m) является оптимальным решением искусственной задачи, то φ(а=(k1,k2,…kn),) ≤ φ(ß’), что равносильно неравенству: a n+1+an+2+…an+m≤0+0+…0. Однако, по предположению, существует a n+1>0, i=1,2,…,m, а следовательно, a n+1+an+2+…an+m>0. Получено противоречие. Таким образом, предположение о существовании допустимого решения исходной задачи является неверным. Следовательно, система ограничений исходной задачи является несовместной.
Билет №28 Основные свойства взаимно двойственных задач ЛП 10. если векторы а=(k1,…kn) и ß=(l1,…,lm) являются допустимыми решениями взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно, то f(a)≤φ(ß). Доказательство. Значение целевой функции ЗЛП (1)-(4) на допустимом векторе а=(k1,…kn) с учетом доказанной леммы можно записать в виде f(a)=y1k1+…+yTkn+y0≤(∑i=1mai11j)k1+…+(∑mi=1ain1j)kn+y0=(a1111+…+am11m)k1+…+(a1n11+…+amn1m)kn+y0= (a11k1+…+a1nkn)11+…+(am1k1+…+am1kn)1m+y0=(∑j=1na1jkj)11+…+(∑j=1namjkj)1m+y0=b111+…+bm1m+y0≤φ(ß). Следовательно, f(a)≤φ(ß).
20. Если векторы а0 и ß0 являются допустимыми решениями взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно, и f(a0)=φ(ß0), то векторы а0 и ß0 – оптимальные решения этих задач соответственно. Доказательство. Для произвольного допустимого решения а задачи ЛП (1)-(4) по свойству 10 выполняется неравенство f(a)≤φ(ß0).так как по условию f(a0)= φ(ß0), то f(a)≤f(а0) и по определению вектор а0 является оптимальным решением ЗЛП (1)-(4).
Оптимальность вектора ß0 доказывается аналогично.
30. Если целевая функция одной из взаимно двойственных задач ЛП неограниченна на множестве допустимых решений этой задачи, то другая взаимно двойственная задача ЛП не имеет ни одного допустимого решения, т.е. система условий этой задачи является несовместной. Доказательство. Доказательство проведем от противного. Пусть целевая функция - φ(ß) задачи ЛП (1’)-(4’) неограниченна снизу на множестве допустимых решений, а задача ЛП (1)-(4) имеет допустимое решение –а. тогда по свойству 10 для любого допустимого решения-ß задачи ЛП (1’)-(4’) должно выполняться неравенство f(a)≤φ(ß). Это неравенство противоречит неограниченности снизу целевой функции φ(ß) на множестве допустимых решений этой задачи. Следовательно, задача ЛП (1)-(4) не имеет ни одного допустимого решения, т.е. система условий этой задачи несовместна.
Билет №29 Теоремы двойственности Теорема 1. Если одна из взаимно двойственных задач ЛП имеет оптимальное решение, то и другая взаимно двойственная задача ЛП имеет оптимальное решение, при этом значения целевых функций на оптимальных решениях этих задач совпадают. Если же целевая функция одной из взаимно двойственных задач ЛП неограниченна на множестве допустимых решений, то вторая из взаимно двойственных задач ЛП не имеет ни одного допустимого решения, т.е., система условий второй задачи несовместна. Доказательство теоремы следует из сформулированных выше свойств. Теорема 2. Пусть векторы a0=(x10,…,xn0) и ß0=(y10,…,ym0) являются допустимыми решениями взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно. Для того, чтобы векторы a0 и ß0 были оптимальными решениями этих задач необходимо и достаточно выполнение следующих равенств: { xj0(∑mi=1aijyj0-yj)=0, j=1,2,…,n; {yi0(∑nj=1aijx0j-bi)=0, i=1,2,…,m. Доказательство. Необходимость. Пусть векторы a0 и ß0 оптимальные решения взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно. Тогда по свойству 20 выполняется равенство f(a0)=φ(ß0), которое можно записать в виде: y1x10+…+ynxn0+y0=b1y10+…+bmym0+y0. Это равенство с учётом соотношения (∑aijyi0)xj0≥yjxj0,j=1,2,…,n,равносильно неравенству: (∑ai1yi0)x10+…+(∑aiTyi0)xT0≥b1y10+…+bmym0 В то же время, из условий задач (1)-(4) и (1’)-(4’) следует, что каждое слагаемое в последнем неравенстве неположительное. Поэтому и все выражение в левой части этого неравенства должны быть не положительны. Следовательно в последнем отношении должно быть равенство, т.е. (∑a1jxj0-b1)y10+…+(∑amjxj0-bm)ym0=0. Однако сумма положительных слагаемых может равняться нулю только тогда, когда каждое слагаемое равно нулю. Таким образом, необходимость для выполнения второго соотношения в утверждении теоремы доказана. Необходимость для выполнения первого соотношения в утверждении теоремы доказывается аналогично. Достаточность. Пусть выполняются равенства: { xj0(∑mi=1aijyj0-yj)=0, j=1,2,…,n; {yi0(∑nj=1aijx0j-bi)=0, i=1,2,…,m. Тогда f(a0)=y1x10+…+ynxn0+y0=xj0(∑aijyi0)+…+xj0(∑aijyi0)+y0=(a11y10+…+am1ym0)x10+…+(a1ny10+…+amnym0)xn0+y0= =b1y10+…+bmym0+y0=φ(ß0)
Т.е. f(a0)= φ(ß0). Откуда с учётом свойства 20 следует, что векторы a0 и ß0 оптимальные решения взаимно двойственных задач ЛП (1)-(4) и (1’)-(4’) соответственно.
Билет №30
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.162 (0.01 с.) |

 (X)=xn+1+xn+2+…+xn+m(min)
(X)=xn+1+xn+2+…+xn+m(min)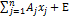 1xn+1+E2xn+2+…+Emxn+m=B
1xn+1+E2xn+2+…+Emxn+m=B (a11x10+…+a1nxn0-b1)y10+…+(am1xn0+…+amnxn0-bm)ym≥0
(a11x10+…+a1nxn0-b1)y10+…+(am1xn0+…+amnxn0-bm)ym≥0 


