
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 1. Вычислить логарифмы констант равновесийСодержание книги
Поиск на нашем сайте
(1)Al(OH)3↓ + (j-3) OH-D Al(OH)j3-j , для j = 1-4; (2) Zn(OH)2↓ + (j-2) OH-D Zn(OH)j2-j, для j = 1-4; (3) Fe(OH)3↓ + (j-3) OH-D, Fe(OH)j3-j, для j = 1-4; (4) Ni(OH)2↓ + (j-2) OH-D Ni(OH)j2-j, для j = 1-4; (5) Cu(OH)2↓ + (j-2) OH-D Cu(OH)j2-j, для j = 1-4; (6) Cd(OH)2↓ + (j-2) OH-D Cd(OH)j2-j, для j = 1-4; (7) AgOH↓ + (j-1) OH-D Ag(OH)j1-j, для j = 1-2. Упражнение 2. Найти линейные комбинации реакций и величины логарифмов их констант ЗДМ, объясняющие такие наблюдения: 1) AgCl(s) растворяется в водной NH3; 2) PbSO4(s) растворяется в растворе NaOH; 3) BaSO4(s) превращается в BaCO3(s) действием раствора Na2СO3; 4) синий раствор Cr(OH)4 переходит в желтый действием H2O2 в щелочной среде; 5) BiI3(s) дает желто-оранжевый раствор с избытком раствора KI; 6) HgI2(s) дает желто-оранжевый раствор с избытком раствора KI; 7) белый осадок Bi(OH)3(s) переходит в черный действием раствора SnCl2 в среде HCl; 8) из раствора Hg(NO3)2 выпадает серый осадок действием раствора NH2OH×HCl в смеси HCl и избытка водяного NH3; 9) из раствора Hg (NO3)2 выпадает серый осадок действием раствора H2O2 в смеси HCl и избытка водяного NH3; 10) Cu(OH)2(s) растворяется в водной NH3; 11) из смеси растворов Cu(NO3)2 и KI выпадает окрашенный осадок, а из раствора можно удалить I 2 в растворитель СCl4, не смешивается с водой и I2 в котором дает фиолетовый раствор. Упражнение 3. Вычислить рН растворов: 1) фосфорной кислоты, H3PO4, если c (H3PO4) =0,010 моль/л; 2) гидрогенсульфида (сероводородной кислоты), H2S, если c (H2S) = = 0,10 моль / л; 3) раствора CO2 (угольной кислоты), c (CO2)=0,10 моль/л; 4) раствора SO2 (сернистой кислоты), c (SO2)=0,10 моль/л; 5) лимонная (лимонной) кислоты, C6H8O7, или H3L, c (H3L)= =0,010 моль/л; 6) аммиака, NH3, если c (NH3)=0,010 моль/л; 7) метиламина, CH3NH2, c (CH3NH2)=0,010 моль/л; 8) пиридина, C5H5N, c (C5H5N) = 0,010 моль / л; 9) ацетата натрия (сильной соли), NaAc, c (Na+) = c (Ac-)=0,010 моль/л; 10) формиата натрия (сильной соли), c (Nа+) = c (НСОО-)=0,010 моль/л. Упражнение 4. Вычислить по балансу реакций растворимость в воде, учитывая кислотно-основные преобразования: (1) Ag2CO3↓+H2O D AgOH +HCO3-; (2) Ag3PO4 ↓+3H2O D 3AgOH +HPO42-+2H+; (3) BaCO3 ↓+H2O D Ba2+ + HCO3-; (4) PbCO3 ↓+H2O D Pb(OH)+ + HCO3-; (5) ZnS (b)↓+H2O D Zn(OH)+ + HS-; (6) CaSO3 ↓+H2O D Ca2+ + HSO3-; (7) FeS ↓+H2O D Fe(OH)+ + HS-; Упражнение 5. К раствору, содержащему смесь катионов: 1) (Ag+, Ca2+, Pb2+) с концентрацией 0,01 моль/л добавляют анион-осадитель - карбонат (CO32-) 2) 2) (Ag+, Cu2+, Sr2+) с концентрацией 0,01 моль/л добавляют анион-осадитель - карбонат (CO32-) 3) 3) (Ag+, Hg22+, Pb2+) с концентрацией 0,01 моль/л добавляют анион-осадитель - хлорид (Cl-) 4) 4) (B2+, Sr2+, Ca2+) с концентрацией 0,01 моль/л добавляют анион-осадитель - фторид (F-) 5) 5) (Ag+, Ba2+, Ca2+) с концентрацией 0,01 моль/л добавляют анион-осадитель - сульфит (SO32-) 1. Какой из катионов будет осаждаться первым, вторым, третьим? 2. Укажите концентрации всех катионов на момент начала осаждения каждого из них. Упражнение 6. Вычислить концентрацию иона: (1) [Fe3+] в 0,01 моль/л раствора FeCl3, к которому было добавлено 0,1 моль KCNS; (2) [Cd2+] в 0,01 моль/л раствора Cd(NO3)2, к которому было добавлено 0,1 моль KCN; (3) [Ni2+] в 0,1 моль / л раствора Ni(NO3)2, к которому было добавлено 1,0 моль NH3; (4) [Cu2+] 0,05 моль / л раствора Cu(NO3)2, к которому было добавлено 1,0 моль NH3; (5) [Hg2+] в 0,1 моль / л раствора Hg(NO3)2, к которому было добавлено 1,0 моль KI.
КОЛИЧЕСТВЕННІЙ АНАЛИЗ
Теория погрешностей и статистическая обработка При проведении экспериментальных исследований изме-вания повторяют несколько (n) раз - получают параллельные зна-чение измеряемого параметра: x1. x2... xn; (n - число параллель ных измерений). Эти значения близки, но не совпадают, они отличаются друг от друга. Разницу между измеренным значением x i и действительным x real называют абсолютной погрешностью измерения или «абсолютным отклонением»: Δ xi = |xi- xreal.| (1) Поскольку отклонения x i от x real может быть со знаком «+» или «-» абсолютную погрешность вычисляют по модулю (абсолютным значением). Каждый параллельный опыт имеет свою характерным. абсолютную погрешность. Чтобы найти относительную погрешность, надо абсолютную разделить на значение измеряемой величины: Δ xвідн .= Δ x/ xreal ≈ Δ x / xi. (2) Погрешности бывают случайные и систематические. Случайная погрешность - это составляющая погрешности измерения, что изменяются случайным образом при повторных измерениях одной и той же величины. Случайные погрешности обязаны своим происхождением ряду причин, действие которых неодинакова в каждом опыте и не может быть учтена. Они имеют разные значения даже для измерений, выполненных одинаковой. Систематическая погрешность - это составляющая погрешности измерения, что остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Совокупность измеренных значений одного и того же параметра - это выборка или ряд. Если измеренные значения расположены по рангу (по возрастанию ряд X1<X2<... <XN. Или ниспадающий X1> X2>...> XN). такой ряд называют ранжированы рядом. Разность между наибольшим и наименьшим значениями ре-результатов наблюдений называют размахом варьирования (w= xmax - xmin). В растущем ранжировом ряду это - w = X N - X 1. Статистическую обработку результатов измерений начинают с проверки соответствия данных выборки функциональной зави-ности нормального распределения данных. В некоторых случаях оказывается, что результат одного измерения резко отличается от результатов других измерений, использованно при тех же контролируемых условиях. В этом случае говорят о грубой ошибку (промах в измерении). Для выявления грубых промахов в выборке известно несколько различных статистических критериев. Самый среди них Q-критерий. Для проверки крайних значений в ранжированных ряде рассчитывают значение Qексперимент (3) и сравнивают с табличным значением Qтабл (n, P) (см. Табл.1), где n - число параллельных измерений в выборке, Р - доверительная вероятность. В аналитической химии принято использовать доверительную вероятность Р = 0,95. В биологии, медицине чаще используют доверительную вероятность Р = 0,99.
Если в выборку попадает значение с большой погрешностью X1 или Xn - это измеренное значение удаляют из выборки и при статистичний обработайте не учитывают. Действительным значением измеряемой величины, если оно неизвестно к измерениям, считают среднее арифметическое из па-лельно значений измерений.
Таблица 1
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.107 (0.009 с.) |

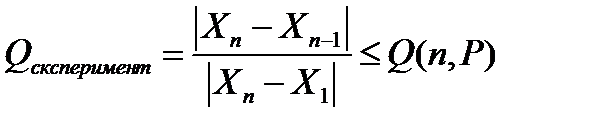 ;
;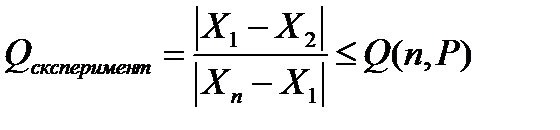 . (3)
. (3)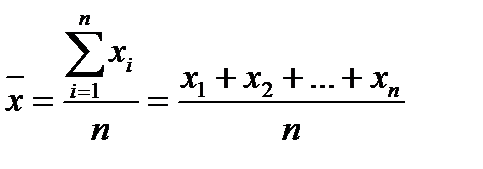 . (4)
. (4)


