
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование органических реагентов в анализеСодержание книги
Поиск на нашем сайте
5. ЗАКОН ДЕЙСТВИЯ МАСС. АЛГЕБРА Химическое равновесие. Обратные реакции проходят как в прямом, так и в обратном направлениях. Равновесие устанавливается, если эти изменения взаемокомпенируется. Равновесный состав - совокупность равновесных концентраций в состоянии равновесия. Их обозначают формулами реагентов, взятые в квадратные скобки, например [H+], [H3PO4], [OH‑], [PO43‑]. С курса общей химии известно, что скорость химической aA + bB DcC + dD, (1)
Следует знать, что выражение константы равновесия через равновесные концентрации (концентрационного константы) сбывается при постоянной ионной силе раствора(I). Ионная сила выступает обобщенной степени ионности раствора, и ее рассчитывают по уровнению:
Произведение равновесной концентрации ([Az±]) и квадрата При переменной ионной силе раствора константа равновесия остается неизменной, если вместо равновесных концентраций в выражении (3) использовать активность (ai) участников равновесия:
Константу равновесия, выраженную через активности называют термодинамической константой aAi = γ Ai ·[ Aiz ] (6) где γ Ai - коэффициент активности иона А±z. Значение коэффициента активности можно оценить с варианта приближения уравнения Дебая-Хюккеля, предложенный Дэвисом.,
Для большинства химических реакций, используемых в аналитической химии значения констант равновесия измерен в специальных физико-химических исследованиях. Данные таких исследований сведены в справочной литературе. Константы при температуре, отличающейся от стандартной, 25°С, определяют по формуле lg K (t oC) = lg K (25oC) + 5,88×10‑4×D H (t – 25), где D H - энтальпия реакции,кДж/моль. Формула является приближенной, поскольку полученная интергрированием уравнение Вант Гоффа при постоянных теплоемкости реагентов. Для многих реакций коэффициент D H, что Реакции в растворах, которые могут проходить как в прямом, так и в обратном направлениях еще называют «равновесия». Известны равновесия - кислотно-основные, осаждения-растворения, окислениие-восстановления, комплексообразования. Обозначения констант в справочной литературе. Константы определяют экспериментально и приводят в справочной литературе. Различая их, по рекомендациям ИЮПАК (International Union of Pure and Applied Chemistry), в скобках после K записывают реакции, как аргумент функции, например,
K (H2O D H+ + OH‑), K (H3PO4 D 3 H+ + PO43‑). Сокращая обозначения, используют две буквы - K и b - с индексами (табл. 3). Первый индекс - тип реакции. Он отсутствует для комплексообразования; буква H - присоединение H+ к основам, буква a («acidity», кислотность) - отщепление H+ кислотами, буква s («solubility», растворимость) для растворимости, буква D («distribution», распределение) - распределение вещества между двумя растворителями. Дальнейшие индексы указывают состав продукта. В примерах табл. 3: M - комплексообразователь, сокращение от «металл», L - лиганд, а также и в записи кислотно-основных преобразований, поскольку типичные лиганды являются основами Бренстеда. Обозначение сокращают. Так, b62 для реакции Ag+ с I‑ не связывают с AgI6261‑, невероятного состава и строения, а понимаем индекс как двойной, что соответствует Ag2I64‑. Определение констант равновесий приведены в табл. 3. Ниже рассмотрим примеры для часто используемых констант. Кислотно-основные равновесия - это реакции обмена, в которых принимают участие протоны Н+. Ионы водорода могут вступать в реакцию или образовываться в результате взаимодействия других соединений. К кислотно-основным равновесий относят автопротолиз растворителя, равновесия протонирования и диссоциации.
Равновесие диссоциации воды:
Равновесия ступенчатого протонирования (ступенчатые равновесия протонирования) слабого основания (например, аммиака), или аниона слабой кислоты (например, сульфитной). Прикрепленный первого протона: NH3+H+DNH4+
SO32-+H+D HSO3-;
Присоединение второго протона: HSO3-+H+D H2SO3;
HNO2 D H++NO2- Ka1= Обращаем внимание, что константы диссоциации и протонирования для одной и той же соединения связаны между собой. Так, для одной-сновным кислоты на: Ka1(НА) = 1/KH1(А-) = KH1-1; для двухосновной кислоти Н2А: Ka2(Н2А) = 1/KH1(А2-) = KH1-1. Для многоосновной кислоты НaА: Ka1(НaА) = 1/KHa(Аa-) = KHa-1. • присоединение трех протонов - РO43-+3H+D H3РO4 βН3 = КН1·КН2·КН3; РO43-+2H+D H2РO4- βН2 = КН1·КН2; РO43-+H+D H2РO42- βН1 = КН1. Равновесия осаждения-растворения - это реакции, в которых вы необходимость вещество находится в одной фазе (твердой, кристаллической), а продукты - в другой (жидкостной). Например, растворимость хлорида серебра в воде характеризует константой «произведение растворимости»: AgCl ↓DAg+ + Cl- Ks= [Ag+]· [Cl-]=1,78·10-10=10-9,75. Обратную реакцию - образование осадка, осаждение - характеризуется ют константой Ks-1. Равновесия окисления-восстановления - это реакции, в которых атомы участников меняют степень окисления. Поскольку при прохождении таких реакций один участник теряет электроны (окисливается), а другой их присоединяет (восстанавливается) - любую окислительно-восстановительную реакцию можно рассматривать как объединение акцепторной и донорной полуреакций:
В справочной литературе все реакции с изменением степени окисления рассматриваются одинаково, как акцепторные. Поэтому для донорных полуреакций берут обратное значение константы. Константу окислительно-восстановительной реакции находят путем суммирования левых и правых частей двух полуреакций с дополнительными стехиометрическими коэффициентами: m(Ox1 + n e - )+n(Red2- m e -) D mRed1 + nOx2; (11) Равновесие реакции MnO4-+5 Fe2+ +8h+ D Mn2+ +5 Fe3+ +4h2o. Запишем уравнения полуреакций: 1) MnO4-+8h+ +5 e -D Mn2+ +4h2o k1 = 10127,5. 2 Fe2+ - e - D Fe3+ K2-1 = 10-13,0. Константа равновесия k = k1·К2-5 = 10127,5+5(-13,0) = 1062,5. Для характеристики равновесий комплексообразования ис-пользуют ступинасти константы образования комплексов (К), общие константы образования комплексов (βі), константы дисоциации комплексных соединений (ki). Ступенчатая равновесие присоединения третьей молекулы Cu(NH3)22+ + NH3 D Cu(NH3)32+ K3 = β3/ β2 =1010,27/107,47 = 102,8. Cu2+ + 4NH3 D Cu(NH3)42+ β4 = K1·K2·K3·K4 = 1011,75. Fe3+ +6CN- D Fe(CN)63- β6= 1043,6.
CdI42- D CdI3-+I- k1 = β3/β4=105/106 = 0,1. Равновесие ступенчатой диссоциации по третьей степени иодидних комплексов кадмия (отщепление третьего йодида) CdI22- D CdI+ + I- k3= β1/β2 =102,28/103,92 =101,64. Алгебраический подход при записи уравнений Рассмотрим реакцию общего вида 0 D 0D - aA – bB+ cC + dD. (13) К примеру, H2O D H+ + OH‑ переходит в 0 D ‑ H2O + H+ + OH‑, H3PO4 D 3 H+ + PO43‑ - в 0 D ‑ H3PO4 + 3 H+ + PO43‑. Условия равновесия зададим законом действия масс (ЗДМ), где П - символ произведения, aj - активность реагента A j, K – константа равновесия. ЗДМ для реакции (13) [A]-a·[B]–b·[C]c·[D]d = K. На константу равновесия влияет много факторов, например, температура. Активность растворителя, H2O (в разбавленных растворах), как и химических индивидов, образующих отдельную фазу (твердую или жидкую), не включаются в записи ЗДМ, считая их равными 1. Так, для реакции
Ca5(OH)(PO4)3(s) D 5 Ca2+ + OH- + 3 PO43- Активность твердой фазы не включаем в запись ЗДМ, { a (Ca2+)}5 a (OH-) { a (PO43-)}3 = K. Для реакции ЗДМ имеет вид чтобы упростить индексы, активности обозначено буквой a с химической формулой реагента в скобках. Активность a (H2O) = 1 в запись не вводим. Если не принимать отрицательных стехиометрических коэффициентов, то левую часть (2) записывают как отношение двух произведений с положительными степенями, в числителе - для продуктов, в знаменателе - для исходных реагентов, Таблица 4 Обозначение констант равновесий
1. Константы стойкости комплексов
2. Константы кислотно-основных равновесий (продолжение)
Концентрационные константы. Константу равновесия, выраженную через равновесные концентрации (3) называют концентрационнной. Подставляя выражение (6) в ЗДМ (3), приходим к его аналогу с равновесными концентрациями вместо активностей, Или следуя алгебраического подхода в записи реакций и уравнений, имеем:
lg K c = lg K - Концентрационная константа равновесия K c зависит от состава раствора через g j. Часто пользуясь K c, а не указывать индекс «c». В справочниках приводят термодинамические (при I = 0), так и концентрационные константы. Примерно оценивая ионную силу, ограничиваемся вкладом от преобладающих компонентов, в частности ионов сильных электролитов (тех, что диссоциированных полностью). Исследуя константы, из сильных электролитов образуют так называемый «солевой фон», который стабилизирует коэффициенты активности. В водных растворах сильнымы есть кислоты HCl, HClO4, HBr, HI, H2SO4 (по первой ступенью диссоциации), HNO3; основания и соли с катионами Na+, K+, Rb+, Cs+ не склонен к комплексообразованию, и соли с анионом ClO4‑. Равновесные концентрации рассчитывают по концентрационными константами, прибегая к итераций (последовательных приближений). Рассчитав [A j ] за lg K c, что отвечают приближенной ионной силе, уточняют I и lg K c, и снова [A j ]. Процесс заканчивают, если значение lg K c отличаются от предыдущих в пределах погрешностей. Итерации сходятся, потому что lg K c медленно изменяются с [A j ]. Например, для реакции Ca5(OH)(PO4)3(s) D 5 Ca2+ + OH- + 3 PO43-, lg Ks = ‑55,91 [ I =0], lg Ks c в бреде c (NaClO4) = 0,1 моль/л вычисляем. Электролит NaClO4 – сильный, [Na+] = [ClO4‑] = c (NaClO4) = 0,1 моль/л. Без взноса от продуктов реакции ионная сила I = {[Na+] + [ClO4‑]} / 2 = 0,1. По формуле Девиса lg g = ‑ 0,5 Подставляя ее в выражение (6), имеем lg Ks с = lg Ks ‑ {
+ 1·(‑1)2 + 3·(‑3)2}·(-0,105) = ‑55,91 + 30·0,105 = -52,76. Линейные комбинации реакций Мы уже имели возможность обратить внимание, что уравнение присоединения нескольких протонов в многозарядного аниона (или нескольких лигандов к иону-комплексообразователя) характеризуются общей константой, равной произведению ступенчатых констант: β βn = K·K·…·Kn Аналогичным образом можно вычислить константу более сложного равновесия, используя константы простых равновесий. Пример 1. Рассмотрим равновесие растворения малороз-действующей соли слабой кислоты в растворе сильной кислоты. CaCO3↓ + 2H+ D Ca2+ + H2O + CO2; K-? Решение. Реация состоит из двух простих равновесий: CO32- +2H+DH2O+CO2; βH2=KH1·KH2=1010,33· 106,35=1016,68 Значит константа равновесия исходной реакции: K= Ks βH2=10‑8,52 ·1016,68=108,16; Ответ: K=1,45·108. Пример 2. Равновесие растворения малорастворимого гидроксида в растворе аммиака: Cu(OH)2↓ +4NH3 DCu(NH3)42++2OH- K=? Решение. Исходным веществом осадок гидроксида, значит первой равновесием следует рассмотреть равновесие растворения: Cu(OH)2↓D Cu2++2OH Ks = 10-19,32. Ионы Cu2+, образовавшиеся взаимодействуют с молекулами аммиака: Cu2+ + 4NH3 D Cu(NH3)42+ β4 =1011,75. константа равновесия выходной реации: Ответ: K = 2,69·10-8. Пример 3. Равновесие образования осадка при разрушении комплексного соединения BiI4-+PO43- D BiPO4↓ + 4I-. Решение. Исходными являются комплексные анионы, значит первой равновесием следует рассмотреть равновесие диссоциации: BiI4- D Bі3+ + 4I- β4-1 = 10-15. Ионы Bi3+, образовавшиеся взаимодействуют с анионами фосфата Bі3+ + PO43- D BiPO4↓ Ks-1 = 1022. Константа равновесия выходной реакции: K= β4-1· Ks-1 =10-15·1022,9 = 107,9; Ответ: K = 7,94·107. Теоретически изучая равновесные системы, учитываем ЗДМ для различных реакций. Вместо того, чтобы превращать алгебраические прримеры ЗДМ, нагляднее превратить реакции, для которых справочные данные, переходя к линейным комбинаций реакций. Рассмотрим выходные реакции 0 D S a ij A j, (16) где i - номер реакции, a ij - стехиометрический коэффициент в i -й реакции при реагенте A j. Умножая реакции на множители k i и добавляя произведения, образуем линейную комбинацию 0D S (S ki a ij) A j, (17) с стехиометрическими коэффициентами - линейными комбинациями коэффициентов выходных реакций. Логарифмируя уравнения ЗДМ для реакции (7), имеем S a ij lg aj = lg Ki, где Kі - константа ЗДМ для i -й реакции; a j - активность реагента A j. Создавая линейную комбинацию этих уравнений, имеем (S ki a ij) lg aj = S lg Ki = lg K, (18) где K - константа ЗДМ линейной комбинации (то есть реакции 8). Не усложняя уравнений ЗДМ, k i выбираем так, чтобы коэффициенты (S ki a ij) при некоторых реагентах вращались на 0 (реагенты «сокращались»), и соответствующая активность в ЗДМ не входила. Комбинируя n реакций, «сокращаем» по крайней мере (n - 1) реагентов. Линейная комбинация удовлетворяет требованию, число атомов каждого элемента в реакции сохраняется, потому что ей удовлетворяют выходные реакции. Линейно независимы реакции - такие, что ни одна из них не является линейной комбинацией других. Математические термины «линейная комбинация» и «линейная независимость» соответствуют структуре множества реагентов и реакций. ЗДМ для независимых реакций являются независимыми алгебраичными уравнениями. Зависимым реакции соответствуют зависимые уравнения ЗДМ. Рассмотрим наиболее часто линейные комбинации. H+ + C2O42‑ D HC2O4‑, lg K H1 = 4,266, H+ + HC2O4‑ D H2C2O4, lg K H2 = 1,252. Реакции кислотной диссоциации - обратные приведенным: H2C2O4 D H+ + HC2O4‑, lg Kа 1 = ‑ lg K H2 = ‑ 1,252, HC2O4‑ D H+ + C2O42‑, lg Kа 2 = ‑ lg K H1 = ‑4,266. Нумерация констант также обратная. Для констант устойчивости ее начинают от основания Бренстеда, C2O42‑, второй индекс при lg K H і и соответствует номеру иона Н+, что присоединяется к C2O42‑. Для констант кислоты диссоциации ее начинают от H2C2O4, второй индекс при lg Kаі соответствует номеру иона Н+, отщепляется от Н2C2O4. Переход от логарифму константы одного типа к другому - это просто изменение знака (умножение на -1, то же множитель, на который умножаем реакцию). Это следует из уравнений ЗДМ. так, lg a (HC2O4‑) ‑ lg a (H+) ‑ lg a (C2O42‑)} = lg K H2, lg a (H+) + lg a (C2O42‑) ‑ lg a (HC2O4‑) = lg Ka 1 = ‑ lg K H2. Второй типичный случай - переход между общими и ступенчатыми константами. Так, для Zn2+ и NH3 имеем
Здесь реакции подано «в столбик», слева - множители k i. Советуем пользоваться подобной наглядной форме записи. Простота перехода к константе обратной реакции ведет к более удобного записи рассматриваемой линейной комбинации:
С ЗДМ следует переход к константе линейной комбинации, lg a (Zn(NH3)32+) – lg a (Zn2+) – 3 lg a (NH3) = lg b3, lg a (Zn(NH3)22+) – lg a (Zn2+) – 2 lg a (NH3)} = lg b2, lg a (Zn(NH3)32+)–lg a (Zn(NH3)22+) – 3 lg a (NH3)3} = lg K 3 = lg b3–lg b2. Легко обобщить этот результат, lg Kі = lg b і ‑ lg b(і – 1), lg b і = Приведем еще примеры. Для реакции с участием иона металла Zn2 + имеем Zn2+ + і Н2О D Zn(ОН) і 2 ‑ i + і Н+, lg *b і = lg b і + і lg Kw, где b і - общая константа устойчивости гидроксокомплексы, а Kw - константа автопротолизу воды. Для реакции твердой фазы с образованием комплексов собственного аниона, например, Hg2+ із I‑,, имеем HgI2(s) + (i – 2) I‑ D HgI i 2 – i , lg Ksi = lg Ks 0 + lg b i, где Ks0 - произведение растворимости HgI2 (s), HgI2(s) D Hg2+ + 2 I‑, lg Ks 0 = ‑24,07 [ I = 0,5], b i - общая константа устойчивости продукта - водного комплекса ртути, Hg2+ + i I‑ D HgI i 2 ‑ i , lg b i = 12,87 (i = 1); 23,82 (i = 2); 27,6 (i = 3); 29,8 (i = 4) [ I = 0,5].
При i = 1 стехиометрический коэффициент (i – 2) является отрицательным, но мы уже привыкли относиться к реагентам так же, как к членам алгебраических уравнений, перенося их из одной части уравнения в другую с обратным знаком. Коэффициент (-1) слева означает, что соответствующий реагент является продуктом реакции. Приведем запись в столбик для реакций, продуктом которых является последний комплекс,
Экономя объем справочников, не приводя реакций, непосредственно отражают конкуренцию между различными лигандамы за комплексообразователь, или между различными комплексообразователями за лиганд. Множество таких комбинаций можно составить из имеющихся реакций, изучая, например, маскировки. С подобной проблемой мы встречаемся, изучая обмен не лигандамы, а электронами, в окислительно-восстановительных реакциях. В справочной литературе обычно подают сведения об условиях равновесия для так называемых полуреакций, с участием окисленной и восстановленной форм и свободных электронов nOx Ox + ne e- D nRed Red, (19) n с соответствующими индексами - стехиометрические коэффициенты. Конечно, другие участники реакции кроме Ox и Red также должны входить в уравнения (10). lg K = ‑ne k E 0. (20) Формой ЗДМ для полуреакций есть уровнение Нернста, = E 0 − (k E 0 / ne) (nRed lg a Red − nOx lg a Ox), (21) k = F / (2,3 RT), где E - окислительный потенциал, k - множитель Нернста, F - постоянная Фарадея, R - газовая постоянная, T - абсолютная температура, связывает потенциал полуреакции с логарифмом ее константы. При 273,15 К (25°С) коэффициент k равен 0,0591В. Окислительный потенциал соответствует логарифм активности электрона lg a e = ‑ E / k. (22) Чем потенциал больше, тем больше способность формы Ox выступать в качестве окислителя. Чтобы вычислить логарифм линейной комбинации полуреакций, логарифмы констант полуреакций удобнее потенциалы. Если реакцию (10) разделить на стехиометрический коэффициент при электроне, ne, (nOx / ne) Ox + e‑ D (nRed / ne) Red, в ней примут участие (nOx / ne)Ox и (nRed / ne) Red, эквиваленты окисленной и восстановленной формы. Множитель при E 0 в формуле (11) отсутствует. В качестве примера, рассмотрим действие H5IO6 на Mn2+. известны полуреакции MnO4‑ + 8 H+ + 5 e‑ D Mn2+ + 4 H2O, 127,5, H5IO6 + H+ + 2e‑ D IO3‑ + 3 H2O, 54,0. Запишем первую в обратном направлении, чтобы не употреблять отрицательных коэффициентов,
В какую сторону смещен равновесие реакции? Рассмотрим выражения ЗДМ и с аналогичной для концентрационного константы. Чем больше есть константа ЗДМ, тем больше величины для продуктов реакции (с положительными показателями степени) и тем меньше величины для выходных реагентов реакции (с отрицательными показателями). Если константа очень большая, то равновесие реакции смещено вправо, в сторону продуктов, а если очень мала, то влево, в сторону исходных веществ. Например, решая, в какую сторону смещен равновесие реакции взаимодействия уксусной кислоты с аммиаком, рассмотрим линейную комбинацию реакций
с которой изъято ионы Н+. Большая константа линейной комбинации, К = 105,52, свидетельствует о смещении равновесия вправо. Рассмотрим, может Ag2CrO4(s) заметно растворяться в водном NH3. Составим линейную комбинацию реакций, с которой изъято ион Ag+.
Константа достаточно большая, так что можно надеяться на заметный сдвиг реакции справа и растворения Ag2CrO4(s).
Поскольку константа большая, на первый взгляд, можно действием NH3 почти полностью перевести NH |




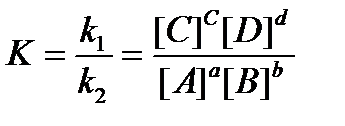 (3)
(3) (4)
(4) (5)
(5) , lg g z ± = z 2 lg g1± (7)
, lg g z ± = z 2 lg g1± (7)
 .
.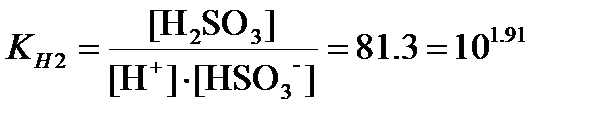 .
. .
.
 (10)
(10)
 a j A j, (12)
a j A j, (12) = K, (14)
= K, (14) = К.
= К.
 , Br2 D Br2(CCl4), або Br2 D
, Br2 D Br2(CCl4), або Br2 D 

 = K c = K · (
= K c = K · ( )-1,
)-1, lg (
lg ( ) = lg K –
) = lg K –  a j lg g j. (15)
a j lg g j. (15) / (1 +
/ (1 +  ) + 0,15 I = -0,105.
) + 0,15 I = -0,105. lg Kj .
lg Kj .


