
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значение t-критерия СтьюдентаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример 1. При определении массовой доли ионов цинка (II) в крупе были получены следующие результаты: 0,230; 0,239; 0,237; 0,235; 0,237 мг/кг. Сделать статистическую обработку результатов измерений. Решение: Сформируем ряд по рангу: 0,230, 0,235, 0,237, 0,237, 0,239. Проверим крайние значения на возможные погрешности (см. Уравнение (3)):
Это значит, что наибольшее и наименьшее значение в ряду, что измерили, не является погрешностями. Вычислим среднее значение (см. уравнение (4)):
И в завершение вычислить доверительный інтервал
Ответ: Результат анализа крупы выражается доверительным интервалом вокруг средней величины: [0,232-0,240], или ω = 0,236 ± 0,004.
Одна из задач, которую можно решить с использованием статистически методов - это задача о возможности объединения двух выборок, полученных в различных условиях. Например, одну и ту же характеристику - массовую долю компонента в объекте, измерен двумя различными методами: x11, x12, x13,..., x1n; x21, x22, x23,..., x2m. Можно объединить выборки в одну, которая имеет n + m значений? Решением такой задачи предполагает ответы на два зап-ния: -есть ли выборки однородные (выполнены с одинаковой точностью)?
- или выборки не содержат систематических погрешностей? Чтобы ответить на эти вопросы вычисляют среднее зна-чение для каждой выборки Соотношение большей дисперсии к меньшей сравнивают с статистически критерием Фищера-F(n2 - 1, n1 - 1, P) (см. Таблицу 4).
Если соотношение экспериментальных дисперсий не превышает значения критерия Фишера это значит, выборки одно- родные, а значение равноточными. Для проверки возможной систематической погрешности по уравнениям(11) исследуют различия между средними значениями двух выборок. Отношение этой разницы к средневзвешенному стандартных отклонений (s12) не должно превышать -критерий Стьюдента.
Выполнение условий по уравнениям (9) и (11) позволяют объединить две выборки и вычислить для новой объединенной выборки среднее значение и стандартное отклонение. Пример 2. Определить, какая систематическая погрешность в результатах одной из выборок не будут отмечены при сопоставлении на объединение двух выборок: x 1i = 2,39 2,33 2,32 2,39 2,32 x 2i = 2,36 2,40 2,37 2,39 2,30 Решение: Вычислим средние значения и стандартные от- отклонение для обеих выборок: s x1 =0,075 s x2 =0,075. Понятно, что тест на однородность выборки прходится. Средневзвешенное стандартное отклонение останется таким же s 12 = s x1 = s x2 =0,075. Разница между средними значениями двух выборок по уравнению (11) должна удовлетворять условию
Δ x12 = Значит разница Δ x адд = Δ x граничн - Δ x12 = 0,095 может быть добавлена ко всем измеренных значений первой выборки. Допустимая отрицательная систематическая погрешность для первой выборки Δ x адд = Δ x граничн + Δ x 12=0.123. Для второй виборки допустимые систематические погрешности меняют знак. Таким образом ко всем измеримых значений первой
Таблица 4 Значение критерия Фишера, F (f 1, f 2, P=0,95).
При обработке результатов химического анализа систематические погрешности должны быть выявлены и устранены или, по крайней мере, оценены. Один из способов выявления систематической погрешности (проверка правильности) - варьирование величины пробы. Удваивая (способ удвоения) или увеличивая размер пробы в кратное число раз, можно обнаружить по изменению найденного содержания компонента, определяющие (см. Рис. 1.3) постоянную систематическую погрешность. Существует также способ «введено-найдено», когда к пробе анализируемой добавляется точно известно количество компонента, который определяют. Компонент должен быть добавлен в той же форме, в которой он находится в рассматриваемом объекте и проведен через все стадии анализа. При этом компонент может быть введен в матрицу образца, не содержит компонента, который определяют, или добавлен к образца, содержащего точно установленное количество компонента. Если на последней стадии анализа введена количество компонента определяется с достаточной точностью, то результат анализа считается правильным. Еще одним способом проверки правильности является сравнение результата анализа с результатом, полученным другим независимым методом. При этом химик должен быть уверен в том, что выбранный для сравнения метод (методика) дает правильный результат и действительно независимым, то есть в основу определения компонента положены различные принципы. Например, при проверке правильности определения компонента спектрофотометрическим методом желаемое для сравнения использовать хроматографический, полярографический или потенциометрический метод, но не спектрофотометрический с применением другого реагента. Общепринятый метод оценки правильности - анализ стандартного образца. Это самый надежный способ выявления систематической погрешности. Стандартные образцы изготавливают из материала, состав и свойства которого надежно установлены и официально заверены. Обычно стандартные образцы (на один или более компонентов) анализируют различными методами в нескольких лабораториях, поэтому содержание компонентов, указанный в свидетельстве о составе образца, можно принимать как истинное значение. Непременное условие применения стандартного образца в химическом анализе - максимальная близость соединения свойств стандартного образца и пробы. При использовании стандартного образца для оценки правильности метода или методики проводят многократный химический анализ образца и сравнивают найден содержание с действительным (паспортным) содержанием определяемого компонента.
Оценка правильности метода и методики должна проводиться для нескольких различных содержаний определяемого компонента, то есть с использованием двух или нескольких стандартных образцов. Стандартные образцы используют не только для проверки правильности конечного результата определения компонента, но и на отдельных стадиях химического анализа с целью выявления систематических погрешностей. Сейчас известны государственные стандартные образцы (образцы 1-го разряда) для металлов, сплавов, продуктов и полупродуктов химической промышленности, лекарственных препаратов и т.д. Особенно сложное изготовление стандартных образцов сложных (многокомпонентных, многофазных, неустойчивых во времени) веществ: руд, горных пород, пищевых продуктов, биомасс, объектов окружающей среды. В этих случаях стандартные образцы изготавливают на основе реальных объектов, проводя многократные, сложные химические анализы усилиями различных учреждений, отраслей и даже стран (создание международных стандартных образцов). Для решения ряда проблем, в том числе и для проверки правильности, применяют стандартные образцы 2-го разряда, созданные в отдельных отраслях народного хозяйства, научных и производственных организациях, отдельных лабораториях. Химики-аналитики иногда используют для проверки правильности составлены или синтезированные смеси компонентов, надежно проанализированы химические вещества.
ГРАВИМЕТРИЧЕСКИЙ АНАЛИЗ
Весы и принцип взвешивания Массу вещества m измеряют, взвешивая вещество. Вес Р является пропорциональным массе P = mg, где g - ускорение Взвешивая, силу притяжения сравнивают с известной по величине силой, созданной пружиной, пневматического, гидра-вличним или електродинамичним устройством. Наиболее расп-ространенным является «классический» метод: силу притяжения уравновешивают грузом известной массы на рычаги.
где l1 = l2 тогда m x = ms, M x, M s - моменты силы тяжести, l 1, l 2 длины плеч коромысла, m x, m s массы объекта и гирь - известного груза сравнения. Показания средств измерения веса, Которые применяются по этому принципу, не зависят от ускорения силы тяжести. Весы классифицируют, выделяя: стандартные- Iа, I, II, III, IV розрядов; лабораторные общего назначения 1, 2, 3, 4 классов. Согласно классифицируют и гири.
Конструкция аналитических весов В современные аналитические весы вмонтирован интер-фейсы, Которые соединяют устройства.В этих весах полностью автоматическая внутренняя градуировка с учетом температуры, устройства для тарирования во всем диапазоне взвешивания, наделенные унифицированными набором средств автоматизации. На рис. 1 показано аналитические весы фирмы Sartorius.
Рис. 1.1
Одной из наиболее распространенных в нашей стране моделей аналитических весов является ВЛР-200г, схему которых представлена на рис. 2. В них встроена гиря на неполную навеску и шкалу. Основные узлы весов: основа (1), коромысло (10) со стрелкой, сережки (8) с подвесками (3), успокоители колебаний (5) коромысла, гиревой механизм (15), изолир (6), оптическое устройство с экраном (17) для отсчета, делительное устройство (16), кожух, трансформатор. На основе закреплена стойка (13), нижняя часть которой закрыта кожухом (4). Ручкой, расположенной под основанием в центре, настраивают четкость изображения шкалы.Двумя из трех ножек (18), которые вкручены в
Рис. 1.2 основу, устанавливают ее в горизонтальное положение. На коромысле закреплено: опорную призму (12), седла с грузоприемными призмами (7). Положения равновесия коромысла регулируют винты с тарированными гайками (9), которые вкручены слева и справа в коромысло. Центр тяжести подвижной части регулируют винтом (11) с соответствующими гайками. Воздушные успокоители колебаний коромысла - это 2 пары корпусов, верхних (стаканов) и нижних, закрепленных на плате весов. Гиревой механизм накладывает вмонтированные гири (14) на планку правой серьги или снимает их. На боковую стенку кожуха весов вынесено ручку управления механизмом. Ее поворотам соответствуют цифры в окне кожуха, указывающие массу (в сотнях миллиграмм - по лимбу гиревому механизму. На оптическую шкалу нанесены отметки:101 оцифрованная (от 0 до 100), а вдоль них − по 12 запасных. Они дают отсчет в десятках и единицах миллиграммов. Отсчет в сотых долях миллиграмма по диску дилительного устройства. Рис. 1.3. Суммарный отсчет – 0,54060 г. Чтобы снимать показания шкалы, на экране есть отметка - два параллельных штриха. Ручка механизма регулирования нулевой позиции шкалы вынесена на боковую стенку кожуха. Весы включают поворотом любой ручки в верхнее положение. Возвращая их в нижнее положение, выключаем весы: изолируем коромысло и серьги; а пружины арретира касаются чаш. В механизм изолира входят: валик с эксцентриками, штанга изолиру, рычаги с подхватами, арретира (2), и две ручки, которые вынесены на боковые стенки основания весов. Технические характеристики весов ВЛР-200 Наибольший предел взвешивания – 200 г Цена делений шкалы − 1 мг Дискретность отсчета – 0,05 мг Границы погрешностей взвешивания по шкале − ± 0,15 мг Размах и непостоянство показаний нагруженных весов − <0,15 мг Погрешность, обусловленная неравноплечностью − <1 мг Предельная погрешность при навеске: до 25 г ± 0,25 мг
от 25 до 100 г ± 0,5 мг от 100 до 200 г ± 0,75 мг Время успокоения колебаний < 25 cек
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.153.251 (0.014 с.) |


 .
.

 .
.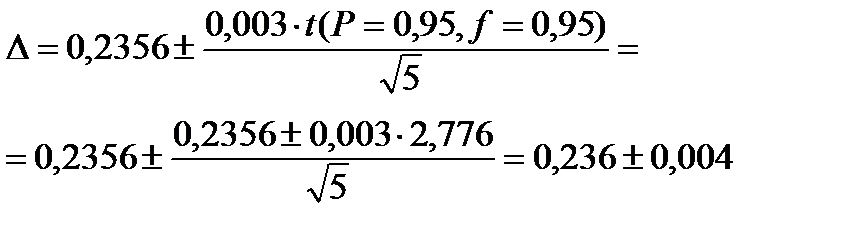
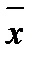 1,
1, 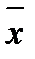 2 и дисперсии,
2 и дисперсии, 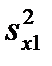 ,
,  .
.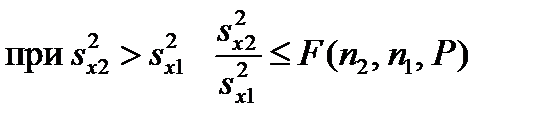
 (9)
(9)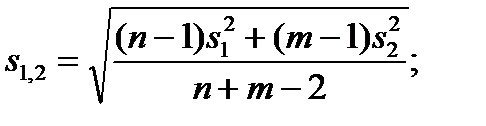 (10)
(10) . (11)
. (11) =2,349
=2,349 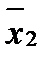 =2,363
=2,363 ,
,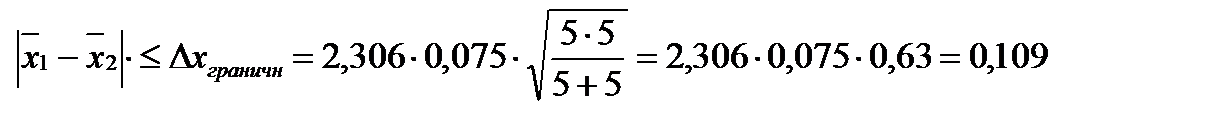 Разница двух средних значений:
Разница двух средних значений: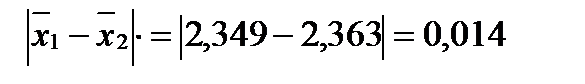 .
.





