
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод материального баланса при расчетах равновесного состава растворовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При растворении в воде соединений - сильных электролитов (какие полностью распадаются на ионы) - за условия ионы, что образуется в растворе не вступают в другие реакции, равновесный состав частично можно описать на основе уравнений материального баланса. Пример 1. Растворением в воде соли MgCl2 приготовили раствор с концентрацией 0,25 моль/л. Какой равновесный состав раствора? Решение: При растворении в воде MgCl2 каждая условная молекула порождает 1 ион Mg2+ и два иона Cl-. Значит [Mg2+] = 0,25 моль/л, a [Cl-] = 0,50 моль/л. Поскольку при участии воды в таком-то H2O D H++OH- KW = [H+]·[OH] = 10-14, (a) материальный баланс по протонам (или по гідросид-ионам) имеет вид: t(H+) = [H+] – [OH] = 0 (b) из уравнения (а) выражаемый равновесную концентрацию иона гидроксида [OH] = kw/[H+] и подставим в уравнение (b): [H+] – kw / [H+] = 0 [H+]2 = kw =10-14 [H+] =10-7 моль/л, И в результате [OH] = 10-14/10-7=10-7
Ответ: [Mg2+] = 0,25; [Cl-] = 0,50 моль/л; [H+] = = [OH-] =10-7 моль/л. Если ионы, которые образовались при растворении соли участвуют в других реакциях с образованием новой частицы, каждая такая реакция характеризуется отдельной константой равновесия, а значит формируется независимое уравнение константы равновесия закона действующих масс. В итоге число уравнений равняется числу новых неизвестных равновесных концентраций ионов и молекул. Из указанного в этом абзаце выплывает вывод о том, что объединение уравнений материального баланса и уравнений констант ЗДМ для равновесной системы раствора с известными общими концентрациями классов компонентов обеспечивает расчеты равновесного состава. Пример 2. растворения в воде соли HCOOH Ag приготовили раствор с концентрацией 0,1 моль / л. Который равновесный состав раствора? (HCOO- - анион муравьиной кислоты, формиат-ион). Решение: В растворе присутствующие такие частицы: Ag+, HCOO-, H+, OH-, AgOH, Ag(OH)2-, HCOOH. Комментарии: Первые две частицы образовались при растворении в воде муравьинокислого серебра. Следующие две - при дисоциации воды. Гидроксокомплексы серебра образовались при взаимодействии с водой ионов Ag+. 1) Ag+ + H2O D AgOH + H+ βОH1KW =102·10-14 = 10-12
Константа ЗДМ для реакции (1) состоит с констант двух реакций (b), (c):
H2ODH++OH- KW = 10-14 = Ag+ + OH- D AgOH βОH1 = 102 = Ag+ + H2O D AgOH + H+ βОH1KW = 102·10-14. Аналогично константа ЗДМ (d) для реакции (2) состоит с констант двух реакций (e),(g): 2) Аg+ + 2H2OD Ag(OH)2- +2H+ βОH2KW2 = 104·(10-14)2 =10-24 βОH2KW2 =
-------------------------------------------------------- 2H2O + Аg+DAg(OH)2- +2H+ βОH2KW2 = 10-24. Последняя частица - диссоциированных формула муравьиной кислоты, образуется в результате взаимодействия с протонами воды формиат-иона: HCOO- + Н+ D HCOOН βH1 = 103,745 = Обращаем внимание! Чтобы назвать все частицы, образующиеся в растворе, необходимо проконтролировать наличие констант ЗДМ Ионы и молекулы, присутствующие в растворе образуют классы частиц - группы ионов и молекул, в состав которых входит один и тот же атом, или одна и та же группа атомов. В нашей задаче образовалось три класса частиц:
1) класс ионов серебра: Ag+, AgOH, Ag(OH)2-; 2) класс формиат ионов: HCOO-, HCOOH; 3) класс ионов водорода: H+, OH-, AgOH, Ag(OH)2-, HCOOH. Для каждого из трех классов записывают уравнения t(Ag+) = [Ag+]+[AgOH]+[Ag(OH)2-] = c(HCOOAg) = 0,1 (k) t(HCOO -) = [HCOO-]+[ HCOOH] = c(HCOOAg) = 0,1 (1) t(H+) = [H+]+[ HCOOH] – [OH] – [AgOH] –2[Ag(OH)2-] = 0 (m) Из уравнений (a), (d), (h) выражают соответственно [AgOH], [Ag(OH)2-], [HCOOH] подставляют их в уравнение (k) и (l) и получают соответственно выражения для [Ag+]и [HCOO-]]
После подстановки уравнений (n) и (o) в уравнение ЗДМ (a), (d). (H) выражают [HCOOH], [AgOH], [Ag(OH)2-] и подставляют в уравнение материального баланса по водороду (m), дополнительно заме-нюють [OH] на KW/[H+]. В результате получают уравнение, в котором только одна неизвестная. Это - [H+]·[H+]+
Для формирования системы уравнений для расчета равновесного состава раствора методом материального баланса удобно воспользоваться матрицей стехиометрических коэффициентов: 1) Выделяют независимые компоненты многокомпонентной системы - компоненты, которые присутствуют в растворе и не образуются при взаимодействии с другими ионами (молекулами). При взаимодействии с другими частицами в растворе каждый из независимых компонен-тов образует отдельный класс. Для примера 2 - это Ag+, HCOO- и H+. 2) Строят матрицу стехиометрических коэффициентов. В 2-4 столбиках матрицы указывают стехиометрические коэффициент в реакциях образования продуктов с участием независимых компонентов. 5 столбик - это продукты реакции, среди которых в верхней части указывают и независимые компоненты. Это значит, что среди продуктов будут все ионы и молекулы, присутствующие в растворе. В 6 столбце указывают логарифмы констант равновесия образования каждого из продуктов. Для независимых компонентов константа равновесия тождественна единицы. Равновесная концентрация каждого из продуктов равна произведению константы равновесия и равновесных концентраций независимых компонентов в степенях соответствующих стехиометрических коэффициентов. Например, (см. 7 строчку):
[Ag(OH)2-] = 10-24[Ag+][H+]-2. Матрица стехиометрических коэффициентов
Уравнение материального баланса для каждого класса (диф. Уравнения (k, l, m)) равны сумме произведений равновесных кон-центраций продуктов (столбик 5) и стехиометрических коэффициентов соответствующего независимого компонента. Подстановка в уравнение матервльного баланса по водороду (m) дает уравнение (p). После возведения в уравнении (p) к общему знаменателю числитель образует уравнение с неизвестным в 5 степени.
Обращаем внимание! После подстановки значений получаем: 103,745·10-1·10210-14·[H+]5 + (103,745–103,745·10-14·0,1) [H+]4 + 10-9.45 [H+]5 +103,745 [H+]4+[H+]3+10 -25,824· [H+]2 – 10-24 = 0. После возведения подобных: [H+]5 + 1013,195[H+]4 +109,45 [H+]3 +10 -16,374·[H+]2 – 10-14,55 = 0. После решения уравнения значение равновесной концентрации [H+] подставляют в уравнение (b), (n), (o) - находят [OH], [Ag_+], [HCOO-]. Исходя из последних по уравнениям (a), (c) зна-ходят концентрации [Ag (OH)], [Ag (OH)2-]. Понятно, что решение такого уравнения высокой степени достаточно громоздкое, оно неудобное для создания компьютерных программ решения, требует алгебраических упрощений. Чтобы не иметь дело с громоздкими уравнениями, надо выделить среди химических равновесий в растворе такое равновесие (такую химическую реакцию), для которой значение константы равновесия с участием превосходящих компонентов (часто они являются независимыми) наибольшая. Если такое равновесие удалось найти, то используют уравнение закона действующих масс для этого равновесия и расчитывают равновесные концентрации участников реакции по схеме М. П. Комарова. Стехиометрия реакции и уровень концентраций реагентов. Если константа ЗДМ достаточно близка к 1, а ее логарифм до 0, вывод, в какую сторону смещен равновесие, не так тривиален. Для реакции (1) размерность концентрационного константы ЗДМ - это (моль/л) a, где a = S a j - сумма стехиометрических коэффициентов при всех реагентах, кроме растворителя, Н2О и реагентов в твердых фазах. Тривиальная оценка справедлива, если a= 0, или концентрация по порядку величины близки к Cr2O72‑ + H2O D 2 HCrO4‑, lg K = ‑1,97 [ I = 1], Если (а) с (Cr2O72‑) = 0,005 моль/л; (b) с (Cr2O72‑) = 5×10‑5 моль/л Хотя константа достаточно мала (К» 0,01), а положительная сумма всех стехиометрических коэффициентов (-1)+2=1, и имела исходная концентрация способствуют смещению равновесия реакции вправо. Оценивая этот эффект, рассчитаем равновесный состав, оснований-ляючы к ЗДМ выражения [А j ]» с * j = сj + х × a j. Два варианта:
Подставляя формулы из строки [] в ЗДМ, имеем уравнение (2 x)2 / (0,005 – x) = 10‑1,97, 4 x 2 + 10‑1,97 x – 0,005×10‑1,97 = 0, С положителльным корнем x = 2,56×10‑3 моль/л, [Cr2O72‑] = 0,005 – x = 2,44×10‑3 моль/л, [HCrO4‑] = 2 x = 5,12×10‑3 моль/л.
Доля выходного Cr2O72‑, что осталась при переходе к равновесию, это x / 0,005 = 0,512, або 51,2 %. Аналогичные расчеты для варианта (b) дают x = 4,91×10‑5 моль/л, [Cr2O72‑] = 5×10‑5 – x = 9×10‑7 моль/л, [HCrO4‑] = 2 x = 9,82×10‑5 моль/л, x / 5×10‑5 = 0,982, або 98,2 %. Рассмотрим еще, какая реакция отвечает за растворения Ag2S(s) в азотной кислоте, c (HNO3) = 3 моль/л. Кислота HNO3 практически сильна - полностью ионизированной. Итак c (HNO3) = 3 моль/л фактически означает c (H+) = c (NO3‑) = 3 моль/л.. Сульфид растворяется или через кислотно-основные свойства аниона S2‑, связывается с Н+ или через окисление сульфидной серы до элементной действия окислителя, иона NO3‑. Рассмотрим эти возможности. Первой отвечает линейная комбинация реакцій
Для очень малой К нечего надеяться на заметное смещение равновесия вправо. Второй возможности соответствует линейная комбинация
Эта константа значительно больше, чем предыдущая, и различные стехиометрические коэффициенты призывают к более подробному исследованию. Составим схему Комаря,
Решая соответствующее уравнение ЗДМ, (6 x)6 / {(3 – 2 x)2 (3 – 8 x)8} = 10‑5,8, имеем x = 0,080 моль/л, [NO3‑] = 3 – 2 x = 2,840 моль/л, [H+] = = 3 – 8 x = 2,360 моль/л, [Ag+] = 6 x = 0,480 моль/л, S (Ag2S(s)) = 3 x = 0,24 моль/л, а это не такая уж маленькая величина! В уравнение ЗДМ не входил р (NO(g)), парциальное давление газа, потому что в исследованной модели процесса мы предполагали, что р (NO(g)) = 1 атм, а избыток газообразного продукта на этой величиной выходит из раствора - раствор является насыщенным относительно продукта NO(g)По справочным данным, растворимость NO(g) в воде равна 33,3×10‑3 моль/л при 0 оС та 1,05×10‑3 моль/л при 60 оС. По уравнению реакции, концентрация продукта NO равна 2 x = = 0,160 моль/л, а это существенно превышает растворимость, и модель подтверждено. В практической работе систему подогревают. Это меняет константы равновесия (направление определяется знаком D H реакций), ускоряет превращение, уменьшает растворимость NO(g) и способствует изъятию его из системы. С нашей оценки следует возможность процесса и в обычных условиях. Ниже приведены несколько примеров решения задач на расчеты равновесного состава растворов.
Примеры вычислений равновесных концентраций расстворов по схеме Комаря М. П. Рассмотрим пример 2, который приведен в разделе «Метод материального баланса» Решение. При растворении соли HCOOAg в воде - в расстворе будут такие преобладающие компоненты: Ag+, HCOO-, H2O Запишем все равновесия в растворе и приведем значения констант ЗДМ: H2O D H++OH- lg KW = -14 Ag+ + H2O D AgOH + H+ lg βОH1KW = -12 Аg++2H2O DAg(OH)2- +2H+ lg βОH2KW2 = -24 HCOO- + H2O D HCOOН +OH- lg βH1KW = -10.255 Среди приведенных реакций для последней - реакции гидролиза формиат-ионов - константа ЗДМ(10-10,255)наибольшая. Рассмотрим последнюю равновесие подробнее. В первой строчке после уравнения реакции указывают исходные данные, во второй - координату реакции, а в третий - равновесный состав (x - равновесная концентрация продуктов реакции) HCOO- + H2O D HCOOН +OH- 1) С0 0,1 - - 2) ΔС - x x x 3) [ ] 0,1- x x x Подставляют равновесные концентрации с 3-й строки в уравнение ЗДМ: 10-10,255 = Решая квадратное уравнение, находят равновесные концентрации [HCOOН] та [OH-]. х 2 + 10-10,255 х – 10-11,255 = 0. Если принять условие x <<0,1, то х 2 = 10-11,255 і х = 10-5,647моль/л (Условие оправдывается, значит решение правильное). Таким образом [HCOOН]= [OH-]=10-5,65 моль/л; [HCOO-] = 0,1–10-5,65 ≈ 0,1 моль/л; [Ag+] ≈ С(Ag+) = 0,1 моль/л; [H+] = KW/[OH-] =10-14/10-5,65 = 10-8,35моль/л, pH = 8,35; [AgOH] = [Ag+]βОH1KW/[H+] = 0,1 10-12 /10-8,35 = 10-4,65 моль/л. Відповідь: [HCOOН]= [OH-] = 10-5,65 моль/л, pH = 8,35 [HCOO-]= = 0,1 моль/л; [Ag+] = 0,1 моль/л, [H+] =10-8,35 моль/л, pH = 8,35, [AgOH] = 10-4,65 моль. Рассмотрим еще несколько достаточно простых примеров с использованием концентрированных констант. Пример 3. Рассчитать рН и равновесный состав раствора уксусной кислоты с концентрацией 0,1 моль / л. Решение. В растворе будут такие преобладающие компоненты: СН3COOН (уксусная кислота), H2O. Запишем равновесия в растворе и приведем значение Термодинамических констант ЗДМ:
H2O D H++OH- lg KW = -14 СН3COOН D СН3COO- + H+ lgKa = -lg βH1 = -4,76 Понятно, что константа второй равновесия значительно выше. Поэтому подробно рассматриваем равновесие диссоциации уксусной кислоты. СН3COOН D СН3COO- + H+ 1) С0 0,1 - - 2) ΔС - x x x 3) [ ] 0,1- x x x После подстановки равновесных концентраций с 3-й строки в уравнение ЗДМ: Ка1 = Если принять условие x x <<0,1, то х 2 = 10-5,76 і Таким образом, [СН3COO-] = [H+] = 10-2,88 моль/л; pH=2,88. [OH-] = KW/[H+] =10-14/10-2,88 = 10-11,12 моль/л, [СН3COOH]=0,1- 10-2,88 = 0,09868 моль/л. Вычислим значение концентрационных констант. Ионная сила раствора: I = 1/2([H+]·12 + [СН3COO-]·12) = 10-2,88. Ионы ОН- не вносят значимого вклада в ионную силу. Коэффициент активности однозарядный иона
lg K c = lg K −
В результате получаем: [СН3COO-] = [H+] = 10-2,9 моль/л; pH=2,9. [OH-] = KW/[H+] = 0-14/10-2,9 = 10-11,1 моль/л, [СН3COOH]=0,1– 10-2,9 = 0,09874 моль/л. Ответ: [СН3COO-] = [H+] = 10-2,9 моль/л; pH = 2,9. [OH-]=10-11,12 моль/л, [СН3COOH] = 0,09874 моль/л.
Примечание. Как видно при сопоставлении, равновесные концентрации, рассчитанные с использованием термодинамического и концен- трацийнои константы, отличаются мало. Пример 4. Рассчитать рН и равновесный состав розчну ги-дроксиду бария с концентрацией 0,01 моль / л. Решение: в растворе будут такие преобладающие компоненты: [Ba2+], [OH-], H2O. Запишем равновесия в растворе и приведем значения констант ЗДМ: H2O D H++OH- lg KW = -14 Ba2+ + OH- D Ba(OH)+ lg βOH1 = 0,5 Оценим ионную силу раствора и концентрационные константы. I = 1/2([Ba2+]·22 + [OH-]·12 =1/2(0,01·4 + 0,02·12 ) = 0,03. Вычислим значение коэффициента активности однозарядный иона
Концентрационный константа первой равновесия: lg Kwc = lg Kw –lg gH+ – lg gOH- = -14–2·(-0,0693)=-13,86 Концентрационный константа второй равновесия:
Рассматриваем подробно последнюю равновесие Ba2+ + OH- D Ba(OH)+ lg βOH1 = 0,916 1) С0 0,01 0,02 - 2) ΔС - x - x x 3) [ ] 0,01- x 0,02- x x После подстановки равновесных концентраций в ЗДМ 100,916 = 2·10-4 − 2·10-2 x − 1·10-2x + x 2 = 0,1213 x x 2 − 0,1513 x + 2·10-4 = 0 x1 = 0,1499, x2 = 1,28·10-3 В результате имеем: [Ba2+] = 0,01−1.28·10-3 = 8,72·10-3 моль/л; [OH-] = 0,002−1.28·10-3 = 1,87·10-2 моль/л; [H+] = KW/ [OH-]= 10-13,86/10-1,728 =10-12,13 моль/л. pH = 2,13. Ответ: [Ba2+] = 8,72·10-3 моль/л; [OH-] = 1,87·10-2 моль/л; [H+] = 10-12,13 моль/л. pH =12,13. Пример 5. Рассчитать равновесный состав и рН насыщенного раствора гидроксида кальция при наличии NaOH с концентрацией 0,1 моль / л. Решение. В насыщенном растворе подтверждается конс- танта «произведение растворимости» (Ks). В исходном растворе (c (NaOH) = 0,1) ионная сила I = 0,1 (проверьте самостоятельно). Коэффициент активности однозарядный иона
Коэффициенты активности ионов-участников равновесия: lggCa2+ = 22·lg g1± = 4 ·(-0,1051)=-0,4204; lggOH- = lg g1±= -0,1051. Вычислим значение логарифма концентрационного константы
Ca(OH)2↓ D Ca2+ + 2OH- lg Ks = -4,665 С0 0,1 ΔС - x x x [ ] x 0,1+ x 10-5,19=[ При условии x <<0,1 имеем: x=[ Ca2+]=10-4,665/0,01=10-2,665 моль/л. [OH-] = 0,1+10-2,665 = 0,1022 моль/л. [H+] = KW/ [OH-] = 10-14/10-0,991 = 10-13,009моль/л, pH = 13 [Na+] = 0,1 моль/л. Ответ: [Ca2+] = 0,0696 моль/л; [OH-] = 0,1022 моль/л; [Na+] = 0,1 моль/л, [H+] = 10-13,009моль/л, pH = 13.
Пример 6. Рассчитать рН и равновесный состав раствора гидрокарбоната натрия с концентрацией 0,1 моль / л. Решение. В растворе кислой соли (преобладающие компоненты - Na+, HCO3-, H2O) имеют место следующие равновесия: HCO3- D CO32-+H+ lgKa2=-lg βH1 =-10,33; HCO3- +H2OD H2CO3+OH- lgKw+lg KH2=-14+6,35=-7,65; 2HCO3-D H2CO3 + CO32- lg KH2 -lg KH1=6,35–10,33=-3,98; H2O D H++OH- lg KW=-14. Рассматриваем подробно равновесие 2HCO3-D H2CO3 + CO32- lg KH2 / KH1 = -3,98. Выполним расчеты концентрационного константы. Ионная сила раствора: I = ([HCO3-]12 +[Na+]12 )/2 = 0,1. Вычислим значение коэффициента активности однозарядный иона
Значит lggCO32- =22·lg g1±=4 ·(-0,1051) = -0,4204; lggHCO3-= lg g1±= -0,1051. Вычислить значение логарифма концентрационного константы
продолжаем анализ равновесия 2HCO3-D H2CO3 + CO32- lg KСH2 / KH1 = -3,665; С0 0,1 ΔС -2 x x x [ ] 0,1-2 x x x После подстановки равновесных концентраций в ЗДМ 10-3,665 = 10-1,833 = 0,0147= х = [H2CO3 ] = [CO32-] = 1,43·10-3 моль/л. [HCO3-] = 0,1− 2[CO32-] = 0,0971 моль/л. [H+] = [OH-] = KW/[H+] =10-14/10-8,5=10-5,5моль/л. Ответ: [HCO3-] = 0,0971 моль/л; [H2CO3 ] = [CO32-] = 1,43·10-3 моль/л; [H+] = 10-8,5; рН = 8,5; [OH-] =10-5,5 моль/л.
БУФЕРНЫЕ РАССТВОРЫ Если к раствору характерное свойство сохранять значение любой равновесной концентрации (активности) при его развел-дневные или добавлении к нему других реактивов, то такой раствор называют буферным относительно этого компонента или показателя, который рассчитывается из равновесную концентрацию (активность) компонента. Известны буферные растворы рН (pH = -lg[H+]), pM (pM = -lg[Mμ+]), pe- (pe = -lg[e-] = f ([Ox]/[Red]). Последние из названных поддерживают значение окислительно-восстановительного потенциала который является мерой равновесной концентрации (активности) несвязанных электронов. Биологические системы проявляют буферные свойства относительно рН и ре-. Свойство противодействовать изменениям снаружи w = DC(H+)/DpH = (при (DС"0)) = dC(H+)/dpH. Классическое определение - это концентрация сильной кислоты (или щелочи), добавление которых изменяет рН на ± 1,0. Буферный раствор рН содержит два компонента, что превращаются друг в друга, присоединяя или теряя протон. Для раствора слабой кислоты и ее соли (например, уксусной) исполняется константа диссоциации:
CH3COOH D CH3COO- + H+ Ka = После логарифмирования имеем:pH = pKa +lg Значение водородного показателя такого раствора определяется значением константы диссоциации и соотношением равновесных концентраций кислоты и ее аниона. При введении в раствор слабой кислоты и соли этой же кислоты равновесные концентрации кислоты и аниона отличаются от введенных на незначительную величину. Если менять соотношение концентраций от 1:100 до 100: 1 можно изменять рН раствора рКа - 2 до рКа + 2 Именно в этом диапазоне (рКа ± 2) на практике готовят буферные растворы рН. Например: следующие значения рКа слабых кислот: рКа(CH3COOH D CH3COO- + H+) = 4,76; рКа(NH4+ D NH3+ H+) = 9,24; рКа1(H3PO4 D H2PO4- + H+) = 2,15; рКа2(H2PO4- D HPO42- + H+) = 7,20; рКа2(HPO42- D PO43- + H+) = 12,35. Вычислим диапазоны рН, в которых можно приготовить соответствующие буферные растворы. Уксусно-ацетатные буферные растворы можно приготовить в диапазоне рН = 4,76 ± 2 = 2,76 – 6,76. Аммонийно-аммиак буферные растворы готовят в диапазоне рН = 9,24 ± 2 = 7,24 – 11,246. А фосфатные буферные растворы можно приготовить в диапазонах рН = pKa1 ± 2 = 0,15 – 4,15; рН = pKa2 ± 2 = 5,2 – 9,2; рН = pKa3 ± 2 = 10,35 – 14. Следует обратить внимание на то, что в сильнокислых (рН≤2) и сильнощелочную (рН≥ 12) средах на практике растворы слабых кислот не используют. При необходимости такие среды создают растворами сильных кислот и сильных оснований (щелочей).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.016 с.) |


 (b)
(b) (c)
(c) . (d)
. (d) . (h)
. (h) , (n)
, (n) . (o)
. (o) –
–  –
–  –2
–2  = 0. (p)
= 0. (p)

 =
= 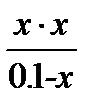 .
. =
=  =
=  = -0,0173;
= -0,0173; lg (
lg ( ) = -4,76 + 1·(-0,0173) + 1·(-0,0173)=-4,79;
) = -4,76 + 1·(-0,0173) + 1·(-0,0173)=-4,79; = 10-4,79; Якщо x<< 0,1 то x 2 = 10-5,79, а x = 10-2,9.
= 10-4,79; Якщо x<< 0,1 то x 2 = 10-5,79, а x = 10-2,9. =
=  = 0,0045 – – 0,0738 = -0,0693; g1±=0,852.
= 0,0045 – – 0,0738 = -0,0693; g1±=0,852. ; lggBa2+=22·lgg1±=-0,2772;
; lggBa2+=22·lgg1±=-0,2772; .
.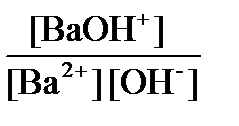 =
= 
 =
=  = -0,1051.
= -0,1051. = ‑5,19+0,420+0,105=-4,665;
= ‑5,19+0,420+0,105=-4,665;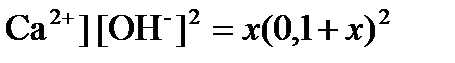 .
. =-0,1051.
=-0,1051. =-3,98+0,420−0,105=-3,665.
=-3,98+0,420−0,105=-3,665. =
=  .
. , 0,00147=1,0294 x.
, 0,00147=1,0294 x. 10-10,33 = 10-8,5 рН=8,5.
10-10,33 = 10-8,5 рН=8,5. .
. .
.


