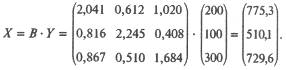Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципиальная схема межотраслевого балансаСодержание книги
Поиск на нашем сайте
Рассмотрим схему МОБ в разрезе его крупных составных частей. Выделяются четыре части, имеющие различное экономическое содержание, которые называются квадрантами баланса и на схеме обозначены римскими цифрами. Первый квадрант МОБ – это прямоугольная таблица межотраслевых материальных связей. Показатели таблицы представляют собой величины прямых межотраслевых потоков продукции и обозначаются как хij, где i и j – соответственно номера производящих и потребляющих отраслей. Таким образом, этот квадрант имеет вид квадратной матрицы п, сумма всех элементов которой равна годовому фонду возмещения затрат средств производства в материальной сфере. Во втором квадранте представлена конечная продукция всех отраслей, выходящая из сферы производства на потребление и накопление. В таблице этот раздел дан укрупненно – в виде одного столбца величин yi, но в развернутой схеме МОБ конечный продукт каждой отрасли дается дифференцированно по направлениям использования: на личное и общественное потребление, на накопление, экспорт и т.д. Следовательно, второй квадрант характеризует отраслевую материальную структуру национального дохода. Третий квадрант МОБ также характеризует национальный доход, но со стороны его стоимостного состава, как сумму чистой продукции и амортизации; чистая продукция понимается при этом как сумма оплаты труда и чистого дохода отраслей. Сумму амортизации Cj и чистой продукции (Vj + mj) j -й отрасли будем называть условно чистой продукцией и обозначать в дальнейшем как Zj. Четвертый квадрант, который находится на пересечении столбцов второго квадранта и строк третьего квадранта, отражает конечное формирование и использование национального дохода. Таким образом, общий итог этого квадранта, так же как второго и третьего, должен быть равен созданному за год национальному доходу.
Валовая продукция отраслей не входит в рассмотренные выше четыре квадранта, а представлена в виде столбца справа от второго квадранта и в виде строки ниже третьего квадранта. Строка и столбец валовой продукции замыкают схему МОБ и играют важную роль как для проверки самого баланса, так и для разработки экономико-математической модели МОБ. Если обозначить валовую продукцию некоторой отрасли буквой с индексом, равным номеру данной отрасли, то можно записать два соотношения, отражающих сущность МОБ и являющихся основой его экономико-математической модели. Во-первых, рассматривая схему баланса по столбцам, можно сделать вывод, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли:
Соотношения (25.1) задают систему п уравнений, отражающих стоимостной состав продукции всех отраслей материальной сферы. Во-вторых, если рассматривать схему МОБ по строкам для каждой производящей отрасли, то можно увидеть, что валовая продукция той или иной отрасли равна сумме материальных затрат отраслей, потребляющих ее продукцию, и конечной продукции данной отрасли:
Формула (25.2) описывает систему из и уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования. Просуммируем по всем отраслям уравнения (25.1), в результате получим:
Аналогичное суммирование уравнений (25.2) дает следующий результат:
Левые части обоих равенств равны между собой, так как представляют собой весь валовой общественный продукт. Первые слагаемые правых частей этих равенств также равны между собой, их величина равна итогу первого квадранта. Следовательно, должно соблюдаться соотношение:
Левая часть уравнения (25.3) есть сумма третьего квадранта, а правая – итог второго квадранта. В целом же это уравнение показывает, что в МОБ соблюдается важнейший принцип единства материального и стоимостного состава национального дохода. Экономико-математическая модель МОБ. Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица является также основой экономико-математической модели МОБ. Предполагается, что для производства единицы продукции в j -й отрасли требуется определенное количество затрат промежуточной продукции i -й отрасли, равное аij. Оно не зависит от объема производства в j -й отрасли и является довольно стабильной величиной во времени. Величины aij называются коэффициентами прямых материальных затрат и рассчитываются так:
Таким образом, имеет место определение: коэффициент прямых материальных затрат аij показывает, какое количество продукции i -й отрасли необходимо для производства единицы продукции j -й отрасли (с учетом только прямых затрат). Используя формулу (25.4), систему уравнений баланса (25.2) можно переписать в следующем виде:
Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А = (aij), а также вектор-столбец валовой продукции X и вектор-столбец конечной продукции Y:
то система уравнений (25.5) в матричной форме примет такой вид: X = AX + Y. (25.6)
Система уравнений (25.5), или она же в матричной форме (25.6), называется экономико-математической моделью межотраслевого баланса (моделью В. Леонтьева, моделью «затраты -выпуск»). С ее помощью можно выполнять три варианта расчетов. 1. Задав в модели величины валовой продукции каждой отрасли (Xi), можно определить объем конечной продукции каждой отрасли (Yi):
Y = (E - A) · X. (25.7)
2. Задав величины конечной продукции всех отраслей (Yi), можно определить величины валовой продукции каждой отрасли (Xi): X = (E – A) -1 · Y. (25.8)
3. Задав для ряда отраслей величины валовой продукции, а для всех остальных отраслей объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. В этом варианте расчета удобнее пользоваться не матричной формой модели (25.6), а системой линейных уравнений (25.5). В формулах (25.7) и (25.8) Е обозначает единичную матрицу n -го порядка, а (Е – A) -1 обозначает матрицу, обратную матрице (Е – А). Если определитель матрицы (Е – А) не равен нулю, т.е. эта матрица невырожденная, то обратная ей матрица существует. Обозначим последнюю так: В = (Е - А) -1
Тогда систему уравнений в матричной форме (25.8) можно записать в виде: X = BY. (25.8)
Элементы матрицы В будем обозначать через bij, тогда из матричного уравнения (25.8') для любой i -й отрасли можно получить следующее соотношение:
Из соотношений (25.9) следует, что валовая продукция выступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты bij, которые показывают, сколько всего нужно произвести продукции i -й отрасли для выпуска в сферу конечного использования единицы продукции j -й отрасли. В отличие от коэффициентов прямых затрат аij коэффициенты bij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства. Более детально этот вопрос рассматривается в следующем разделе.
Дадим определение коэффициента полных затрат: коэффициент полных материальных затрат bij показывает, какое количество продукции i -й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j -й отрасли. Коэффициентами полных материальных затрат можно пользоваться, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей:
где ∆Хij, и ∆ Yj – изменения (приросты) величин валовой и конечной продукции соответственно. Коэффициенты прямых и полных материальных затрат, связь между ними, методы расчета. Переходя к анализу модели МОБ, необходимо прежде всего рассмотреть основные свойства матрицы коэффициентов прямых материальных затрат А. Коэффициенты прямых затрат по определению являются неотрицательными, следовательно, матрица А в целом может быть названа неотрицательной: А ≥ 0. Так как процесс воспроизводства нельзя осуществлять, если для собственного воспроизводства в отрасли затрачивается большее количество продукта, чем создается, то очевидно, что диагональные элементы матрицы А меньше единицы: аii < 1. Система уравнений МОБ является отражением реальных экономических процессов, в которых содержательный смысл могут иметь лишь неотрицательные значения валовых выпусков, поэтому вектор валовой продукции состоит из неотрицательных компонентов. Экономическая система обеспечивает положительный конечный выпуск по всем отраслям, если матрица коэффициентов прямых материальных затрат удовлетворяет условию продуктивности: X > АХ. Это означает существование положительного вектора конечной продукции Y > 0 для модели МОБ (25.6). Рассматривая вычислительные аспекты решения задач на основе модели МОБ, отметим, что основной объем расчетов связан с вычислением матрицы коэффициентов полных материальных затрат В. Если матрица коэффициентов прямых материальных затрат А задана и является продуктивной, то матрицу В можно находить либо по формулам прямого обращения матриц, либо с использованием итерационных методов. Одним из наиболее употребительных методов обращения матриц является метод Жордана. Часто применяется также метод, основанный на применении формулы:
где в числителе стоит так называемая присоединенная матрица, составленная из алгебраических дополнений для элементов транспонированной матрицы (Е – А)', а в знаменателе находится определитель матрицы (Е – A). В свою очередь, алгебраическое дополнение для элемента матрицы с индексами i и j получается путем умножения множителя (–1) i+j на минор, получаемый после вычеркивания из матрицы i -й строки и j -го столбца.
Рассмотрим пример. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:
Необходимо найти коэффициенты полных материальных затрат и вектор валовой продукции, а также заполнить схему межотраслевого материального баланса. 1. Определим матрицу коэффициентов полных материальных затрат, используя формулу (25.11) и методы матричной алгебры:
2. Найдем величины валовой продукции трех отраслей (вектор X), используя формулу (25.8'):
3. Для определения элементов первого квадранта материального межотраслевого баланса в нашей задаче воспользуемся формулой, вытекающей из формулы (25.4): хij = аij · Хj. Из этой формулы следует, что для получения первого столбца первого квадранта нужно элементы первого столбца заданной матрицы А умножить на Х 1 = 775,3, элементы второго столбца А – на Х 2 = 510,1, а третьего столбца – на Х 3= 729,6. Составляющие третьего квадранта (условно чистая продукция) находятся с учетом формулы (25.1) как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта. Четвертый квадрант в нашей задаче состоит из одного показателя и служит, в частности, для контроля правильности расчета: сумма элементов второго квадранта должна в стоимостном материальном балансе совпадать с суммой элементов третьего квадранта. Результаты расчета представлены в табл. 25.2. Таблица 25.2
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.192.109 (0.009 с.) |