Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические данные о расходах на семьюСодержание книги
Поиск на нашем сайте
Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х 1 ). Она выражается линейной функцией следующего вида:
Параметры a 0и а 1можно найти, решив систему нормальных уравнений, которая, в свою очередь, формируется с применением метода наименьших квадратов. Система нормальных уравнений для рассматриваемого случая имеет вид:
где суммирование проводится по всем n группам. Используя данные табл. 25.7, получим систему уравнений:
решением которой являются значения a 0 = 549,68 и а 1= 0,1257. Таким образом, модель имеет вид;
Уравнение (25.73) называется уравнением регрессии, коэффициент а 1называется коэффициентом регрессии. Направление связи между у и х 1определяет знак коэффициента регрессии а 1(в нашем случае данная связь является прямой). Теснота этой связи определяется коэффициентом корреляции:
где Sy есть средняя квадратическая ошибка выборки у в табл. 25.7. Она находится по формуле:
где
где Чем ближе значение коэффициента корреляции к единице, тем теснее корреляционная связь. В нашем примере Sy 2 = 454 070,
Полученное значение Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х 1 ) и размера семей (х 2 ). Множественный (многофакторный) корреляционно-регрессивный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов. В нашем случае эта модель имеет вид:
Параметры модели a 0, а 1 и а 2находятся путем решения системы нормальных уравнений:
Используя данные табл. 25.7, получим систему нормальных уравнений в таком виде:
Решая эту систему (например, методом Гаусса), получим: a 0= 18,63; а 1 = 0,0985; a 2 = 224,6, так что модель (25.75) имеет вид:
Для определения тесноты связи предварительно вычисляются парные коэффициенты корреляции
где черта над символами означает среднюю арифметическую, a Sy и Sx1 – средние квадратические ошибки соответствующих выборок из табл. 27.7. Их можно вычислить следующим образом:
Аналогичный вид имеют формулы для После этого вычисляется коэффициент множественной корреляции:
Данный коэффициент колеблется в пределах от 0 до 1; чем ближе он к единице, тем в большей степени учтены факторы, влияющие на результативный признак. В нашем примере расчеты дают следующие значения коэффициента множественной корреляции: Величина Задача анализа тесноты связи между результативным и одним из факторных признаков при неизменных значениях других факторов решается в многофакторных моделях при помощи частных коэффициентов корреляции. Так, частный коэффициент корреляции между результативным признаком у и факторным признаком х 1при неизменном значении факторного признака х 1рассчитывается по формуле:
где используются парные коэффициенты корреляции, рассчитываемые по формулам, аналогичным (25.77). Аналогичная формула имеет место для частного коэффициента корреляции
Для рассматриваемого примера частные коэффициенты корреляции расходов на питание от душевого дохода и размера семей составляют:
Это означает, что теснота связи между расходами на питание и одним из исследуемых факторов при неизменном значении другого весьма велика. Если частные коэффициенты корреляции возвести в квадрат, то получим частные коэффициенты детерминации, показывающие долю вариации результативного признака под действием одного из факторов при неизменном значении другого фактора. В нашей задаче Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели (25.75) считываются по формулам:
Черта над символом, как и ранее, означает среднюю арифметическую величину. Частные коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным. В рассматриваемом примере а 1= 0,0985; а 2= 224,6;
Это означает, что при увеличении душевого дохода на 1% и неизменном размере семьи расходы на питание увеличатся на 0,456%, а увеличение (условное) на 1% размера семьи при неизменяем душевом доходе приведет к возрастанию расходов на питание на 0,530 %.
Вопросы для повторения
1. Перечислите важнейшие методы экономико-математического моделирования и сферы их оптимального применения в маркетинге. 2. Каков характер применения балансовых моделей в маркетинге? 3. Раскройте сущность модели межотраслевого баланса. 4. Опишите назначение и структуру оптимизационных моделей. Какие задачи маркетинга можно решать с их помощью? 5. Какие важнейшие методы и модели управления товарными запасами используются в маркетинге? 6. Перечислите основные системы регулирования товарных запасов и дайте их краткие характеристики. 7. Дайте определение понятия целевой функции потребления и кривых безразличия. 8. В чем суть построения функций спроса от дохода? 9. Назовите особенности построения структурных и конструктивных моделей спроса. 10. Опишите построение аналитических моделей спроса и потребления на основе корреляционно-регрессивного анализа.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.49.213 (0.01 с.) |


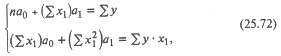
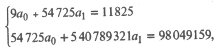


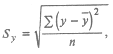
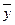 – средняя арифметическая значений у, а
– средняя арифметическая значений у, а 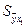 – средняя квадратическая ошибка нашего уравнения (25.73). Последняя определяется следующим образом:
– средняя квадратическая ошибка нашего уравнения (25.73). Последняя определяется следующим образом: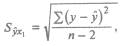
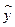 есть соответствующее значение, вычисленное по модели (25.73). В этих формулах, как и ранее, суммирование ведется по всем группам.
есть соответствующее значение, вычисленное по модели (25.73). В этих формулах, как и ранее, суммирование ведется по всем группам.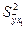 = 63 846, следовательно:
= 63 846, следовательно: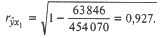
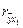 свидетельствует, что связь между расходами на питание и душевым доходом очень тесная. Величина
свидетельствует, что связь между расходами на питание и душевым доходом очень тесная. Величина 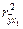 называется коэффициентам детерминации и показывают долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае
называется коэффициентам детерминации и показывают долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае 
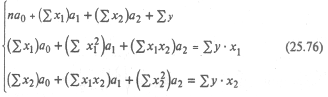
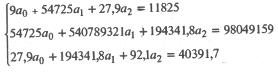
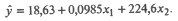
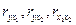 . Например:
. Например:
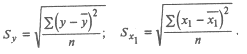
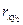 и
и 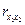 .
.
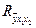 =0,983, что выше значения коэффициента корреляции в случае однофакторной модели. Таким образом, связь расходов на питание с факторами душевого дохода и размера семей является очень высокой.
=0,983, что выше значения коэффициента корреляции в случае однофакторной модели. Таким образом, связь расходов на питание с факторами душевого дохода и размера семей является очень высокой.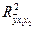 называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. В нашем примере
называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. В нашем примере 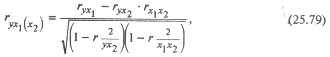
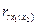 между результативным признаком у и факторным признаком x 2 при неизменном значении факторного признака х 1.
между результативным признаком у и факторным признаком x 2 при неизменном значении факторного признака х 1.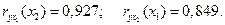
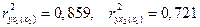 , следовательно, влиянием душевого дохода при неизменном размере семьи объясняется почти 86% изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание.
, следовательно, влиянием душевого дохода при неизменном размере семьи объясняется почти 86% изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание.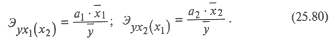
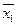 = 6080,6;
= 6080,6; 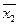 = 3,1, следовательно, по формулам (25.80) получим:
= 3,1, следовательно, по формулам (25.80) получим: