Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики исходных сплавовСодержание книги
Поиск на нашем сайте
Следует определить, какие из исходных сплавов и в каких количествах нужно использовать для получения требуемого сплава, чтобы суммарные затраты на исходные сплавы были минимальными. Сформулируем экономико-математическую модель данной задачи. Обозначим через х 1 х 2, x 3 х 4 х 5искомые количества исходных сплавов. Тогда целевая функция примет вид:
При этом существуют следующие условия:
Сформулированная задача, как и предыдущая, решается методами линейного программирования. Модели оптимального раскроя промышленных материалов. Сущность оптимального раскроя состоит в разработке таких технологически допустимых раскройных планов, при которых из стандартных единиц раскраиваемых ресурсов получается необходимый комплект заготовок требуемого размера, а критерий оптимальности заключается в сведении к минимуму либо общей величины отходов кроя, либо количества раскраиваемых единиц ресурсов. Формулировка задачи оптимального раскроя зависит от формы раскраиваемого материала, который может быть длинномерным, листовым, рулонным и т.д. Сформулируем экономико-математическую модель задачи оптимального раскроя по одному измерению длинномерных материалов (прутков, труб, профильного проката и др.). Примем следующие обозначения: L – длина исходного материала; i – номер (индекс) вида требуемых заготовок, i = 1, 2... т; li – длина заготовки i -го вида; Аi – требуемое число заготовок i -го вида (не менее); j - номер варианта раскроя, j = 1, 2... n; aj – количество заготовок i -го вида при раскрое единицы исходного материала по j -му варианту; сij – длина отхода по j -му варианту. Пусть х 1 - количество единиц исходного материала, раскраиваемых по i -му варианту. Целевая функция по критерию минимума отходов имеет вид:
По критерию минимума раскраиваемых единиц исходного материала уравнение может быть таким:
Это верно при соблюдении следующих условий:
Получилась задача линейного программирования, которую надо пополнить требованием целочисленности величины х j. Заметим, что во многих случаях решения задач с обеими указанными целевыми функциями совпадают. Наиболее трудоемкий этап в процессе построения модели рассматриваемой задачи заключается в определении всех возможных вариантов раскроя. Исходные соотношения для составления вариантов раскроя следующие:
Условие (25.46) означает, что длина отхода для любого варианта раскроя должна быть меньше, длины самой короткой заготовки (это является признаком полноценности варианта). Рассмотрим пример. Снабженческо-сбытовая фирма получает от поставщиков прутки стального проката длиной 600 см. Согласно заявкам потребителей требуются заготовки трех видов в следующих количествах: 150 тыс. шт. длиной 250 см, 140 тыс. шт. длиной 190 см и 48 тыс. шт. длиной 100 см. Сформулируем экономико-математическую модель задачи оптимального раскроя с минимумом отходов. Составим таблицу возможных вариантов раскроя, при этом в первом блоке имеют место варианты раскроя, дающие все три вида заготовок, во втором - дающие заготовки второго и третьего вида, а в третьем – дающие заготовки только третьего вида. Таблица 25.5 Возможные варианты раскроя
Пусть х 1, x 2, x 3, х 4, x 5, х 6, х 7 – количества прутков, раскраиваемых по каждому варианту. Тогда целевая функция имеет вид:
Такое уравнение действительно при следующих условиях:
Задача о коммивояжере. Здесь требуется отыскать наилучший маршрут, с тем чтобы объехать все порученные коммивояжеру пункты и вернуться назад либо в кратчайший срок, либо с наименьшими затратами на проезд. В общем виде эту задачу можно сформулировать следующим образом. Имеется п городов, занумерованных числами от 1 до п. Коммивояжер, выезжая из города 1, должен побывать в каждом городе ровно один раз и вернуться в исходный пункт. Известны расстояния между городами: сij (i, j = Введем переменные:
Требования однократного въезда и выезда из каждого города запишутся в виде:
Однако эти ограничения полностью не описывают допустимые маршруты, так как не исключают возможности разрыва пути, т.е. появления нескольких не связанных между собой подмаршрутов для части городов. Поэтому вводятся дополнительно переменных Ui, которые принимают только целые неотрицательные значения. Тогда можно записать еще (n – 1)2 – (n – 1) ограничений:
Нетрудно показать, что ограничения (25.48) не исключают допустимый маршрут, но исключают возможность существования подмаршрутов. Таким образом, задача о коммивояжере состоит в минимизации:
Это действительно при условиях (25.47), (25.48), где переменные xij, Ui принимают только неотрицательные целые значения. Задача о размещении складов. Она является одной из оптимизационных задач исследования операций и решается обычно методами нелинейного программирования. Надо минимизировать общую сумму транспортных и складских расходов при следующих ограничениях: а) с каждого предприятия должна быть отгружена вся продукция; б) не может быть превышена емкость ни единого склада; в) должны быть удовлетворены заявки всех потребителей. В процессе решения задачи находится оптимальная по минимуму затрат трехчленная комбинация: предприятие – склад – потребитель. При некоторых условиях задача о размещении складов может сводиться к обычной транспортной задаче линейного программирования. Задача о ранце (или о рюкзаке). Так называется задача о наилучшем выборе предметов из общего их количества, т.е. таким образом, чтобы суммарный вес (или габариты) отобранных предметов не превышал (не превышали) заданную величину, а их суммарная полезность или иная общая оценка (количество калорий, общая стоимость и т.д.) была максимальной. Задача о ранце решается как задача целочисленного линейного программирования, методами динамического программирования и другими. В частности, эта задача применяется при планировании оптимальной загрузки самолетов, кораблей, складов и др.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.006 с.) |

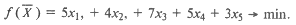
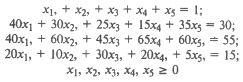


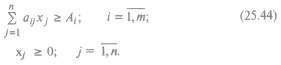
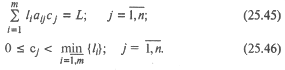
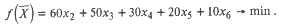
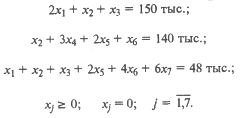
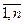 ; i ≠ j). Требуется найти самый короткий маршрут.
; i ≠ j). Требуется найти самый короткий маршрут.