Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Произведением этих величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
J. Корень квадратный из математического ожидания <question> 256Чему равна вероятность того что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения? F. 0,9973++ G. 0,2896 H. 0,1 I. 0,369 J. 0,95
<question>257.Случайная величина X имеет дисперсию D (X) = 0,004. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,2, по неравенству Чебышева является выражение: F. 1-0,004/(0,2)2 +++ G. 0,004/0,2 H. 1-0,004/0,2 I. 1-0,004-(0,2)2 J. (0.2)2/0.004
<question>258.Случайная величина X имеет дисперсию D (X) = 1620. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 200, по неравенству Чебышева является выражение: F. 1-1620/2002 ++ G. 1+1620/2002 H. 1620/2002 I. 2002/1620 J. 1-1620/200 259<question> Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется <variant> бесповторной <variant> репрезентативной <variant> вариативной <variant>равновозможной <variant> повторной+++
260<question>Выборочная совокупность- <variant> совокупность объектов, из которых проводится выборка. <variant> совокупность случайно отобранных объектов+++ <variant> число объектов этой совокупности <variant> отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число) <variant>Cовокупность специально отобранных обьектов
261<question> Генеральная совокупность- <variant> совокупность случайно отобранных объектов. <variant> совокупность объектов, из которых проводится выборка+++ <variant> отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число) <variant> число объектов этой совокупности K. <variant>Cовокупность специально отобранных обьектов
262<question> Объемом совокупности называется <variant> число объектов этой совокупности +++ <variant> совокупность случайно отобранных объектов. <variant> совокупность объектов, из которых проводится выборка. <variant> отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число) <variant>Cовокупность специально отобранных обьектов
263<question> Статистистические распределение <variant> то закон, описывающий область значений случайной величины и вероятности их исхода (появления) <variant> называют таблицу значений признака расположенных в возрастающем порядке, и соответствующих им частот или относительных частот.+++ <variant>мера разброса данной случайной величины, то есть её отклонения от математического ожидания <variant> распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса <variant>все варианты верны
<variant>кривая линия, отрезки которой соединяют точки (xi, ni) <variant> ломаная линия, отрезки которой соединяют точки (xi, ni). <variant>прямая линия, отрезки которой соединяют точки (xi, ni) <variant>косая линия, отрезки которой соединяют точки (xi, ni)
<variant>Все варианты верны
265<question> Бесповторная выборка – <variant> выборка, при которой отобранный объект после проведения обследований возвращается в генеральную совокупность. < variant> выборка, при которой отобранный объект после проведения обследований не возвращается в генеральную совокупность.++++ < variant> выборка, при которой отобранный объект после проведения обследований не возвращается в генеральную совокупность. <variant> Все варианты верны <variant>Все варианты неверны
266<question> Статистические характеристики- <variant>центр,радиус,размер кластера. <variant>Нет правильного ответа <variant>среднее арифметическое,мода,медиана,размах <variant>математичекое ожидание,среднее квадратное отклонение,ассиметрия <variant>плавающая точка,мантисса,механический нуль
267<question> В течении четверти Петя получил следующие отметкипо математике:одну <пятерку>,пять<четверок>,четыре <троек>.На сколько среднее арифметическое оценок Пети отличается от медианы этого ряда чисел? <variant>0.5 <variant>0.7 <variant>0.9 <variant>0.3+++
268<question> Мода ряда чисел <variant> число, редко встречающееся в ряду+++ <variant> это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. < variant> число, наиболее часто встречающееся в ряду <variant> число, наименьше часто встречающееся в ряду 269<question> Медианой ряда <variant> наиболее часто встречающийся вариант ряда <variant> это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две неравные по численности части. <variant> это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.+++ <variant>наименее часто встречающийся вариант ряда <variant> число, редко встречающееся в ряду 270<question> Если выборку отбирают по одному объекту, который обследуют и не возвращают в генеральную совокупность, то выборка называется <variant> репрезентативной <variant> вариативной <variant> бесповторной ++++ <variant> повторной <variant>равновозможной 271<question> Если все объекты генеральной совокупности имеют одинаковую вероятность попасть выборку, то выборка называется <variant>равновозможной <variant> репрезентативной +++ <variant> бесповторной <variant>повторной <variant> вариативной
272<question> В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей? <variant>0.5 <variant>0.25 <variant>0.15 <variant>0.05+++
273<question> При стрельбе из винтовки относительная частота попадания в цель, оказалось равной 0,85.Найти число попаданий,если всего было произведено 120 выстрелов. <variant>120 <variant>1.25 <variant>1.70 <variant>102+++++++ <variant>103
274<question> Из озера выловили 86 рыб, которых пометили и отпустили обратно в озеро.Через неделю произвели повторный отлов,на этот раз поймали 78 рыб,среди которых оказалось 6 помеченных.Сколько приблизительно рыб живет в озере. <variant>58 <variant>1118++++ <variant>1110 <variant>1120 <variant>6536
275<question> Опыт произвели n раз, событие А при этом произошло m раз. Найти частоту появления события А: n=m=100 <variant> 1++ <variant>0,75 <variant> 0,5 <variant>0,1 <variant> 0
276<question> Бросили игральную кость. Какова вероятность, что выпадет четное число очков <variant>0,5++ <variant> <variant> <variant> <variant> 277<question> В ящике 25 шаров, из них 10 белых, 7 голубых, 3 желтых, 5 синих. Найти вероятность того, что наудачу вынутый шар белый. <variant>0,2 <variant>0,4+++ <variant>0,5 <variant> <variant> 278<question> Найти Р (АB), если <variant> <variant> <variant>0,06 <variant>0.1 <variant>
279<question> Найти <variant> 0,5 <variant> 0,8 +++ <variant> 0,2 <variant> 0,6 <variant> 0.16
280<question> События А и В несовместимы. НайтиР(А + B), еслиР(A)= Р(B)= 0,3??? <variant> 0,9 <variant> 0,8 <variant> 0,7 <variant> 0,6+++ <variant> 0,51
281<question> НайтиР (А+B), если Р(A)=Р(B)=0,3 Р(АB)=0,1??? <variant> 0,6 <variant> 0, 9 <variant> 0,5++++ <variant> 0,7 <variant> 0.8
282<question> Опыт произвели n раз. Событие А произошло при этом m раз. Найти частоту появления события А: n = 10, m = 2 <variant> <variant>0,2 ++++++ <variant> 0,5 <variant>0,25 <variant>0,15
283<question> Сумма произведений каждого значения ДСВ на соответствующую вероятность называется. <variant> законом распределения ДСВ <variant> медианой <variant> математическим ожиданием ДСВ <variant> дисперсией случайной величины <variant> средним квадратическим отклонением
284<question> Вероятность безотказной работы одной ячейки доильной установки равна р. Х – число безотказно работающих ячеек доильной установки во время дойки n коров. Найти М (х).??? р = 0,9; n = 10 <variant> 7,2 <variant> 7,8 <variant> 9 <variant> 8,4 <variant> 6
285<question> Вероятность безотказной работы одной ячейки доильной установки равна р. Х – число безотказно работающих ячеек доильной установки во время дойки n коров. Найти Д (х). р = 0,9; n = 10 <variant> 0, 9 <variant> 2,52 <variant> 3, 6 <variant> 1,44 <variant> 0,09
286<question> Задан биномиальный закон распределения ДСВ. Найти М(х).
<variant> 2,4 <variant> 2,8 <variant> 1,2 <variant> 0,8 <variant> 3,2
287<question> Задан биномиальный закон распределения ДСВ. Найти Д(х).
<variant> 0,36 <variant> 0,96 <question> 0,64 <question> 0,84 <variant> 0,24
288<question> Задан биномиальный закон распределения ДСВ. Найти Р (х<2).
<variant> 0,0272 <variant> 0,1792 <variant> 0,2725 <variant>0,3398 <variant> 0,1856
289<question> Найти соответствующую формулу: М(х) =???? <variant> <variant> <variant> <variant> F(b) – F(a) <variant>
290<question> Задан закон распределения ДСВ. Найти М(х). <variant>1,9 <variant> 3,8 <variant>4,2 <variant> 0,7 <variant> 2,1 291<question> Задан закон распределения ДСВ <variant>1 <variant> <variant> <variant> <variant>1-(
292<question> <variant> <variant> 1 <variant> <variant> <variant> 0
293<question> Опыт произвели n раз, событие А при этом произошло m раз. Найти частоту появления события А: n=1000; m=100 <variant>0,1 <variant> 0,75 <variant>1 <variant> 0,5 <variant> 0,01
294<question> Бросили игральную кость. Какова вероятность, что выпадет больше четырех очков <variant> <variant> <variant>0,5 <variant> <variant>
295<question> В ящике 20 стандартных деталей и 7 бракованных. Вытащили три детали. Событие А1 – 1-ая деталь бракованная, А2 – 2-ая деталь бракованная, А3 – 3-ья деталь бракованная. Записать событие: В – все детали стандартные.??? <variant> <variant> 1 <variant> <variant> <variant>
296<question> Кумулята- <variant>кусочно-линейная функция,так как относительные частоты линейно растут на интервале, график накопленных частот <variant> линейная функция,так как относительные частоты линейно растут на интервале, график накопленных частот <variant>Все варианты верны
297<question> Выбрать правильный ответ: <variant>0 <variant>1-P(A) <variant>1-P(͞͞A) <variant> <variant>P(A)+P(͞A)-P(A͞A)
298<question> Гистограмма это <variant> квадратная фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиною h, а высоты n. <variant> ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиною h, а высоты n.++ <variant> ступенчатая фигура, состоящая из труегольников, основаниями которых служат интервалы длиною h, а высоты n. <variant> ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиною n, а высоты h. <variant> треугольная фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиною h, а высоты n.
299<question> В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке равна 0,5. Какова вероятность выигрыша трех предметов? <variant> 0,25 <variant> 0,20 <variant> 0,1 <variant>0,125 <variant> 0,5
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1880; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.135 (0.012 с.) |






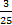


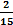 +++
+++
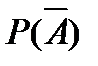 , еслиР(A) = 0,2???
, еслиР(A) = 0,2???
 ????
????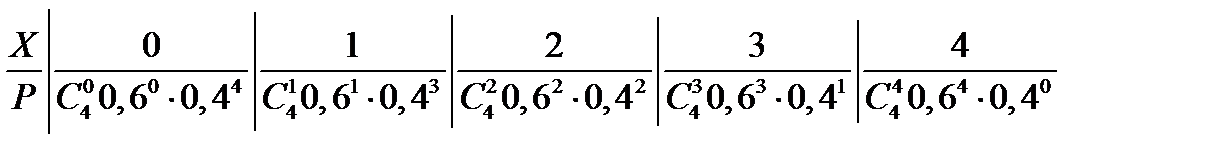 ???
???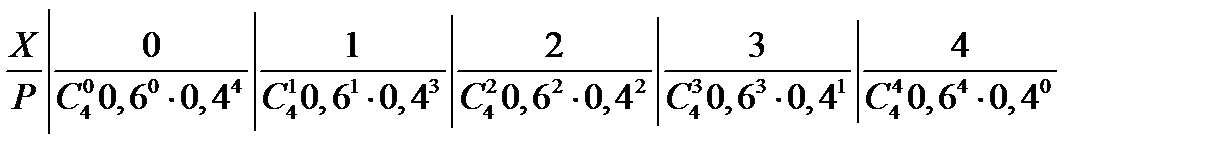 ???
???
 ++++++
++++++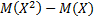
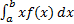
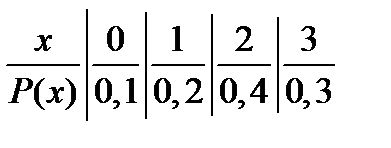 ???
??? . Найти
. Найти 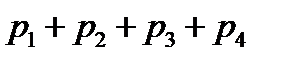 .???
.???
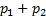
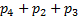
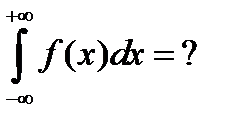
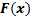

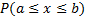

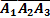 =B
=B 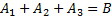
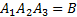
 +
+ 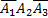 =B
=B