
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод рабочей формулы для экспериментальногоСодержание книги
Поиск на нашем сайте определения момента инерции.
Рис. 4.1 При экспериментальном определении момента инерции используется маятник Обербека, который представляет собой крестовину с четырьмя закрепленными на ней на одинаковых расстояниях от оси одинаковыми грузами. На ось крестовины насажен двухступенчатый шкив, на который намотана нить с подвешенным к ней грузом. При движении груза вниз шкив начинает вращаться. Для вывода рабочей формулы рассмотрим упрощенную схему установки, выделив систему связанных движущихся тел: поступательно движущийся груз и вращающийся шкив (рис. 4.1). Поступательное движение груза описывается уравнением: mg – T = ma (4.1) Вращательный момент шкива создает сила натяжения нити Т 1, которая по третьему закону Ньютона равна силе Т. Этот момент М = ТR. Тогда уравнение вращательного движения шкива: ТR = I ε (4.2) Если отсутствует проскальзывание нити, то тангенциальное ускорение элементов нити, вращающихся вместе со шкивом, равно линейному ускорению груза: а τ = а = ε R (4.3) Решая систему уравнений (4.1), (4.2) и (4.3), получим для момента инерции выражение: Линейное ускорение груза можно вычислить по измеренным высоте падения груза и времени его падения: h = at 2/2. Таким образом, получена рабочая формула для экспериментального определения момента инерции:
Вывод формулы для теоретического вычисления Момента инерции.
Момент инерции является аддитивной величиной, то есть момент инерции системы тел равен сумме моментов инерции всех тел, входящих в систему. Маятник Обербека состоит из шкива (включая ось и втулку крестовины), четырех стержней крестовины и грузов, укрепленных на крестовине. Момент инерции шкива указан на установке. Момент инерции стержня относительно оси, проходящей через его конец, равен m 2 l c2/3, где m 2 − масса стержня без груза, l c − длина стержня крестовины − указаны на установке. Грузы, укрепленные на крестовине, приближенно можно считать за точечные массы. Тогда момент инерции каждого груза равен m 1 l 2, где m 1 − масса одного груза (указана на установке), l − расстояние от оси вращения до центра масс груза (измеряется при выполнении работы). Теоретический момент инерции после суммирования вычисляется по формуле: I = I 0 + 4 m 1 l 2 + 4 m 2 l c2/3 (4.5)
Описание экспериментальной установки
Рис. 4.2 Внешний вид установки представлен на рис.4.2. Регулировочные винты 1 обеспечивают горизонтальную установку основания 2, к которому крепится вертикальная колонка 3, на которой нанесена миллиметровая шкала. К этой колонке прикреплены неподвижный кронштейн 4 и верхний подвижный 5, с помощью которого можно регулировать длину пути груза h. Через диск 6 перекинута нить 7, один конец которой прикреплен к шкиву 8, а на втором конце закреплены грузы 9. Кронштейн 11 снабжен резиновым амортизатором для ограничения движения грузов. Включение прибора производится нажатием клавиши «сеть» 12, обнуление миллисекундомера производится клавишей «сброс» 13, клавиша «пуск» 14 включает миллисекундомер. Время падения груза высвечивается на индикаторе 15.
Порядок выполнения работы 1. Включить установку в сеть. 2. Убедиться, что к нити прикреплен только один груз. 3. Намотать нить на шкив 8, а второй конец с грузом перекинуть через диск 6. Груз поднять на высоту h. Нижний край груза должен совпадать с чертой на корпусе верхнего фотодатчика. 4. Нажать кнопку «пуск» и отпустить груз без толчка. При этом запускается миллисекундомер. Записать отсчет в таблицу 4.1. 5. Нажать кнопку «сброс» и проверить, произошло ли обнуление измерителя. 6. Повторить измерение пять раз, занося значения времени падения в таблицу 4.1. 7. Последовательно увеличивая массу падающего груза, повторить п.п. 3-6. Таблица 4.1
8. Измерить высоту падения груза и длину стержня крестовины. Занести измеренные значения в таблицу 4.2. В эту же таблицу занести значения величин, указанные на установке. Таблица 4.2
9. Вычислить среднее значение времени падения для каждой массы груза и занести в таблицу 4.1. 10. По формуле (4.4) рассчитать значение момента инерции при каждой массе падающего груза, используя среднее время падения, и занести в таблицу 4.1. Ускорение свободного падения для Санкт-Петербурга g = (9,82 ± 0,01) м/с2. 11. Рассчитать среднее значение момента инерции и оценить абсолютную и относительную погрешность его определения. 12. По формуле (4.5) вычислить теоретическое значение момента инерции маятника. Сравнить с экспериментально полученным. 13. По формуле 14. По формуле Таблица 4.3
15. По данным таблицы 4.3 построить график зависимости углового ускорения от вращающего момента: ε = ε(М). 16. Сделать вывод, подтверждает ли характер зависимости углового ускорения от вращающего момента основной закон динамики вращательного движения. Определить возможные причины отклонения от теоретической зависимости. 17. Определить по графику среднее значение момента инерции маятника как котангенс угла наклона прямой к оси абсцисс. 18. Записать окончательные результаты работы: экспериментально полученное значение момента инерции с погрешностью, теоретическое значение момента инерции и величину момента инерции, вычисленную по графику зависимости ε = ε(М).
Контрольные вопросы 1. Дать определение момента силы относительно точки и относительно оси. 2. Дать определение момента импульса материальной точки относительно точки и относительно оси. 3. Чему равен момент импульса твердого тела относительно оси? 4. Каков физический смысл момента инерции? Как вычислить момент инерции твердого тела? 5. Провести аналогию между характеристиками поступательного и вращательного движения. 6. Указать на чертеже направление момента силы натяжения нити, действующей на шкив в данной работе.
Литература: [ 1, § 27, 31, 32]; [ 2, § 30, 33, 36]; [ 4, §4.1-4.3]; [ 5 ]. Лабораторная работа №5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 3644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

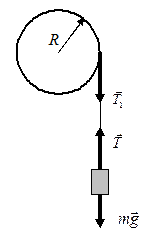
 .
.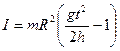 (4.4)
(4.4)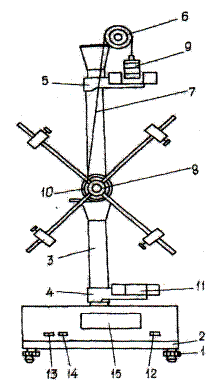
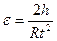 вычислить угловое ускорение для каждого груза. Вычисленные значения занести в таблицу 4.3.
вычислить угловое ускорение для каждого груза. Вычисленные значения занести в таблицу 4.3. вычислить значение вращающего момента для каждой массы груза. Вычисленные значения занести в таблицу 4.3.
вычислить значение вращающего момента для каждой массы груза. Вычисленные значения занести в таблицу 4.3.


