
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к обработкеСодержание книги Поиск на нашем сайте ВВЕДЕНИЕ
Физика – наука экспериментальная. Эксперимент есть источник познания и критерий истинности гипотез и теорий. С развитием науки и техники сфера эксперимента расширяется. В современных условиях физические методы исследования широко внедряются в различные отрасли техники. Поэтому очень важно уметь: проектировать эксперимент, пользоваться различными физическими приборами для измерений и компьютерными программами для обработки их результатов, критически оценивать неизбежные ошибки, возникающие при этом. Знания, умения и навыки, необходимые для проведения физического эксперимента, дает студенту физический практикум. Работа в лаборатории является неотъемлемой частью процесса изучения как физических законов и явлений, так и методов познания физики. Выполнение лабораторных работ аналогично проведению научного эксперимента с использованием стандартной методики состоит из похожих этапов
Подготовка к работе
Выполнению лабораторной работы предшествует самостоятельная подготовка, которая включает в себя: 1) изучение исследуемого физического явления; 2) вывод рабочей формулы; 3) уяснение используемой в данной работе методики измерений; 4) подготовка протокола лабораторной работы. Ознакомившись с порядком выполнения работы, следует продумать форму таблиц, в которые будут заноситься результаты эксперимента. Таблица должна иметь заглавие, в графах таблицы следует указать обозначение физической величины и единицы её измерения. Для величин, полученных многократными измерениями, удобно предусмотреть графы для записи отклонения каждого результата от среднего значения Кроме того, необходимо выбрать способ оценки погрешности результатов измерений (обычно в работе даются рекомендации по этому поводу). В результате протокол лабораторной работой должен содержать следующую информацию: § номер и название лабораторной работы (её номер в методичке); § фамилию и группу студента, выполняющего работу; § фамилии преподавателей. Обычно, эта информация размещается на стандартном титульном листе. Далее: § цель работы; § приборы и принадлежности; § схема установки с кратким описанием её частей; § расчётные формулы (в том числе, для расчёта погрешности косвенных измерений); § таблицы для занесения результатов измерений и вычислений; § ответы на контрольные вопросы, размещённые в конце каждой лабораторной работы, приводятся на отдельном листе написанными от руки. Иногда соответствующая теория к моменту выполнения лабораторной работы ещё не прочитана на лекциях, а, возможно, и вовсе не входит в программу лекционного курса, поэтому готовясь к работе, необходимо для ответов на контрольные вопросы пользоваться рекомендованной литературой. Протокол предъявляется преподавателю непосредственно перед лабораторной работой. Его наличие является неотъемлемой (но не единственной!) частью допуска к её выполнению. Проведение эксперимента
Проведение эксперимента – это центральный этап выполнения лабораторной работы. В лаборатории очень важно строго выполнять правила техники безопасности. Перед работой необходимо внимательно ознакомиться с установкой и приборами, изучить инструкцию, приложенную к ним. Приступать к проведению измерений можно, только получив допуск к работе. Для того чтобы число измерений было достаточным, полезно перед проведением основного эксперимента проводить серию предварительных измерений для ознакомления с работой приборов, характером изменения их показаний, необходимой плотностью экспериментальных точек на различных участках исследуемых зависимостей и т.п. Такое предварительное исследование позволит разумно выбрать число отдельных точек на различных участках, чтобы подробно исследовать места изгибов и максимумов кривой, не делая лишних измерений на участках ее плавного хода. Не забывайте следить за параметрами, которые в течение эксперимента должны оставаться постоянными (температура, давление, напряжение и т.п.). Результаты опыта должны быть записаны на бланке протокола так, чтобы эта запись была понятна не только ее автору. Записи должны быть сделаны авторучкой, применение карандаша недопустимо. Одним из распространенных способов представления результатов эксперимента являются графики. Строить их надо, выполняя следующие правила: § использовать только миллиметровую бумагу; § значение аргумента откладывать по оси абсцисс, по оси ординат – значение функции. § масштаб выбирать таким, чтобы он легко читался; § числовые значения на осях писать только для крупных единиц масштаба, делая записи ниже оси абсцисс и левее оси ординат; § строить только ту область функции, которая исследована на опыте; § не обозначать начало координат (точка 0), если это не имеет особого физического смысла; § наносить на график все полученные при измерениях значения; § проводить кривую плавно по усредненным значениям, избегая изломов. Строить график предпочтительнее «в реальном масштабе времени» (т. е. параллельно с ходом эксперимента), чем после полного его завершения. При таком подходе все особенности кривой и достоверность отдельных экспериментальных точек могут быть выявлены и учтены немедленно. Составление отчета
Отчёт является продолжением протокола, а, поэтому, должен содержать: § сводные таблицы с результатами измерений и необходимые графики; § подробный расчет искомых величин и их погрешностей; § окончательный результат с учетом оценки погрешностей измерений и вычислений; § анализ полученных результатов: сравнение экспериментального значения величины с ее табличным значением или согласование, полученной в результате опыта зависимости с той, что предсказывает теория. Составление отчета должно быть закончено до начала следующей лабораторной работы.
Защита лабораторной работы
Это последний, но не менее значительный этап работы. Необходимо учиться представлять самостоятельно выполненную работу. Для этого нужно уметь: § отвечать на вопросы по теоретической части работы; § пояснять методику проведения эксперимента; § пояснять выбранный способ обработки результатов; § анализировать полученные результаты и делать соответствующие выводы. Результатов измерений Измерением какой-либо физической величины называется операция, в результате которой мы узнаём, во сколько раз измеряемая величина больше (или меньше) соответствующей величины, принятой за единицу. Например, при измерении массы некоторого тела мы определяем, во сколько раз масса тела больше (или меньше), чем масса эталонного образца в 1 кг. Абсолютно точные измерения невозможны. Результат каждого измерения содержит ошибку, что связано как с принципиально ограниченной возможностью точности измерений, так и с природой измеряемых объектов. В задачу измерений входят не только нахождение величины, но и оценка допущенной при измерении погрешности. Ошибка измерений численно выражается разностью между значением, полученным при измерении, и истинным значением измеряемой величины. Истинным считается наиболее достоверное значение, определяемое специальными методиками. Абсолютная величина разности между истинным и измеренным значением физической величины, Полностью исключить или учесть ошибки невозможно, однако можно оценить степень доверия к полученному результату, т.е. ожидаемую повторяемость его при повторном измерении и указать вероятность пределов ошибок измерений. По характеру происхождения, по способам оценки ошибки измерений делят на три основных класса: § случайные ошибки, изменяющие величину и знак при повторении опыта; они обусловлены причинами, зависящими как от измерительного устройства, так и от внешних условий (температуры, плотности воздуха, напряжённости электрического и магнитного полей и т.п.); § систематические ошибки, которые при повторении опыта сохраняются постоянными или изменяются по определённому закону, связаны с ограниченной точностью приборов, с неправильным выбором метода измерения, неправильной установкой прибора, действием внешних факторов и др.; числовые значения измеряемых величин, содержащие систематические ошибки, иногда можно рассматривать как результаты измерений, выполненных с неправильно выбранным началом отсчёта; их можно исключить, когда они установлены; § грубые ошибки (промахи) возникают вследствие неисправности прибора, невнимательности экспериментатора, при нарушении условия проведения опыта. Эти погрешности легко выявляются, так как такие измерения заметно отличаются от остальных; их нужно исключить из рассмотрения. Измерения бывают: прямые – непосредственные измерения физических величин измерительными приборами (длина – линейкой, напряжение – вольтметром); косвенные – измерения физических величин, при которых необходимо использовать связь в виде формул с другими, непосредственно измеряемыми величинами (нахождение сопротивления проводника по показаниям вольтметра и амперметра и пр.). Ошибки косвенного измерения накапливаются из ошибок прямых измерений.
Пример расчёта погрешности прямых измерений
Проведены измерения действующего значения напряжения вольтметром с классом точности k = 1,0, цена деления шкалы c = 1 B, предел измерения D = 100 В. Получена следующая серия, состоящая из шести наблюдений.
В процессе измерений отсутствовали сильные электромагнитные наводки, внутреннее сопротивление вольтметра на несколько порядков больше сопротивления цепи, заключённой между точками, где измеряется падение потенциала. Можно считать, что постоянные систематические погрешности дают пренебрежимо малый вклад в результат наблюдений. Таким образом, серию результатов считаем исправленными результатами наблюдений. 1. Вычисляем среднее арифметическое (результат измерения):
2. Промахи в данной серии отсутствуют, так как максимальное отклонение от среднего второго значения (i = 2) превосходит среднюю абсолютную погрешность по разбросу (2) менее, чем в 2,5 раза:
3. Вычисляем среднее квадратичное отклонения результата измерений по формуле (3)
4. Определяем доверительные границы случайной погрешности (4) 5. Вычисляем систематическую погрешность, связанную с классом прибора (5a) 6. Вычисляем погрешность, связанную с округлением по шкале, принимая a = 1 (5б),
где b = 0,5,так как из таблицы результатов наблюдений видно, что отсчёт вёлся с точностью до 0,5 цены деления шкалы. Если округление результатов наблюдений не производилось, то 7. Определяем границу неисключённой систематической погрешности (5в) 8. 9. Сравниваем 10. 11. Таким образом, 0,8 < 12. Вычисляем суммарное среднее квадратичное отклонение результата измерения (6)
13. Вычисляем эмпирический коэффициент (7)
14. Граница погрешности результата измерения (8)
15. Записываем окончательный результат в стандартной форме:
Пример расчёта погрешности косвенного измерения Определить универсальную газовую постоянную по формуле
где t = 58oС, H = 919 мм рт. ст., тогда Формула (11) удобна для логарифмирования.
Прямым способ измерены давление Р и температура Т. Рабочую формулу для вычисления относительной погрешности получаем согласно (10):
Абсолютные погрешности
Вычислим
Запишем окончательный результат R = (8,24
Лабораторная работа № 1
Принцип работы прибора. Установка для изучения удара шаров схематически показана на рис. 1.1. Один из шаров отводится от положения равновесия на угол
где
где Аналогично определяется скорость второго шара после удара
где
Отсюда коэффициент восстановления
Таким образом, для определения коэффициента восстановления достаточно измерить углы Конкретные задания
1. Задавая различные углы отклонения первого шарика φ01, измерить углы φ2, на которые отклоняется после соударения второй шарик. Определить коэффициент восстановления при различных углах отклонения первого шарика. 2. Измерить время соударения шариков при тех же углах φ01. Вычислить силу взаимодействия шариков. 3. Исследовать зависимости времени и силы взаимодействия от относительной скорости шаров.
Порядок выполнения работы
1. Включить установку в сеть. 2. Установка 1. Нажать кнопку «сброс» и отвести шарик на угол φ01 = 10°. Нажать кнопку «пуск» и отпустить шарик без толчка. Установка 2. Установить стрелку электромагнита в положение, соответствующее углу φ01 = 4°. Нажать кнопку «сброс» и отвести шарик до соприкосновения с электромагнитом. 3. Нажать кнопку «пуск». 4. Зафиксировать максимальный угол отклонения φ2 второго шарика после соударения по шкале установки и записать его в таблицу 1.1, а также время соударения шариков, результат записать в таблицу 1.2. 5. Повторить измерение для данного угла φ01 пять раз. 6. Повторить измерения п.п. 2-4 для углов φ01: Установка 1: φ01 = 15˚, 20˚, 25˚, 30˚, 35˚, 40˚; Установка 2: φ01 = 6˚, 8˚, 10˚, 12˚, 14˚. Таблица 1.1
k ср=…..
Краткие сведения из теории
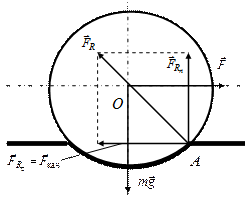
Всякое движущееся тело встречает сопротивление своему движению со стороны окружающей его среды и других тел, с которыми оно во время движения соприкасается. Иначе говоря, на любое движущееся тело действуют силы трения или силы сопротивления. В результате их действия всегда происходит превращение механической энергии во внутреннюю энергию трущихся тел, т.е. в энергию теплового движения их частиц. Силы трения имеют электромагнитную природу и связаны с межмолекулярным взаимодействием тел, но в механике останавливаются на эмпирических законах трения, которые зачастую являются довольно грубыми приближениями. Силы трения между взаимодействующими телами зависят не только от взаимного расположения, но и от их относительной скорости Остановимся на классификации сил трения. Трение называют внешним, если оно действует между различными соприкасающимися телами, не образующими единого тела (брусок на наклонной плоскости). Внутреннее трение проявляется между отдельными частями одного и того же тела (слои газа или жидкости). Трение между поверхностью твердого тела и жидкостью или газом, в котором оно движется, называют вязким. Трение между поверхностями твердых тел называют сухим. Оно делится на трение скольжения и трение качения. Сухое трение (в отличие от вязкого) не исчезает при обращении в ноль относительных скоростей соприкасающихся тел (трение покоя). Существует максимальное значение трения покоя f 0. Если брусок будет двигаться со скоростью v, то сила трения будет зависеть от скорости. Она не зависит тот площади поверхности контакта и пропорциональна силе нормального давления f n, с которой одно тело действует на другое. F тр = μ f n Коэффициент μ называют коэффициентом трения. Если речь идёт о трении скольжения, то μ – коэффициент трения скольжения. Трение качения возникает между шарообразным или цилиндрическим телом, катящимся без скольжения по плоской или изогнутой поверхности. Трение качения описывается теми же законами, что и трение скольжения, но коэффициент трения при качении во много раз меньше, чем при скольжении. Если тело катится без проскальзывания, то скорость точек касания поверхности равна нулю, а, значит, сила трения качения работы не совершает. Это справедливо, если при качении не возникают деформации, как самого тела, так и поверхности, по которой оно катится. Но при возникновении деформаций сила трения качения совершает отрицательную работу и кинетическая энергия тела уменьшается. Убыль этой энергии идет на преодоление сил трения. Рассмотрим перераспределение сил, действующих на катящееся тело при возникновении деформаций.
Рис. 2.1 При качении по плоской поверхности шара возникают деформации. Поэтому точка А приложения силы F R реакции поверхности несколько смещается вперед, а линия действия силы отклоняется от вертикали назад (рис.2.1). Нормальная составляющая реакции F R п = – mg, а касательная составляющая F Rτ и является силой качения: F кач = F Rτ. При равномерном качении сила F кач компенсируется силой тяги F, а реакция F R направлена вдоль прямой АО, так что ее момент относительно, оси симметрии катящегося тела равен нулю. Если R – радиус шара, а f к величина смещения точки А приложения реакции, то из условия равенства нулю момента силы относительно оси 0 следует, что F кач · R = F R п · f к = mg · f к. Поэтому для силы трения качения справедлив закон Кулона: F кач = f к · Величину f к называют коэффициентом трения качения k тр.
Принцип работы прибора Прибор предназначен для определения коэффициента трения качения. Наклоняем маятник на угол, для которого будем определять коэффициент трения качения, и отклоняем шарик от положения равновесия на угол 4-5º по лицевой шкале. После пуска шара он будет скатываться по образцу. Измеряется угол, на который отклоняется от положения равновесия шарик, после заданного числа колебаний. Коэффициент трения качения определяется по формуле
где R – радиус шара, мм; α 0 – угол начального отклонения маятника, рад; α n – угол, считанный после n полных колебаний маятника, рад; п – количество полных колебаний маятника; β – угол отклонения маятника от вертикали, прочитанный на боковой шкале.
Конкретные задания 1. Определить коэффициент трения качения. 2. Оценить погрешность полученного значения.
Порядок выполнения работы
1. Наклонить колонку 8 прибора (см. рис. 2.2) на угол β= 30°. 2. Отклонить шар от положения равновесия на угол α0 = 5° и отпустить. Шар начнёт совершать колебания. 3. Считать угол αnотклонения шарика после пяти полных колебаний. Результаты занести в таблицу 2.1. 4. Повторить действия п.п. 2,3 ещё четыре раза. 5. Выполнить измерения для углов β = 45°, 60°, повторяя действия п.п. 2-4. Таблица 2.1
* При подстановке в расчётную формулу деления следует перевести в радианы (см. инструкцию на установке).
Краткие сведения из теории
Рис. 3.1 Рассмотрим движение системы двух тел (т 1 и т 2), соединенных нитью, проходящей через блок массой тб и радиусом R (рис.3.1). Если предположить, что трение на оси блока отсутствует, а также пренебречь весом нити и силой сопротивления воздуха, то эта задача представляет собой идеализацию реальной экспериментальной установки данной работы. Для нахождения ускорения движения тел напишем законы поступательного движения тел и вращательного движения блока и решим их: а) II закон Ньютона для правого тела
б) II закон Ньютона для левого тела
в) закон динамики вращения блока
Здесь Решая совместно данную систему уравнений движения, получаем
Таким образом, грузы должны двигаться с постоянным ускорением. Известно, что при равноускоренном движении с нулевой начальной скоростью путь, пройденный телом по истечении времени t от начала движения, выражается формулой
Описанная ниже экспериментальная установка позволяет измерять время прохождения системой тел различных фиксированных расстояний. По этим данным можно определить величину ускорения грузов. Сначала следует убедиться в том, что движение имеет действительно равноускоренный характер. Предположим, что измерены время t 1, t 2, t 3, …прохождения системой тел расстояний S 1, S 2, S 3, …Полученные данные нужно представить на графике в виде зависимости 2 S (t 2). Если точки на графике достаточно хорошо укладываются на прямую линию, то это говорит о том, что ускорение движения в соответствии с формулой (3.1) имеет постоянную величину. По углу наклона прямой линии можно найти величину ускорения а. Располагая таким методом определения величины ускорения и изменяя в опытах величину перегрузки, можно исследовать зависимость ускорения тел от действующей на них силы. Изменяя массу тел, можно исследовать зависимость ускорения от массы тел.
Конкретные задачи
1. Определить ускорение движения системы тел. Убедиться, что движение является равноускоренным. 2. Исследовать зависимость ускорения системы от массы движущихся тел. 3. Исследовать зависимость ускорения системы от действующей на грузы силы. 4. Сделать вывод о соответствии полученных результатов законам динамики.
Порядок выполнения работы 1. Включить приборы в сеть. Установить груз I на столик 7 (рис. 3.2). По вертикальной шкале 3, снять начальную координату l' нижнего торца груза II, записать полученный результат. Снять нить с блока и установить на грузы I и II дополнительные грузы так, чтобы суммарная масса грузов стала равна 100 г и 70 г соответственно (с учётом начальной массы). Установить ограничитель 6 горизонтальным участком на отметке l 1 =35 см. Поместить систему грузов на блок так, чтобы груз II нижним торцом касался ограничителя. Придерживая его в таком положении, включить секундомер (на задней панели электронного блока), нить зафиксируется. Установка готова к работе. 2. Нажать кнопку «Пуск» электронного секундомера, при этом грузы придут в движение, и одновременно начнется отсчет времени. При прохождении груза I мимо фотоэлемента секундомер остановится. Записать показание секундомера в табл. 3.1. 3. Опустить груз II на ограничитель, придерживая его, нажать кнопки «Стоп» и «Сброс» (обращайте внимание на то, чтобы груз I не раскачивался). Записать показания секундомера. Выполнить аналогичные измерения ещё два раза. Результаты занести в таблицу 3.1, в колонку, соответствующую S 1, где S 1 = l 1 – l' – 4,2, см (грузы I и II проходят равные расстояния l 1 – l', однако,секундомер фиксирует время, за которое груз I проходит расстояние на 4,2 см меньше с учётом расстояния от столика 7 до датчика фотоэлемента 2). l' = …….., см т 1 = 100 г т 2 = 70 г Таблица 3.1.
4. Перемещая ограничитель, провести аналогичные операция для li = 30, 25 и 20 см, заполнив табл. 3.1, где Si = li – l' – 4,2, см. Эти данные позволят определить величину ускорения а для данной массы грузов, а также сделать вывод о характере их движения. 5. Установить ограничитель на отметке l = 35 см. 6. Снять нить с блока и установить дополнительные грузы так, чтобы суммарная масса I и II грузов были равны 60 и 50 г соответственно. 7. Измерить время движения грузов 5 раз. Результаты занести в таблицу 3.2. 8. Провести серию измерений, повторив п.п. 5, 6, когда массы грузов составляют 70 и 60, 80 и 70, 90 и 80, 100 и 90 г. Результаты занести в таблицу 3.2. S = l – l' – 4,2 = 20,8 – l' = ………., смТаблица 3.2
9. Изменяя величину перегрузки, исследовать зависимость ускорения системы от действующей на грузы силы. Для этого проделать аналогичные испытания, когда массы грузов составляют 120 и 50, 110 и 60, 100 и 70, 90 и 80 г. Высоту, на которой находится ограничитель оставить прежней. Результаты занести в таблицу 3.3. S = l – l' – 4,2 = 20,8 – l' = ………, смТаблица 3.3
Краткие сведения из теории Основной закон вращательного движения твердого тела описывается уравнением Учитывая, что L z = I ω, где I − момент инерции тела относительно этой оси, ω − угловая скорость вращения тела и I ε = М z Записанный в такой форме закон аналогичен второму закону Ньютона для поступательного движения:
Момента инерции.
Момент инерции является аддитивной величиной, то есть момент инерции системы тел равен сумме моментов инерции всех тел, входящих в систему. Маятник Обербека состоит из шкива (включая ось и втулку крестовины), четырех стержней крестовины и грузов, укрепленных на крестовине. Момент инерции шкива указан на установке. Момент инерции стержня относительно оси, проходящей через его конец, равен m 2 l c2/3, где m 2 − масса стержня без груза, l c − длина стержня крестовины − указаны на установке. Грузы, укрепленные на крестовине, приближенно можно считать за точечные массы. Тогда момент инерции каждого груза равен m 1 |

 и для квадратов этих отклонений
и для квадратов этих отклонений  , что удобно для вычисления случайной погрешности измерения.
, что удобно для вычисления случайной погрешности измерения. называется абсолютной ошибкой. Ошибка измерений, выраженная в долях или процентах от истинного значения измеряемой величины,
называется абсолютной ошибкой. Ошибка измерений, выраженная в долях или процентах от истинного значения измеряемой величины,  называется относительной ошибкой.
называется относительной ошибкой.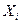 , B
, B
 , B
, B
 , B2
, B2

 B
B ,
, 
 В.
В. = 2,57×0,302 = 0,78 B.
= 2,57×0,302 = 0,78 B. = 1,0 B.
= 1,0 B. B,
B, = 0.
= 0. B
B и
и  :
: = 1,23/0,302 = 4,1.
= 1,23/0,302 = 4,1. B
B
 0,502 B.
0,502 B. B,
B,  = 0,95.
= 0,95. , (11)
, (11) =
=  кг/моль;
кг/моль;  = 1,3 кг/м3; Т = t + 273, К, t – температура, измеряемая с помощью термометра (цена деления 1oС); Р = H · 133, Па, H – давление, измеряемое в мм рт. ст. (цена деления 1 мм). В результате измерения мы получили:
= 1,3 кг/м3; Т = t + 273, К, t – температура, измеряемая с помощью термометра (цена деления 1oС); Р = H · 133, Па, H – давление, измеряемое в мм рт. ст. (цена деления 1 мм). В результате измерения мы получили: .
.
 .
. и
и  определяем в данном случае как погрешность, связанную с округлением по шкале прибора (5б). При доверительной вероятности
определяем в данном случае как погрешность, связанную с округлением по шкале прибора (5б). При доверительной вероятности  мм рт. ст.;
мм рт. ст.;  K.
K. , тогда
, тогда Дж/моль·К.
Дж/моль·К.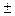 0,07) Дж/моль·К (
0,07) Дж/моль·К (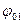 и отпускается. Из закона сохранения механической энергии следует
и отпускается. Из закона сохранения механической энергии следует ,
, – скорость ударяющего шара до удара. Из рисунка видно, что высота шара в начальном положении
– скорость ударяющего шара до удара. Из рисунка видно, что высота шара в начальном положении  . Отсюда
. Отсюда , (1.16)
, (1.16) – ускорение свободного падения;
– ускорение свободного падения;  – длина подвески шаров;
– длина подвески шаров;  ,
, угол, на который отклоняется второй шар после удара. При
угол, на который отклоняется второй шар после удара. При  и
и  из формулы (1.13) находим:
из формулы (1.13) находим: .
. (1.17)
(1.17)

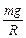 .
. . (2.1)
. (2.1)

 ;
; ;
;
 – момент инерции блока, ε – угловое ускорение вращения блока, связанное с ускорением движущихся грузов (при условии, что нить в блоке не проскальзывает) соотношением
– момент инерции блока, ε – угловое ускорение вращения блока, связанное с ускорением движущихся грузов (при условии, что нить в блоке не проскальзывает) соотношением  , а
, а  - момент сил, действующих на блок.
- момент сил, действующих на блок. . (3.1)
. (3.1) . (3.2)
. (3.2) =с2
=с2
 =с2
=с2
 =с2
=с2
 =с2
=с2
 ср, мс2
ср, мс2
 , где
, где  − момент импульса тела относительно некоторой точки,
− момент импульса тела относительно некоторой точки,  − суммарный момент всех внешних сил, действующих на тело, относительно этой же точки. При вращении относительно неподвижной оси z основной закон вращательного движения принимает вид:
− суммарный момент всех внешних сил, действующих на тело, относительно этой же точки. При вращении относительно неподвижной оси z основной закон вращательного движения принимает вид: 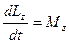 , где L z и M z − проекции момента импульса и равнодействующей силы на ось z.
, где L z и M z − проекции момента импульса и равнодействующей силы на ось z. − угловое ускорение, получаем основной закон динамики вращательного движения относительно неподвижной оси в виде:
− угловое ускорение, получаем основной закон динамики вращательного движения относительно неподвижной оси в виде: . Аналогом массы является момент инерции, аналогом линейного ускорения − угловое ускорение и аналогом силы − момент силы.
. Аналогом массы является момент инерции, аналогом линейного ускорения − угловое ускорение и аналогом силы − момент силы.


